今回はオイラー定数と呼ばれるものが入試の背景にある問題を選びました. 私がこのオイラー定数と初めて出会ったのは数学検定1級の勉強をしているときです. 「数学検定1級実践演習」に掲載されている過去問の解説の中に出てきました. 最後にこの問題についても紹介したいと思います.
問題文全文
\(n\) は自然数とし,
\begin{align}a_n=\left(1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}\right)-\log n\end{align}
とおく. \(\displaystyle y=\frac{1}{x}\left(x>0\right)\) のグラフと, \(\displaystyle \int \frac{1}{x}dx\) を考えることにより, 数列 \(a_1, a_2, \cdots , a_n, \cdots\) の性質を調べる.
(1) \(\displaystyle a_n>\frac{1}{n}\left(n\geqq 2\right)\) を証明せよ.
(2) \(a_n>a_{n+1}\) を証明せよ.
(3) \(\displaystyle y=\frac{1}{x}\left(x>0\right)\) のグラフが下に凸であることを用いて,
\begin{align}\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)>\log (n+1)-\log n\end{align}
を証明せよ.
(4) \(\displaystyle a_n>\frac{1}{2}+\frac{1}{2n}\left(n\geqq 2\right)\) を証明せよ.
(1)の着眼点
① \(a_n\) は \(\displaystyle \frac{1}{k}\left(k=1, 2, \cdots, n\right)\) の和の形で与えられており, さらに不等式を証明せよということなので, \(\displaystyle y=\frac{1}{x}\) のグラフを利用した面積比較による証明になります. 今回は問題が親切なので教えてくれていますが, このヒントがなくてもできなければいけません.
② 面積比較による証明では \(\sum\) 計算をすることが多いです. その際
\begin{align}\displaystyle \int_1^n=\int_1^2+\int_2^3+\cdots +\int_{n-1}^n=\sum_{k=1}^{n-1}\int_k^{k+1}\end{align}
のように積分区間をつなぎ合わせることがポイントです.
(1)の解答
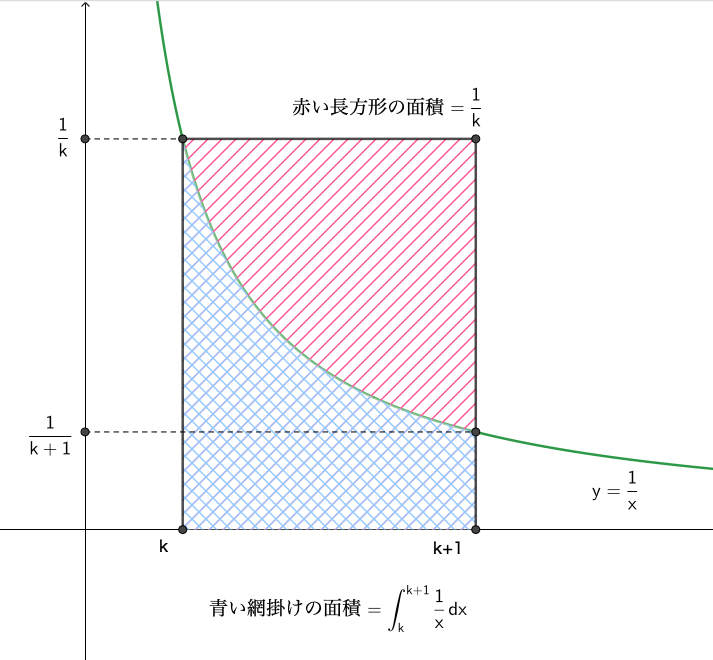
図より,
\begin{align}\frac{1}{k}>\int_k^{k+1}\frac{1}{x}dx\end{align}
\begin{align}\sum_{k=1}^{n-1}\frac{1}{k}>\sum_{k=1}^{n-1}\int_k^{k+1}\frac{1}{x}dx\end{align}
\begin{align}\displaystyle 1+\frac{1}{2}+\cdots +\frac{1}{n-1}>\int_1^n \frac{1}{x}dx\end{align}
ここで, \(\displaystyle \int_1^n \frac{1}{x}dx =\biggr[ \log x\bigg]_1^n=\log n\) であるから,
\begin{align}\displaystyle 1+\frac{1}{2}+\cdots +\frac{1}{n-1}+\frac{1}{n}>\log n+\frac{1}{n}\end{align}
したがって, \(\displaystyle a_n>\frac{1}{n}\).
(2)の着眼点
「 \(a_n>a_{n+1}\) を証明せよ. 」と書いて「単調減少であることを証明せよ。」と読みます。数列においてはこう読めることが重要です。
単調減少(増加)の証明は「引いて0より小さい(大きい)」を示せばよいことが多いです。他には関数 \(f(x)\) として微分することも考えられます。(実数値関数として示せれば, 当然自然数のときも成り立つからです.)
もし, 式に階乗や累乗根などが含まれている場合は \(\displaystyle \frac{a_n}{a_{n+1}}>1\) を示すという方法も考えられます.(確率漸化式などでよく出てくる手法です. 大学数学でいえば収束半径を求めるときのダランベールの判定をするときに出てきます.)
(2)の解答
\begin{align}a_n-a_{n+1}=\left(1+\frac{1}{2}+\cdots +\frac{1}{n}\right)-\log n -\left\{\left( 1+\frac{1}{2}+\cdots +\frac{1}{n} +\frac{1}{n+1}\right)-\log (n+1)\right\}\end{align}
\begin{align}=\log (n+1)-\log n -\frac{1}{n+1}=\log \frac{n+1}{n}-\frac{1}{n+1}\end{align}
ここで, \(\displaystyle f(x)=\log \frac{x+1}{x}-\frac{1}{x+1}\left(x\geqq 1\right) \) とおく.
\begin{align}f^{\prime}(x)=\frac{x}{x+1}\times\left(-\frac{1}{x^2}\right)+\frac{1}{(x+1)^2}\end{align}
\begin{align}=-\frac{1}{x(x+1)}+\frac{1}{(x+1)^2}\end{align}
\begin{align}=\frac{-(x+1)+x}{x(x+1)^2}=-\frac{1}{x(x+1)^2}<0\end{align}
よって, \(f(x)\) は \(x\geqq 1\) において単調減少.
また, \(\displaystyle \lim_{x\rightarrow \infty}f(x)=0\) であることと合わせると, \(f(x)\) は\(x\geqq 1\) において \(f(x)>0\) となる.
したがって, \(a_n>a_{n+1}\) が示された.
(3)の着眼点
① グラフが下に凸であることを利用してとあるのでやはり面積比較でしょう. 図を丁寧にかくと直角三角形の面積の方が積分計算よりも大きいことがわかるのでこれを利用します.
② もし, このヒントがなければ, 右辺の形から \(g(x)=\log x\) とおいて平均値の定理を使うことを考えたくなります.(少しやってみましたがうまくいきませんでした.)平均値の定理も不等式証明には強力な道具です.
(3)の解答
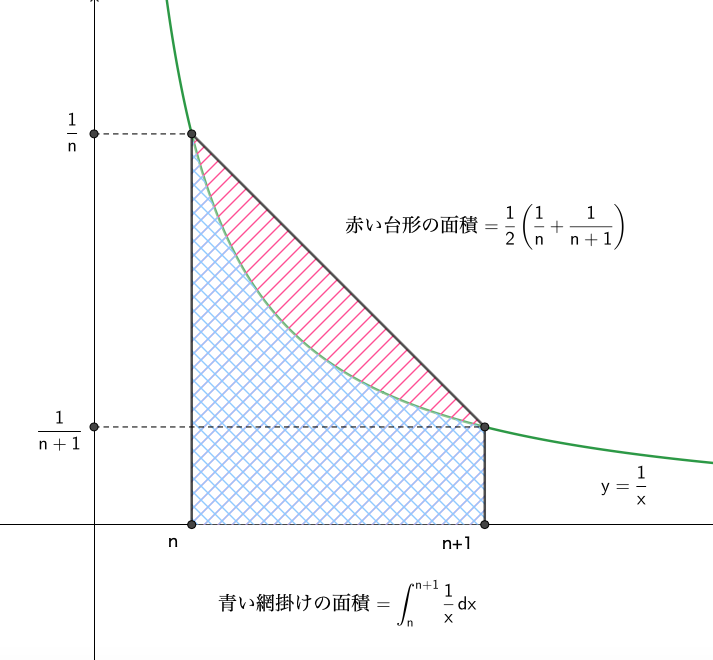
上図より, \(n\leqq x\leqq n+1\) において,
\begin{align}\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right) >\int_n^{n+1}\frac{1}{x}dx \end{align}
\begin{align}\int_n^{n+1}\frac{1}{x}dx =\biggl[\log x\biggr]_n^{n+1}=\log (n+1)-\log n\end{align}
より,
\begin{align}\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n+1}\right)>\log (n+1)-\log n\end{align}
(4)の着眼点
① 問題の流れとして (3) を使うことになるはずです. (3) の式を観察してみると, 右辺が (2) で計算した \(\displaystyle a_n-a_{n+1}=\log (n+1)-\log n -\frac{1}{n+1}\) に近い形をしています. まずは (3) の不等式から \(\displaystyle \frac{1}{n+1}\) を引いてみてまた考察することにします.
② ①をやってみると以下の式を得ます.
\begin{align}\frac{1}{2}\left(\frac{1}{n}-\frac{1}{n+1}\right)>a_n-a_{n+1}\end{align}
この式は両辺とも「1個違いの差」の形になっています.より一般的に言えば \(f(n)-f(n+1)\) の形になっています. このような形の時は和をとることで初項と末項だけが残る形にできます.
\begin{align}\sum_{k=1}^n\left\{f(k)-f(k+1)\right\}=f(1)-f(n+1)\end{align}
これを利用して計算をしてみます.今回の問題ではこれでゴールまでいけます.
(4)の解答
(3) の不等式の両辺から \(\displaystyle \frac{1}{n+1}\) を引くと
\begin{align}\frac{1}{2}\left(\frac{1}{n}-\frac{1}{n+1}\right)>a_n-a_{n+1}\end{align}
\begin{align}\sum_{k=1}^{n-1}\frac{1}{2}\left(\frac{1}{k}-\frac{1}{k+1}\right)>\sum_{k=1}^{n-1}\left(a_k-a_{k+1}\right)\end{align}
\begin{align}\frac{1}{2}\left(1-\frac{1}{n}\right)>a_1-a_n\end{align}
\(a_1=1\) であるから,
\begin{align}a_n>1-\frac{1}{2}\left(1-\frac{1}{n}\right)=\frac{1}{2}+\frac{1}{2n}.\end{align}
発展 オイラー定数について
この問題をもう少し考察してみます. (2) で単調減少であることを証明しました. そして (4) の不等式から数列 \({a_n}\) はすべての自然数 \(n\) に対して, \(\displaystyle \frac{1}{2}\) より大きいことから下に有界であることが分かります.
一般的に下に(上に)有界な単調減少(増加)数列は収束することが知られています. この問題の場合は 0.5772156649くらいの値に収束することが知られていてこれをオイラー定数と呼び, \(\gamma\) で表すそうです. すなわち
\begin{align}\gamma=\lim_{n\rightarrow \infty}\left(\sum_{k=1}^n\frac{1}{k}-\log n\right)\end{align}
で表される定数で, よく知られているように \(\displaystyle \lim_{n\rightarrow \infty}\sum_{k=1}^n\frac{1}{k}\) は発散しますが, そのスピードが対数関数並みにかなりゆっくりであることが分かります.
オイラー定数 \(\gamma\) は 有理数か無理数かさえまだ知られていない不思議な数です.
オイラー定数は数学検定1級でも出題された
(数学検定1級過去問より)次の極限値を求めなさい. $$\displaystyle \lim_{n\rightarrow \infty}\left(\log_{e}n\right)^{-1}\cdot \sum_{k=1}^n\frac{{}_n\mathrm{C}_k(-1)^{k+1}}{k}$$
\begin{align}\sum_{k=1}^n\frac{{}_n\mathrm{C}_k(-1)^{k+1}}{k}=n-\frac{1}{2} {}_n\mathrm{C}_2+\frac{1}{3} {}_n\mathrm{C}_3-\frac{1}{4} {}_n\mathrm{C}_4+\cdots +\frac{(-1)^{n+1}}{n}\end{align}
\(\displaystyle f(x)=\sum_{k=1}^n\frac{{}_n\mathrm{C}_k(-1)^{k+1}x^k}{k}\) とおくと,
\begin{align}f^{\prime}(x)=\sum_{k=1}^n{}_n\mathrm{C}_k(-1)^{k+1}x^{k-1}\end{align}
\begin{align}=\sum_{k=1}^n{}_n\mathrm{C}_k(-1)^{k-1}x^{k-1}=\sum_{k=1}^n{}_n\mathrm{C}_k(-x)^{k-1}\end{align}
\begin{align}=-\frac{1}{x}\sum_{k=1}^n{}_n\mathrm{C}_k(-x)^k=-\frac{1}{x}\left\{\sum_{k=0}^n{}_n\mathrm{C}_k(-x)^k-1\right\}\end{align}
\begin{align}=\frac{1-\sum_{k=0}^n{}_n\mathrm{C}_k(-x)^k}{x}=\frac{1-(1-x)^n}{x}\end{align}
最後の等号は二項定理を利用した. \(f(0)=0\) から,
\begin{align}f(1)=\int_0^1 f^{\prime}(x)dx=\int_0^1\frac{1-(1-x)^n}{x}dx\end{align}
\(x=1-t\) とおくと,
\begin{align} \int_0^1\frac{1-(1-x)^n}{x}dx =\int_0^1\frac{1-t^n}{1-t}\end{align}
\begin{align}=\int_0^1\left(1+t+t^2+\cdots +t^{n-1}\right)dt=1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}\end{align}
\begin{align}\lim_{n\rightarrow \infty}\left(1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}-\log n\right)=\gamma\end{align}
であることに注意すると, \(n\rightarrow \infty\) のとき
\begin{align}f(1)=\sum_{k=1}^n\frac{{}_n\mathrm{C}_k(-1)^{k+1}}{k}= 1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n} \rightarrow \log_e n+\gamma\end{align}
となる. したがって,
\begin{align} \lim_{n\rightarrow \infty}\left(\log_{e}n\right)^{-1}\cdot \sum_{k=1}^n\frac{{}_n\mathrm{C}_k(-1)^{k+1}}{k} \end{align}
\begin{align}=\lim_{n\rightarrow \infty}\frac{\log_e n+\gamma}{\log_e n}=\lim_{n\rightarrow \infty} \left(1+\frac{\gamma}{\log_e n}\right)=1.\end{align}





