２月２日（火）から2021年の理科大一般選抜が始まりました. 初日は経営学部でした. 受験された方はお疲れ様でした. まずは経営学部受験者全員が解答する２回目の問題の解説を行います. 問題を提供していただいたものについては出来るだけ早く解説をしていきたいと思っていますので情報提供お待ちしております.
微積分以外の解答も手書きではありますが\(,\) twitterにあげていますのでよろしければ下のリンクからご覧ください.
※２月４日０：３０追記 ３日の理工学部の手書き解答速報もtwitterにアップしていますのでよろしければご覧ください.
解答にもし何らかのミスがあった場合はコメントまたはtwitter（@tusbiseki）でご指摘いただければと思います.
問題文全文
実数 \(x,~y\) が\(,\) \(1\leqq x\leqq 4,~y\geqq 1,\) および\(,\) \(x^2-x=y^2+y\) を満たす. このとき\(,\) \(4x^3-9y^3\) の最大値は \(\fbox{$\hskip0.8emシス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) であり\(,\) 最小値は \(\fbox{$\hskip0.8emセソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である.
着眼点
\(x,~y\) の \(3\) 次式の最大最小を求める問題です. \(2\) 変数関数の最大最小問題は以下の\(2\) パターンがあります.
① \(x\) と \(y\) が独立に動いている場合
→片方を定数化（\(y\) を定数化したとします.）して \(x\) だけの \(1\) 変数関数としてまず最大値（最小値）を求める. （\(y\) の式で表されます.）
→次に \(y\) を動かして最大値（最小値）を求める.
と一つずつ処理していくことになります. （予選決勝法と呼ばれます.）
② \(x\) と \(y\) が従属の関係にある場合（\(x\) と \(y\) の関係式が与えられている場合）
→片方を消去して \(1\) 変数関数とします. このとき\(,\) 定義域に細心の注意を払います.
例えば\(,\) \(x^2+y^2=1\) という関係式が与えられている場合は\(,\) \(y^2=1-x^2\geqq 0\) より\(,\) \(-1\leqq x\leqq 1\) という定義域のもと考える必要があります. 見落としがちなので要注意です.
今回は \(x\) と \(y\) の関係式が与えられているので\(,\) 一文字消去できないかを考えましょう.
解答
より\(,\)
\(y=-x\) であるとすると\(,\) \(1\leqq x\leqq 4\) より \(-4\leqq y\leqq -1\) であるが\(,\) これは \(y\geqq 1\) であることに反する. よって\(,\) \(y=x-1\).
\(y\geqq 1\) より\(,\) \(y=x-1\geqq 1\) つまり\(,\) \(x\geqq 2\) であるから\(,\) \(2\leqq x\leqq 4\).
このとき\(,\)
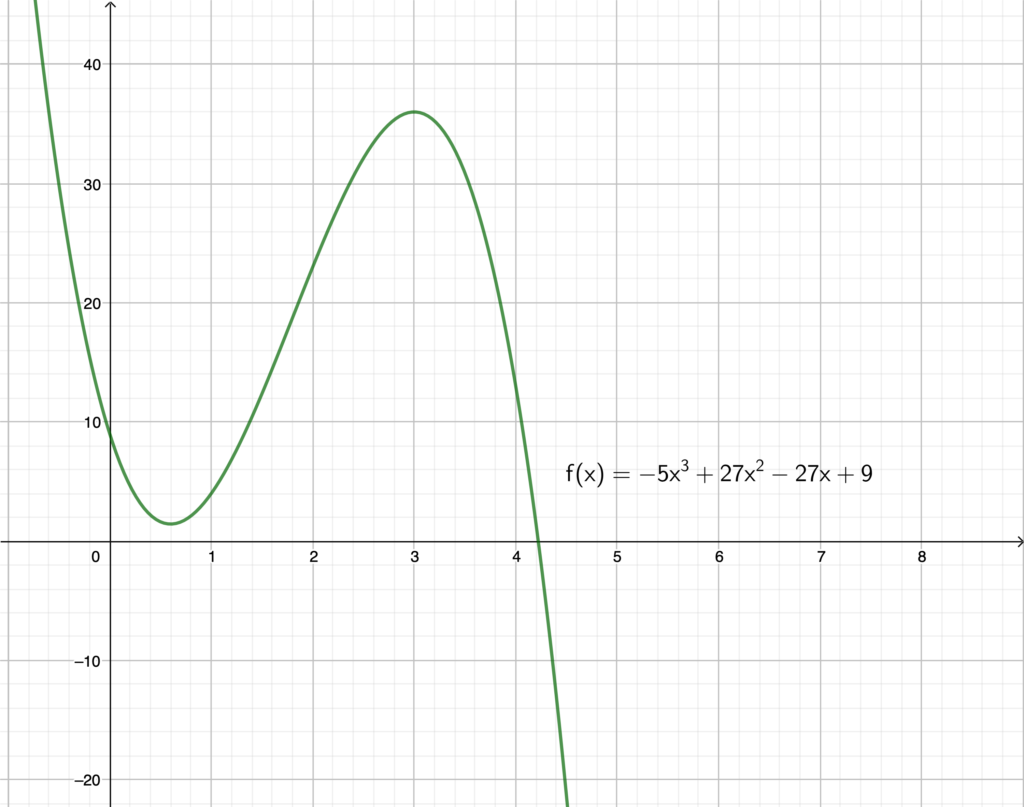
\(f(x)=-5x^3+27x^2-27x+9\) とおく. \((2\leqq x\leqq 4)\)
よって\(,\) 増減表は以下のようになる.
\begin{array}{c|c|c|c|c|c}x & 2 & \cdots & 3 & \cdots & 4 \\ \hline f^{\prime}(x) & {} & + & 0 & – & {} \\ \hline f(x) & 23 & \nearrow & 36 & \searrow & 13\\ \end{array}
\(f(2),~f(3),~f(4)\) を計算するときは\(,\) \(-5x^3+27x^2-27x+9\) の方ではなく\(,\) \(4x^3-9(x-1)^3\) の方に代入する方が遥かに楽です.
増減表より\(,\)
\(x=3\) のとき\(,\) 最大値 \(36\)\(,\) \(x=4\) のとき\(,\) 最小値 \(13\).
※参考として \(y=f(x)\) のグラフは以下のようになります.
コメント