問題文全文 \(k\) を \(0\) 以上の実数とする. 座標平面において\(,\) 放物線 \(C_1~:~y=-6x^2+kx\) と放物線 \(C_2~:~y=6x^2+3\) を考える.
(1) 放物線 \(C_1\) と放物線 \(C_2\) の両方に接する異なる直線が \(2\) 本存在するような定数 \(k\) の値の範囲は\(,\) \(0\leqq k <\fbox{$\hskip0.8emアイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である.
(2) \(k\) が \(0\leqq k <\fbox{$\hskip0.8emアイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) の範囲を動くとき\(,\) 放物線 \(C_1\) と放物線 \(C_2\) の両方に接する \(2\) 本の直線を \({\ell}_1,~{\ell}_2\) とし\(,\) 直線 \({\ell}_1\) と直線 \({\ell}_2\) の交点を \(\mathrm{P}\) とする. ここで\(,\) 直線 \({\ell}_1\) の傾きは直線 \({\ell}_2\) の傾きよりも大きいとする.
(a) 点 \(\mathrm{P}\) の \(x\) 座標の範囲は
\begin{align}\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\leqq x < \frac{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
であり\(,\) 点 \(\mathrm{P}\) は曲線
\begin{align}y=\fbox{$\hskip0.8emカキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~x^{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}+\frac{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
上の点である.
(b) 直線 \({\ell}_1\) が原点 \(\mathrm{O}\) を通るとき\(,\)
\begin{align}k=\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}~\sqrt{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
である. またこのとき\(,\) \(2\) 直線 \({\ell}_1,~{\ell}_2,\) および放物線 \(C_1\) で囲まれた部分を\(,\) \(x\) 軸の周りに \(1\) 回転させてできる立体の体積は
\begin{align}\frac{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}} ~\sqrt{\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}~\pi\end{align}
である.
共通接線の求め方 一般に曲線 \(C,~C^{\prime}\) の両方に接する直線を共通接線 といいます. 共通接線の問題は\(,\) 「接点を共有する場合」と「接点を共有しない場合」があります.
今回は「接点を共有しない場合」になります. 接点を共有しない場合の共通接線の求め方は以下の \(2\) 通りがあります.
①(万能な解法)\(C,~C^{\prime}\) における接点の \(x\) 座標をそれぞれ \(s,~t\) とおき\(,\) \(C\) における接線を \(s\) を用いて表し\(,\) \(C^{\prime}\) における接線を \(t\) を用いて表す. これらがともに同じ直線を表すので「傾き」と「切片」が等しいことを式にする.
②(\(C,~C^{\prime}\) のいずれかが二次曲線の場合のみの解法)
\(C\) を二次曲線\(,\) \(C^{\prime}\) を一般の曲線(二次曲線でも良い)とする.
\(C^{\prime}\) における接点の \(x\) 座標を \(t\) とおいて\(,\) 接線の方程式を \(t\) を用いて表す.
この直線は \(C\) と接するので\(,\) \(C\) と接線の方程式を連立する.
二次曲線と連立しているので2次方程式が出てくる.
接するので判別式\(D=0\) を解くことで求められる.
(1) の着眼点 今回は \(C_1,~C_2\) ともに二次曲線です. 上記の②の解法を選びます.
\(C_2\) には文字が含まれていないので\(,\) \(C_1\) で作るよりも接線の方程式が簡単になります.
\(C_2\) における接点の \(x\) 座標を \(t\) とおくと\(,\) 接線の方程式が \(t\) を用いて表されます.
接線の方程式と \(C_1\) を連立すると \(t,~k\) を含む \(x\) の \(2\) 次方程式になります.
この \(2\) 次方程式の判別式\(=0\) を解きましょう.
(1) の解答(②による解法) \(C_2\) について\(,\)
\begin{align}y^{\prime}=12x\end{align}
\(C_2\) における接点を \((t,~6t^2+3)\) とおくと\(,\) 接線の方程式は
\begin{align}y=12t(x-t)+6t^2+3\end{align}
\begin{align}y=12tx-6t^2+3\end{align}
これが \(C_1\) と接するから\(,\)
\begin{align}-6x^2+kx=12tx-6t^2+3\end{align}
\begin{align}6x^2+(12t-k)x-6t^2+3=0\end{align}
の判別式 \(D_1\) が\(D_1=0\) となる.
\begin{align}D_1=(12t-k)^2-4\cdot 6\cdot (-6t^2+3)=0\end{align}
\begin{align}288t^2-24kt+k^2-72=0~~~~\cdots ☆\end{align}
この \(t\) に関する \(2\) 次方程式が異なる \(2\) 解をもてばよいので \(,\) 判別式を \(D_2\) とおくと\(,\) \(D_2>0\) となる.
quandle
異なる \(2\) 本の共通接線をもつということは\(,\) 異なる \(2\) つの接点をもつということです.
\begin{align}\frac{D_2}{4}=(-12k)^2-288(k^2-72)>0\end{align}
\begin{align}144k^2<288\cdot 72\end{align}
\begin{align}k^2<144\end{align}
\(k\geqq 0\) より\(,\)
\begin{align}0\leqq k <12~~~~\cdots \fbox{答}\end{align}
ア:1 イ:2
(1) の別解(①による解法) \(C_1\) における接点を \((s,~-6s^2+ks),\) \(C_2\) における接点を \((t,~6t^2+3)\) とおく.
\(C_1\) における接線は \(y^{\prime}=-12x\) より\(,\)
\begin{align}y=-12s(x-s)-6s^2+ks\end{align}
\begin{align}y=-12sx+6s^2+ks~~~~\cdots ③\end{align}
\(C_2\) における接線は \(y^{\prime}=12x\) より
\begin{align}y=12t(x-t)+6t^2+3\end{align}
\begin{align}y=12tx-6t^2+3~~~~\cdots ④\end{align}
③\(,\) ④は一致するので
\begin{align}\left\{\begin{array}{c}-12s=12t \\ 6s^2+ks=-6t^2+3\end{array}\right. \end{align}
\(t=-s\) より\(,\)
\begin{align}6s^2+ks=-6s^2+3\end{align}
\begin{align}12s^2+ks-3=0\end{align}
これが異なる \(2\) 解をもつので\(,\) 判別式を \(D\) とおくと\(,\) \(D>0\) となる.
\begin{align}D=k^2-4\cdot 12\cdot (-3)>0\end{align}
\begin{align}(k-12)(k+12)>0\end{align}
\(k\geqq 0\) より\(,\)
\begin{align}0\leqq k <12\end{align}
(2) (a) の着眼点 \({\ell}_1\) と \({\ell}_2\) はどちらも放物線 \(C_2\) の接線です.
一般に放物線に接する異なる \(2\) 本の接線の交点の \(x\) 座標は\(,\) \(2\) つの接点の \(x\) 座標の平均になることが知られています. 特に穴埋め形式の問題では威力を発揮する性質ですので覚えておきましょう.
詳しくは以下の記事にまとめていますので合わせて御覧ください.
(2) (a) の解答 \(C_2\) における \({\ell}_1,~{\ell}_2\) の接点の \(x\) 座標をそれぞれ \(x=\alpha ,~\beta~(\alpha > \beta )\) とおく. 解と係数の関係より\(,\)
\begin{align}\alpha +\beta =\frac{24k}{288}=\frac{k}{12},~\alpha \beta=\frac{k^2-72}{288}\end{align}
点 \(\mathrm{P}\) の \(x\) 座標は \(\displaystyle \frac{\alpha +\beta}{2}\) なので\(,\)
\begin{align}\frac{\alpha +\beta}{2}=\frac{k}{24}\end{align}
\(0\leqq k < 12\) より\(,\)
\begin{align}0\leqq \frac{k}{24}<\frac{1}{2}~~~~\cdots \fbox{答}\end{align}
点 \(\mathrm{P}\) は \({\ell}_1\) 上の点であるから\(,\)
\begin{align}{\ell}_1~:~y=12\alpha x-6{\alpha}^2+3\end{align}
に \(\displaystyle x=\frac{\alpha +\beta}{2}\) を代入して\(,\)
\begin{align}y=12\alpha \cdot \frac{\alpha +\beta}{2}-6{\alpha}^2+3\end{align}
\begin{align}=6\alpha \beta +3=\frac{k^2-72}{48}+3\end{align}
\(\mathrm{P}(X,~Y)\) とおくと
\begin{align}\left\{\begin{array}{c} \displaystyle X=\frac{k}{24} \\ \displaystyle Y=\frac{k^2-72}{48}+3\end{array}\right.\end{align}
\(k=24X\) より\(,\)
\begin{align}Y=\frac{(24X)^2-72}{48}+3=12X^2+\frac{3}{2}\end{align}
よって\(,\) 点 \(\mathrm{P}\) は
\begin{align}y=12x^2+\frac{3}{2}~~~~\cdots \fbox{答}\end{align}
上の点である.
quandle
今回は穴埋め形式なのでこの解答が一番速いと思います. 記述式でこの答案を出すのは避けたほうがいいかもしれません. 中点になるというのが使っていいか微妙なところだからです.
ウ:0 エ:1 オ:2 カ:1 キ:2 ク:2 ケ:3 コ:2
(2) (b) の解答 \(y=12tx-6t^2+3\) が原点を通るから\(,\)
\begin{align}0=-6t^2+3\end{align}
\begin{align}t=\frac{\sqrt{2}}{2}\end{align}
\begin{align}{\ell}_1~:~y=6\sqrt{2}x\end{align}
これが \(C_1\) と接するので\(,\)
\begin{align}-6x^2+kx=6\sqrt{2}x\end{align}
\begin{align}6x^2+(6\sqrt{2}-k)x=0\end{align}
\begin{align}x(6x+6\sqrt{2}-k)=0\end{align}
これが重解 \((x=0)\) を持つので\(,\)
\begin{align}x=\frac{k-6\sqrt{2}}{6}=0\end{align}
\begin{align}k=6\sqrt{2}~~~~\cdots \fbox{答}\end{align}
このとき\(,\) ☆に代入して\(,\)
\begin{align}288t^2-144\sqrt{2}=0\end{align}
\begin{align}t(2t-\sqrt{2})=0\end{align}
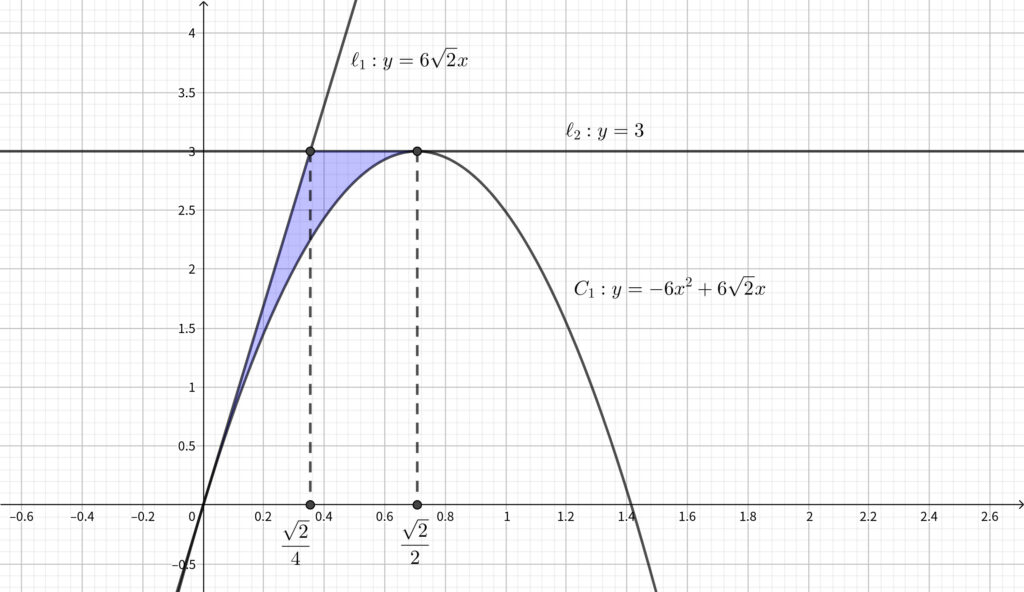
\(t=0\) のとき\(,\) \({\ell}_2~:~y=3\) であるから\(,\) 下図の青色部分を \(x\) 軸に関して回転させたときにできる立体の体積を求めればよい.
求める体積を \(V\) とおくと\(,\)
\begin{align}V=\pi \int_0^{\frac{\sqrt{2}}{4}}\{(6\sqrt{2}x)^2-(-6x^2+6\sqrt{2}x)^2\}dx+\pi \int_{\frac{\sqrt{2}}{4}}^{\frac{\sqrt{2}}{2}}\{3^2-(-6x^2+6\sqrt{2}x)^2\}dx\end{align}
\begin{align}\frac{V}{\pi}=\int_0^{\frac{\sqrt{2}}{4}}(-36x^4+72\sqrt{2}x^3)dx+\int_{\frac{\sqrt{2}}{4}}^{\frac{\sqrt{2}}{2}}(-36x^4+72\sqrt{2}x^3-72x^2+9)dx\end{align}
\begin{align}=\int_0^{\frac{\sqrt{2}}{2}}(-36x^4+72\sqrt{2}x^3)dx+\int_{\frac{\sqrt{2}}{4}}^{\frac{\sqrt{2}}{2}}(-72x^2+9)dx\end{align}
\begin{align}=\biggl[-\frac{36}{5}x^5+18\sqrt{2}x^4\biggr]_0^{\frac{\sqrt{2}}{2}}+\biggl[-24x^3+9x\biggr]_{\frac{\sqrt{2}}{4}}^{\frac{\sqrt{2}}{2}}\end{align}
\begin{align}=-\frac{9\sqrt{2}}{10}+\frac{9\sqrt{2}}{2}-6\sqrt{2}+\frac{9\sqrt{2}}{2}+\frac{3\sqrt{2}}{4}-\frac{9\sqrt{2}}{4}=\frac{3}{5}\sqrt{2}\end{align}
\begin{align}V=\frac{3}{5}\sqrt{2}\pi~~~~\cdots \fbox{答}\end{align}
サ:6 シ:2 ス:3 セ:5 ソ:2







コメント