| 理科大の微積分

東京理科大学理学部（数・物・化）2002年第１問(3)

理（数・物・化）

2022.08.20

理学部（数・物・化）2002年第１問(3)の問題文全文
変曲点であるための必要十分条件
解答〜$f^{\prime\prime}(x)$ の符号の変化も確認〜
補足：グラフの概形

理学部（数・物・化）2002年第１問(3)の問題文全文

関数 $\displaystyle e^{-\frac{1}{x^2}}$ の $x>0$ における変曲点の $x$ 座標は $\displaystyle \frac{~\sqrt{~\fbox{$\hskip0.4emソ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~}{\fbox{$\hskip0.4emタ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}$ である.

変曲点であるための必要十分条件

微分可能な関数 $f(x)$ が第 $2$ 次導関数をもつとします.

このとき$,$ 曲線 $y=f(x)$ の凹凸が変わる境目の点を変曲点といいます.

点 $(a,~f(a))$ が曲線 $y=f(x)$ の変曲点であるための必要十分条件は$,$ 以下の $2$ つを満たすこと.

① 　$f^{\prime\prime}(a)=0$

② 　$x=a$ のまわりで $f^{\prime\prime}(x)$ の符号が変化する

① を満たすだけでは変曲点になるかはわかりません. ② も満たしているかを必ず確認しましょう.

今回の問題はチェックしなくても一意に決まってしまいますが$,$ 問題によっては複数変曲点の候補が出て$,$ そのうちの一部だけが変曲点ということもあり得るので$,$ 必ず確認をします.

解答〜$f^{\prime\prime}(x)$ の符号の変化も確認〜

\begin{align}f(x)=e^{-\frac{1}{x^2}}~~(x>0)\end{align}

とおくと$,$

\begin{align}f^{\prime}(x)=\frac{2}{x^3}e^{-\frac{1}{x^2}}\end{align}

\begin{align}f^{\prime\prime}(x)=-\frac{6}{x^4}e^{-\frac{1}{x^2}}+\frac{2}{x^3}\cdot \frac{2}{x^3}e^{-\frac{1}{x^2}}\end{align}

\begin{align}=\frac{2}{x^6}e^{-\frac{1}{x^2}}(2-3x^2)\end{align}

$x>0$ のとき$,$ $\displaystyle \frac{2}{x^6}e^{-\frac{1}{x^2}}>0$ であるから$,$ $f^{\prime\prime}(x)$ の符号と $2-3x^2$ の符号は一致する.

$x>0$ より$,$ $\displaystyle x=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}$ の前後で符号が正から負に変化する. したがって$,$ 変曲点の $x$ 座標は

\begin{align}x=\frac{\sqrt{6}}{3}~~~~\cdots \fbox{答}\end{align}

ソ：６　タ：３

補足：グラフの概形

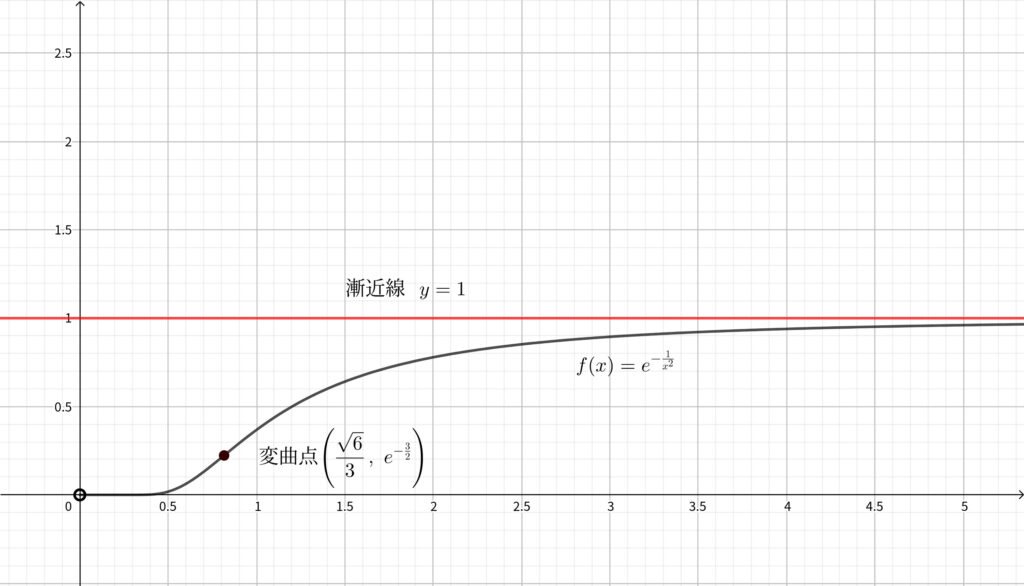
せっかく第 $2$ 次導関数まで求めているので$,$ 増減表を作成してグラフを描いておきます.

\begin{align}\begin{array}{|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle \frac{\sqrt{6}}{3} & \cdots \\ \hline f^{\prime}(x) & {} & + & + & + \\ \hline f^{\prime\prime}(x) & {} & + & 0 & – \\ \hline f(x) & {} & \nearrow \cup & \displaystyle e^{-\frac{3}{2}} & \nearrow \cap \\ \hline \end{array}\end{align}

また$,$

\begin{align}\lim_{x\to +0}e^{-\frac{1}{x^2}}=0,~\lim_{x\to \infty}e^{-\frac{1}{x^2}}=1\end{align}

であるから$,$ $\displaystyle f(x)=e^{-\frac{1}{x^2}}$ のグラフは以下のようになる.