今回は2020年理工学部第3問を解説します. 小問が5つあり, かなり丁寧に誘導がされているため, 誘導にしっかり乗って計算をすれば完答できるかと思います.
問題文全文
定数 \(k (k>0)\) に対し, 関数 \(f(x)\) を定積分
により定義する. ただし, \(e\) は自然対数の底とする.
(1) \(x<1\) のとき, 上の定積分を計算し, \(f(x)\) を \(x\) と \(k\) を用いて表せ.
(2) \(1\leqq x \leqq e^k\) のとき, 上の定積分を計算し, \(f(x)\) を \(x\) と \(k\) を用いて表せ.
(3) 区間 \(1\leqq x\leqq e^k\) における \(f(x)\) の最小値を \(k\) を用いて表せ.
(4) (3) で求めた最小値が 1 となる \(k\) の値を求めよ.
(5) \(k\) を (4) で求めた値とする. このとき, 座標平面において曲線 \(y=f(x)\), \(x\) 軸, 直線\(x=1\), および, 直線 \(x=e^k\) で囲まれた部分の面積を求めよ.
着眼点
基本的には誘導に乗って解答していくだけです。(5) を解く際にグラフの概形を考えますが, (4) で最小値が 1 と言っているので \(y=f(x)\) のグラフは \(x\) 軸よりも上にあることが分かります. それさえ分かれば問題なく面積は求められると思います.
解答
(1) \(x<1\) より, \(0 \leqq t\leqq k\) において, \(e^t>x\) なので,
(2)
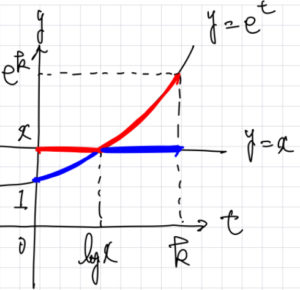
\(y=e^t\) と\(y=x\) の交点の \(t\) 座標は, \(e^t=x\) より, \(t=\log x\) である. 上図より, \(0\leqq t\leqq \log x\) において \(e^t\leqq x\), \(\log x\leqq t\leqq k\) において \(e^t\geqq x\) なので,
(3) \(1\leqq x\leqq e^k\) において, \(f(x)\) は微分可能であるから,
\(f^{\prime}(x)=0\) のとき, \(\displaystyle \log x=\frac{k}{2}\) より, \(\displaystyle x=e^{\frac{k}{2}}\).
増減表は以下のようになる.
\begin{array}{c|c|c|c|c|c}x & 1 & \cdots & \displaystyle e^{\frac{k}{2}} & \cdots & e^k \\ \hline f^{\prime}(x) & {} & – & 0 & + & {}\\ \hline f(x) & {} & \searrow & 最小 & \nearrow & {}\\ \end{array}
よって, 最小値は
(4) (3)より, \(\displaystyle e^k-2e^{\frac{k}{2}}+1=1\) のとき,
\(\displaystyle e^{\frac{k}{2}}>0\) より, \(\displaystyle e^{\frac{k}{2}}=2\) つまり, \(k=2\log 2\).
(5) (4)の増減表により, \(y=f(x)\) のグラフは下図のようになる. 求める面積を \(S\) とおくと,
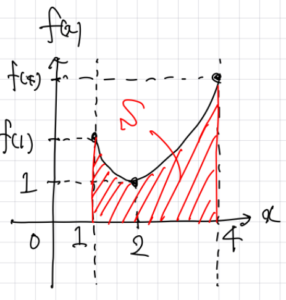
補足説明(端点の大小関係)
(5) 図では, \(f(1)\) よりも \(f(4)\) の方が大きいように描いている. 問題を解くだけなら不要であるが, その根拠を下に記しておく.
\(f(x)=x\left(2\log x -2\log 2 -2\right)+5\) より,
ここで,
より, \(\displaystyle \frac{e^3}{4}<\frac{256}{e^3}\) であり, 底 \(e>1\) だから, \(f(1)<f(4)\).



