東京理科大学C方式・グローバル方式2022年第６問| 理科大の微積分

C方式・グローバル方式2022年第６問の問題文全文
事前の準備〜何度も使うものは予め準備〜
(1) の解答〜準備してあるから代入だけでOK〜
(2) の解答〜（多項式）× $e^{-x}$ 型の積分〜
(3) の解答

C方式・グローバル方式2022年第６問の問題文全文

$a$ を正の実数とする. $x$ が実数全体を動くとき$,$ 関数 $f(x)=(1-ax)e^{-x}$ は $x=\beta $ で最小値をとるとする. 以下の問いに答えよ. ただし$,$ $e$ は自然対数の底を表す.

(1) $a=3$ のとき$,$ $\displaystyle \beta =\frac{~\fbox{$\hskip0.4emお\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emか\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}$ であり$,$ 最小値 $f(\beta )$ は $\displaystyle -~\fbox{$\hskip0.4emき\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~e^{^{-~\frac{~\fbox{$\hskip0.4emく\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emけ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}}}$ である.

(2) $a=2$ のとき$,$ $\displaystyle \beta =~\frac{~\fbox{$\hskip0.4emこ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emさ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}$ であり$,$

\begin{align}\int_{\beta}^{1+\beta}f(x)dx=\left(~\fbox{$\hskip0.4emし\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~e^{^{-~\fbox{$\hskip0.4emす\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}}~-~\fbox{$\hskip0.4emせ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\right)~e^{-\beta}\end{align}

である.

(3) $a=1$ とする. 曲線 $y=f(x)$ の $\beta \leqq x \leqq 1+\beta $ の部分を $C$ とする. $C$ 上の端点ではない点 $(t,~f(t))$ における接線を $\ell $ とする. $2$ 本の直線 $x=\beta $ と $\ell $ および曲線 $C$ で囲まれた図形の面積を $S_1(t)$ とする. また$,$ $2$ 本の直線 $x=1+\beta $ と $\ell $ および曲線 $C$ で囲まれた図形の面積を $S_2(t)$ とする. $t$ が $\beta < t < 1+\beta $ の範囲を動くとき$,$ $2$ つの面積の和 $S_1(t)+S_2(t)$ は $\displaystyle t=~\frac{~\fbox{$\hskip0.4emそ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emた\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}$ で最小値をとる.

事前の準備〜何度も使うものは予め準備〜

\begin{align}f^{\prime}(x)=-ae^{-x}+(1-ax)(-e^{-x})=(ax-a-1)e^{-x}\end{align}

$e^{-x}>0$ より$,$ $f^{\prime}(x)$ の符号は $ax-a-1$ の符号と一致するから$,$ $a>0$ のときの増減表は以下のようになる.

\begin{align}\begin{array}{|c|c|c|c|}\hline x & \cdots & \displaystyle \frac{a+1}{a} & \cdots \\ \hline f^{\prime}(x) & – & 0 & + \\ \hline f(x) & \searrow & 極小 & \nearrow \\ \hline \end{array}\end{align}

quandle

(1)(2)(3)のそれぞれで増減表が必要になりそうなので最初に作っておきましょう！

また$,$$a>0$ のときと $a<0$ のときは $f^{\prime}(x)$ の符号が変わりますが$,$ 今回は $a=1,~2,~3$ のときを計算することになるので $a>0$ のときに絞っておいてOKです！

増減表より$,$ $\displaystyle \beta =\frac{a+1}{a}$ である.

(1) の解答〜準備してあるから代入だけでOK〜

$a=3$ のとき$,$

\begin{align}\beta =\frac{3+1}{3}=\frac{4}{3}~~~~\cdots \fbox{答}\end{align}

最小値 $f(\beta )$ は$,$

\begin{align}f\left(\frac{4}{3}\right)=\left(1-3\cdot \frac{4}{3}\right)e^{-\frac{4}{3}}=-3e^{-\frac{4}{3}}~~~~\cdots \fbox{答}\end{align}

お：４か：３き：３く：４け：３

(2) の解答〜（多項式）× $e^{-x}$ 型の積分〜

$a=2$ のとき$,$

\begin{align}\beta =\frac{2+1}{2}=\frac{3}{2}~~~~\cdots \fbox{答}\end{align}

\begin{align}\int_{\beta}^{1+\beta }(1-2x)e^{-x}dx=\biggl[-(1-2x-2)e^{-x}\biggr]_{\beta}^{1+\beta}\end{align}

\begin{align}=\biggl[(2x+1)e^{-x}\biggr]_{\beta}^{1+\beta}=(2\beta +3)e^{-1-\beta}-(2\beta+1)e^{-\beta}\end{align}

\begin{align}=(6e^{-1}-4)e^{-\beta}~~~~\cdots \fbox{答}\end{align}

quandle

部分積分を繰り返すことで$,$

\begin{align} \int f(x)e^{-x}dx=-(f(x)+f^{\prime}(x)+f^{\prime \prime}(x)+\cdots )e^{-x}+C\end{align}

となります. 特に $f(x)$ が多項式の場合は微分を繰り返すことで $0$ になりますから$,$ 一発で不定積分が求められる便利公式です.

こ：３さ：２し：６す：１せ：４

(3) の解答

グラフの概形をかき$,$ 面積を求める図形を把握する

$a=1$ のとき$,$

\begin{align}\beta =2,~f(\beta )=-e^{-2}\end{align}

また$,$ 極限値は

\begin{align}\lim_{x\to -\infty}f(x)=\infty ,~\lim_{x\to \infty}f(x)=0\end{align}

であり$,$ $f^{\prime}(x)=(x-2)e^{-x}$ より$,$ 接線 $\ell $ は

\begin{align}\ell ~:~y=(t-2)e^{-t}(x-t)+(1-t)e^{-t}\end{align}

\begin{align}\ell ~:~y=(t-2)e^{-t}x+(-t^2+t+1)e^{-t}\end{align}

であるから$,$ 面積を求めたい図形は下図の赤色部分.

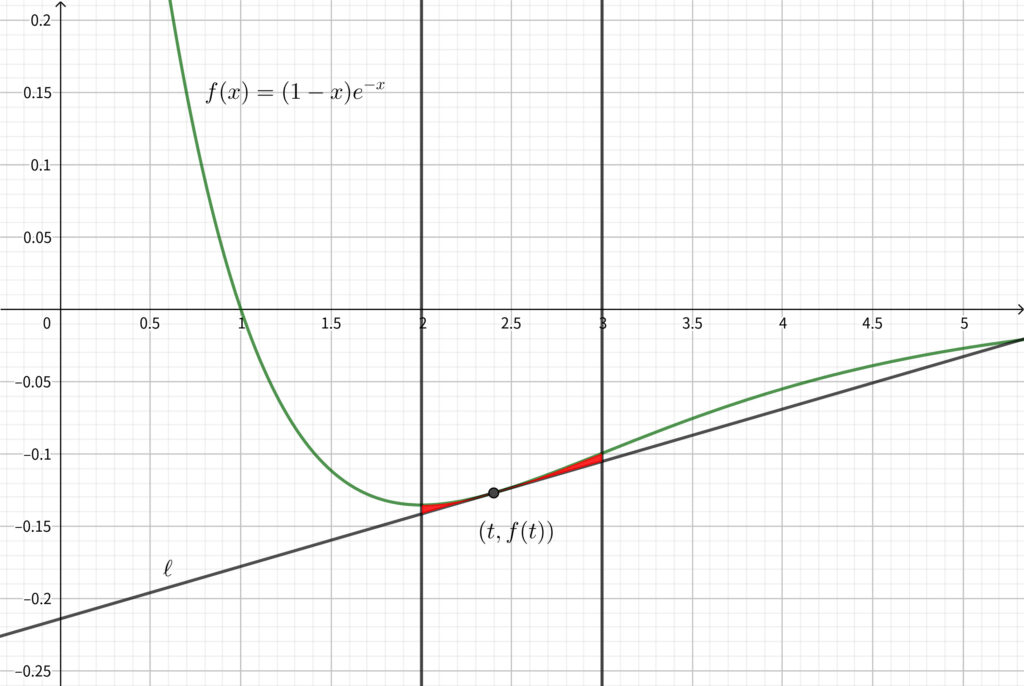
赤色部分の面積は下図のオレンジ部分の面積から青色部分の面積を引いたものと一致する.

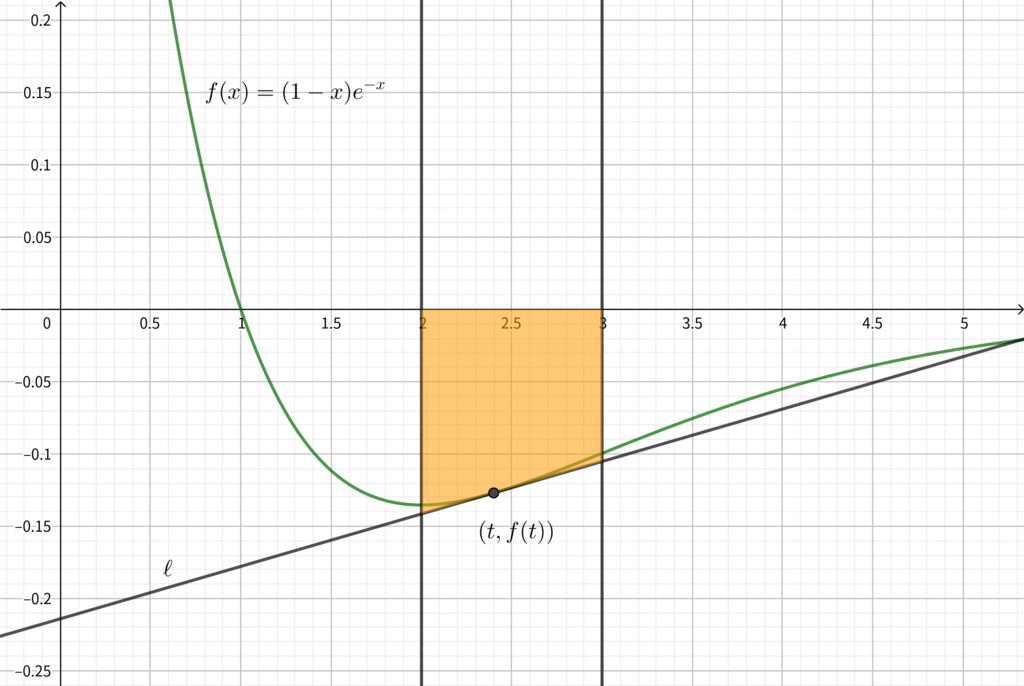
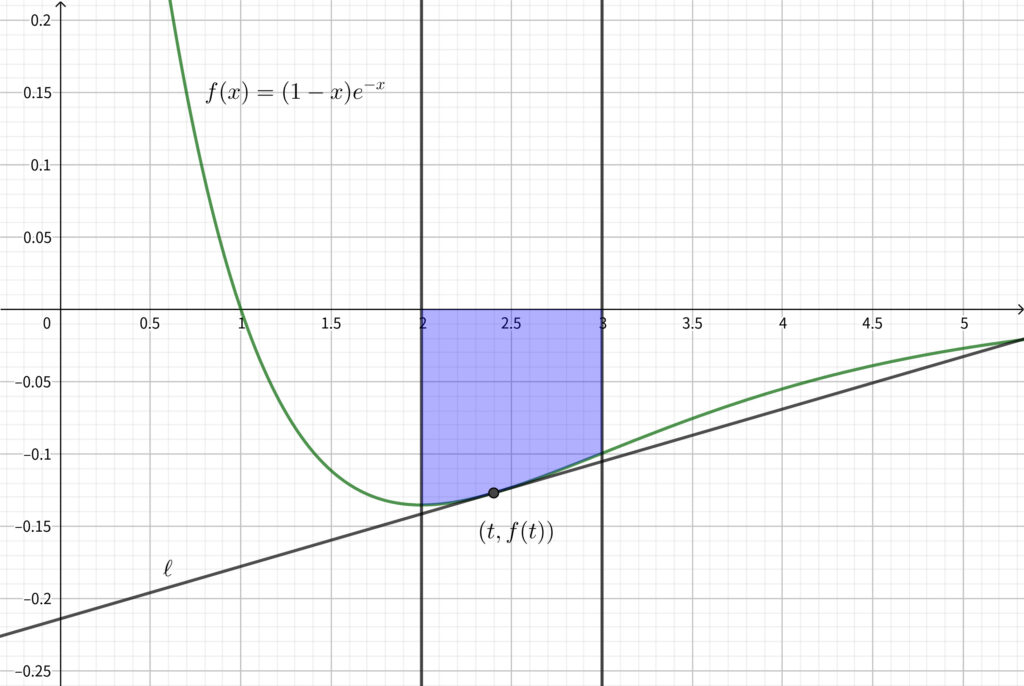
青色部分の面積は定数であるから$,$ $C$ とおく.

$x=2$ のとき$,$ $y=(-t^2+3t-3)e^{-t}$

$x=3$ のとき$,$ $y=(-t^2+4t-5)e^{-t}$

であるから$,$ 求める面積を $S(t)$ とおくと$,$

\begin{align}S(t)=S_1(t)+S_2(t)\end{align}

\begin{align}=\frac{1}{2}\{(t^2-3t+3)e^{-t}+(t^2-4t+5)e^{-t}\}\cdot 1-C\end{align}

\begin{align}=\frac{2t^2-7t+8}{2}e^{-t}-C\end{align}

\begin{align}S^{\prime}(t)=\frac{4t-7}{2}e^{-t}-\frac{2t^2-7t+8}{2}e^{-t}\end{align}

\begin{align}=\frac{-2t^2+11t-15}{2}e^{-t}=\frac{-(t-3)(2t-5)}{2}e^{-t}\end{align}

$2<t<3$ において$,$ $\displaystyle -\frac{t-3}{2}e^{-t}>0$ であるから$,$ $S^{\prime}(t)$ の符号は$,$ $2t-5$ の符号と一致する. よって$,$ 増減表は以下のようになる.

\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline t & 2 & \cdots & \displaystyle \frac{5}{2} & \cdots & 3 \\ \hline S^{\prime}(t) & {} & – & 0 & + & 0 \\ \hline S(t) & {} & \searrow & 極小 & \nearrow & {} \\ \hline \end{array}\end{align}

増減表より $\displaystyle t=\frac{5}{2}$ のとき最小値をとる.

そ：５た：２

おまけ：$C$ の実際の値

$C$ は定数なので求める必要はありませんが$,$ 求めてみます.

\begin{align}C=\int_2^3(x-1)e^{-x}dx\end{align}

\begin{align}=\biggl[-(x-1-1)e^{-x}\biggr]_2^3=\biggl[(2-x)e^{-x}\biggr]_2^3=e^{-3}~~~~\cdots \fbox{答}\end{align}

おまけ：最小値の実際の値

最小値も求める必要はありませんが$,$ 求めてみます.

\begin{align}S\left(\frac{5}{2}\right)=\left(\frac{25}{4}-\frac{7}{2}\cdot \frac{5}{2}+4\right)e^{-\frac{5}{2}}-e^{-3}=\frac{3}{2}e^{-\frac{5}{2}}-e^{-3}~~~~\cdots \fbox{答}\end{align}