経営学部（ビジネスエコノミクス学科のみ）2020年第４問

問題文全文

座標空間に

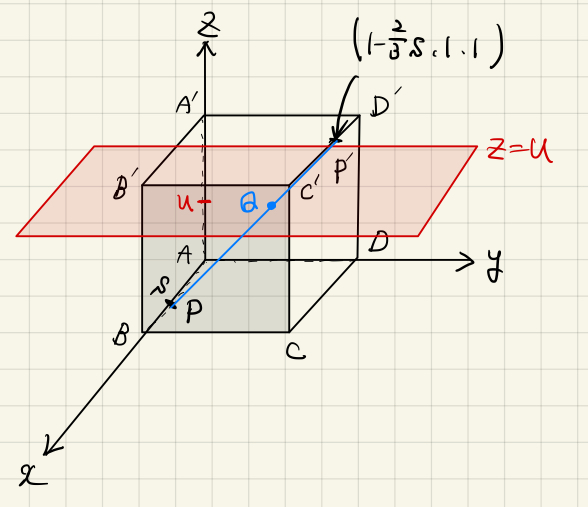
を頂点とする 1 辺の長さが 1 の立方体がある. \(s\) を \(0\leqq s\leqq 1\) を満たす実数とするとき\(,\) 辺 \(\mathrm{AB}\) 上に \((s,~0,~0)\) を座標とする点 \(\mathrm{P}\) をとる. また\(,\) 辺 \(\mathrm{D^{\prime}C^{\prime}}\) 上に \(\displaystyle \left(1-\frac{2}{3}s,~1,~1\right)\) を座標とする点 \(\mathrm{P}^{\prime}\) をとる. このとき次の問いに答えなさい.

(1) \(u\) を \(0\leqq u\leqq 1\) を満たす実数とするとき\(,\) 平面 \(z=u\) と線分 \(\mathrm{PP^{\prime}}\) の交点 \(\mathrm{Q}\) の座標を求めなさい.

(2) 線分 \(\mathrm{PP^{\prime}}\) を \(z\) 軸のまわりに回転させた時にできる図形と 2 つの平面 \(z=0,~z=1\) で囲まれる立体の体積 \(V\) を \(s\) を用いて表しなさい.

(3) 点 \(\mathrm{P}\) が辺 \(\mathrm{AB}\) を動くとき\(,~V\) が最小になるときの \(s\) の値を求めなさい.

(1) の着眼点

もしかしたら何をやればいいのかわからないという人がいるかもしれません. 座標平面で 2 つのグラフの交点の座標を求めることはできるのではないでしょうか.

空間になるとよくわからないという人がいますが\(,\) やるべきことは一緒です. 線分 \(\mathrm{PP^{\prime}}\) の方程式を求めて\(,\) \(z=u\) と連立をすればいいのです.

空間の直線の方程式はベクトル方程式で表すことができます.

(1) の解答

直線 \(\mathrm{PP^{\prime}}\) 上の任意の点 \(\mathrm{R}\) に対して\(,\)

平面 \(z=u\) と線分 \(\mathrm{PP^{\prime}}\) との交点 \(\mathrm{Q}\) の位置ベクトルは\(,\) \(z=u\) のときの点 \(\mathrm{R}\) に一致するから\(,\)

(2) の着眼点

空間上の直線を \(z\) 軸に関して 1 回転させたときにできる立体の体積を求める問題です.

・直線が \(z\) 軸に平行なら回転体は円柱です.

・直線が \(z\) 軸と交点を持つなら回転体は円錐面になります. （ \(z\) 軸に垂直な場合を除く）

・今回の問題のように\(,\) 直線と \(z\) 軸がねじれの位置にあるときは\(,\) 回転一様双曲面というものになります.

回転体の体積を考えるときはある平面で切ったときの断面積を求めて積分することを考えます.

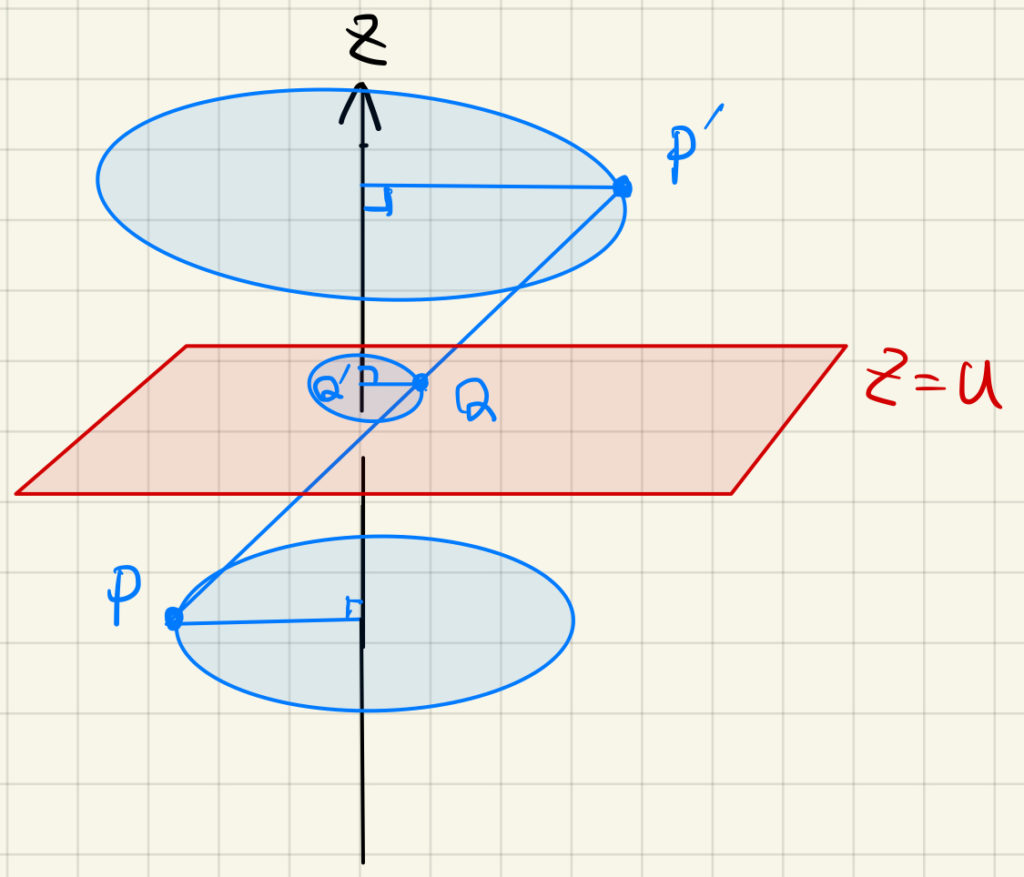
直線を平面で切ると１点が現れます. この１点を \(z\) 軸に関して回転させた円が断面になります. この円の半径は１点から \(z\) 軸に下ろした垂線の足までの距離に一致します.

今回の問題でいえば平面 \(z=u\) と直線 \(\mathrm{PP^{\prime}}\) の交点 \(\mathrm{Q}\) から \(z\) 軸に下ろした垂線の足を \(\mathrm{Q^{\prime}}(0,~0,~u)\) とするとき\(,\) \(\mathrm{QQ^{\prime}}\) が半径です.

(2) の解答

\(\mathrm{Q^{\prime}}(0,~0,~u)\) とおくと

よって\(,\)

(3) の解答

\(f(s)\) が最小となるとき\(,\) \(V\) も最小をとる.

\(0≤s≤1\) より\(,\) \(\displaystyle s=\frac{3}{14}\).