理学部第二部（数学科専用）2021年第４問

問題文全文

\(\displaystyle f(x)=\frac{\sin{x}}{x}~\left(\frac{\pi}{2}<x<\frac{3\pi}{2}\right)\) とおく. 以下の問いに答えよ.

(1) 関数 \(y=f(x)\) が \(x=a\) で極値をとるならば\(,\) \(a=\tan{a}\) を満たすことを示せ.

(2) \(\displaystyle g(x)=x-\tan{x}~\left(\frac{\pi}{2}<x<\frac{3\pi}{2}\right)\) とおく.

　(a) 関数 \(y=f(x)\) はつねに減少することを示せ. また\(,\) \(g(b)=0\) をみたす実数 \(b\) がただ \(1\) つあり\(,\) \(\displaystyle \pi <b<\frac{3\pi}{2}\) をみたすことを示せ.

　(b) \(f(x)\) は \(x=b\) で極小値をとることを示せ. ただし\(,\) \(b\) は (a) で求めたものとする.

　(c) \(\displaystyle f(b)=-\frac{1}{\sqrt{b^2+1}}\) を示せ. ただし\(,\) \(b\) は (a) で求めたものとする.

(1) の解答

\(x=a\) で極値をとるので\(,\) \(f^{\prime}(a)=0\)

\(\displaystyle \frac{\pi}{2}<a<\frac{3\pi}{2}\) より\(,\) \(\cos{a}\neq 0\) であるから\(,\)

quandle

「極値をとる」という問題文はかなり慎重になりましょう.

\begin{align}x=a~で極値をとる \Rightarrow f^{\prime}(a)=0\end{align}

は真ですが\(,\) その逆は一般に成り立たないからです.

今回は逆の検証は必要ありませんが\(,\) 問題文が

「極大値をとる」「極小値をとる」

の場合は逆の検証が必要です. 極値をとるのは確かでも本当に極大値や極小値をとるかはわからないからです.

(2) (a) の着眼点

①　「減少する」ことを示したいので\(,\) \(g^{\prime}(x)\leqq 0\) を示しましょう.

②　「\(g(b)=0\) となる実数 \(b\) がただ一つ存在する」ことを示すには中間値の定理を利用します.

今回は①で単調減少であることを示しているので残り示さないといけないことは

１、\(g(x)\) が連続関数であること

２、\(\displaystyle g(\pi)>0 かつ \lim_{x\to \frac{3\pi}{2}-0}g(x)<0\)

です. \(g(x)\) が \(\displaystyle x=\frac{3\pi}{2}\) で定義できないので極限値を調べます.

(2) (a) の解答

よって\(,\) \(g(x)\) はつねに減少する.

quandle

三角関数の相互関係より

\begin{align}1+\tan^2{x}=\frac{1}{\cos^2{x}}\end{align}

ですね. これを変形して\(,\)

\begin{align}1-\frac{1}{\cos^2{x}}=-\tan^2{x}\end{align}

になります.

また\(,\) \(g(x)\) は単調減少な連続関数であり\(,\)

であるから\(,\) 中間値の定理により\(,\) \(g(b)=0\) となる実数 \(b\) が\(,\) ただ一つ存在し\(,\) \(\displaystyle \pi <b<\frac{3\pi}{2}\) をみたす.

(2) (b) の着眼点

とかけます.

ですから\(,\) \(g(x)\) の符号を調べることで \(f^{\prime}(x)\) の符号を調べられそうです.

\(g(x)\) の符号が \(b\) の前後でどうなるかを (a) で調べたことから判断しましょう.

(2) (b) の解答

ここで\(,\) (a) で求めた \(b\) を持ってくると\(,\) \(g(b)=0\) であることから\(,\) \(f^{\prime}(b)=0\)

\(\displaystyle \pi <x<\frac{3\pi}{2}\) において \(x^2\cos{x}<0\) であるから\(,\) \(f^{\prime}(x)\) の符号は \(g(x)\) の符号の逆になる. このことに注意して増減表をかくと以下のようになる.

増減表より\(,\) \(f(x)\) は \(x=b\) で極小値をとる.

(2) (c) の解答

\(g(b)=0\) より\(,\)

\(\displaystyle 1+\tan^2{b}=\frac{1}{\cos^2{b}}\) より\(,\)

\(\sin^2{b}=1-\cos^2{b}\) より\(,\)

\(\displaystyle \pi < b < \frac{3\pi}{2}\) より\(,\) \(\sin{b}<0\) であるから\(,\)

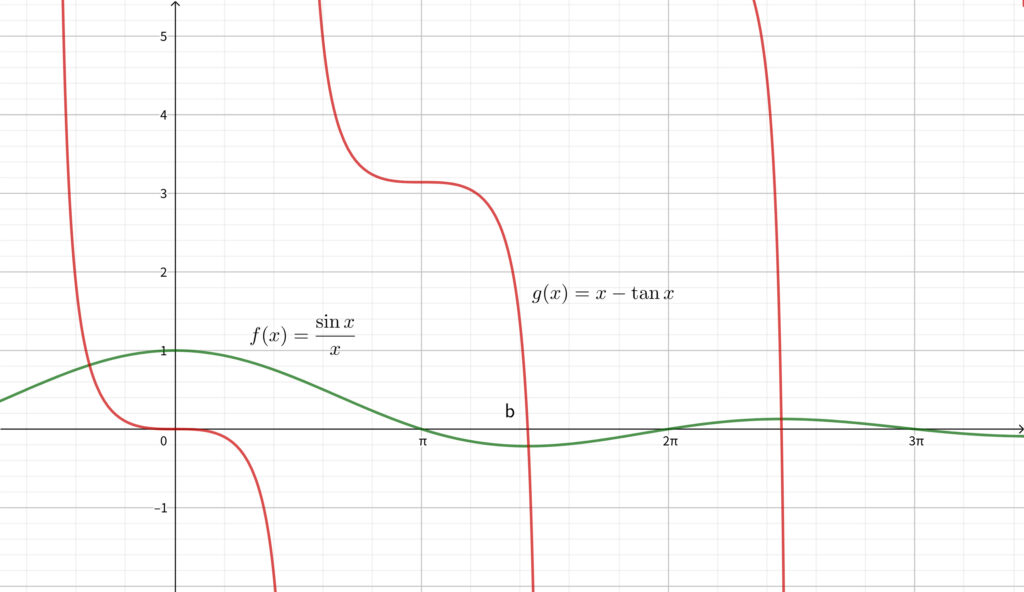
※なお\(,\) \(y=f(x)\) と \(y=g(x)\) のグラフは以下のようになります.