問題文全文
\(x\) を \(2\) より小さい実数として\(,\) 関数 \(f(x)\) を
\begin{align}f(x)=\frac{4x-7}{x-2}~~(x<2)\end{align}
と定め\(,\) 座標平面上で曲線 \(y=f(x)\) を考える.
(1) 曲線 \(y=f(x)\) のグラフの概形を座標平面上に描け.
(2) 点 \(\displaystyle \left(\frac{5}{4},~f\left(\frac{5}{4}\right)\right)\) における曲線 \(y=f(x)\) の接線の方程式を求めよ.
(3) 直線 \(5x-2y=a\) が曲線 \(y=f(x)\) の法線となるときの実数 \(a\) の値を求めよ.
(4) 曲線 \(y=f(x)\) と \(x\) 軸\(,\) \(y\) 軸で囲まれた図形の面積 \(S\) を求めよ.
(5) 曲線 \(y=f(x)\) と \(x\) 軸\(,\) \(y\) 軸で囲まれた図形を \(x\) 軸のまわりに \(1\) 回転してできる回転体の体積 \(V\) を求めよ.
(1) の解答
\begin{align}f(x)=\frac{4(x-2)+1}{x-2}=4+\frac{1}{x-2}\end{align}
これは\(,\) \(\displaystyle y=\frac{1}{x}\) のグラフを \(x\) 軸方向に \(2,\) \(y\) 軸方向に \(4\) だけ平行移動したグラフになるので\(,\) 概形は以下のようになる.
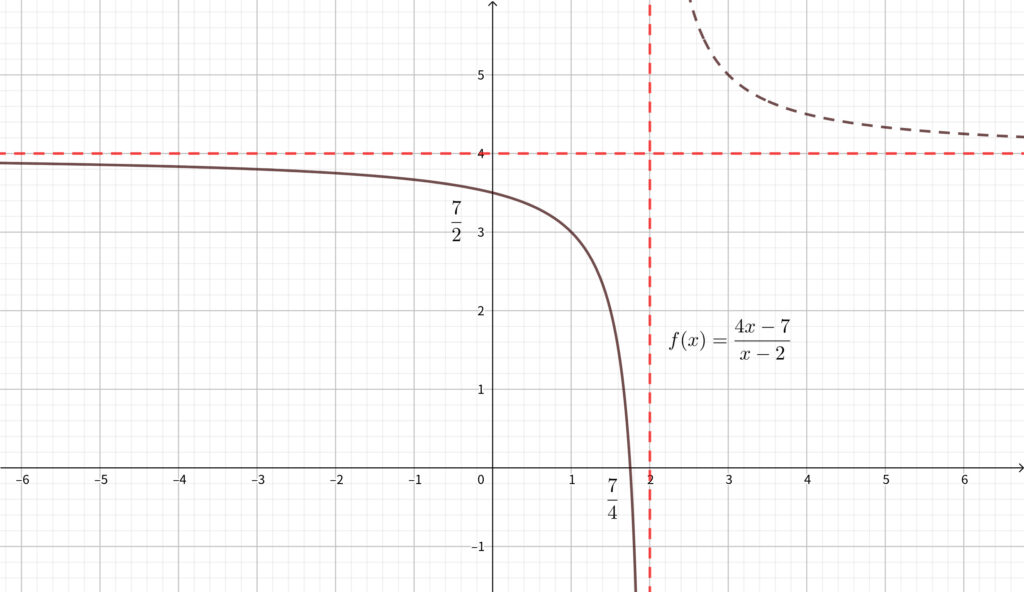
(2) の解答
\begin{align}f^{\prime}(x)=-\frac{1}{(x-2)^2}\end{align}
より\(,\)
\begin{align}f^{\prime}\left(\frac{5}{4}\right)=-\frac{16}{9}\end{align}
であるから\(,\) \(\displaystyle \left(\frac{5}{4},~\frac{8}{3}\right)\) における接線は\(,\)
\begin{align}y=-\frac{16}{9}\left(x-\frac{5}{4}\right)+\frac{8}{3}\end{align}
\begin{align}y=-\frac{16}{9}x+\frac{44}{9}~~~~\cdots \fbox{答}\end{align}
(3) の解答
\begin{align}5x-2y=a~\Leftrightarrow ~y=\frac{5}{2}x-\frac{a}{2}\end{align}
より\(,\) 法線の傾きが \(\displaystyle \frac{5}{2}\) であるから\(,\)
\begin{align}-\frac{1}{f^{\prime}(x)}=(x-2)^2=\frac{5}{2}\end{align}
\(x<2\) に注意して\(,\)
\begin{align}x=2-\frac{\sqrt{10}}{2}\end{align}
このとき\(,\) 接点の \(y\) 座標は
\begin{align}f\left(2-\frac{\sqrt{10}}{2}\right)=4+\cfrac{1}{\left(2-\cfrac{\sqrt{10}}{2}\right)-2}\end{align}
\begin{align}=4-\frac{2}{\sqrt{10}}=4-\frac{\sqrt{10}}{5}\end{align}
となる. 接点 \(\displaystyle \left(2-\frac{\sqrt{10}}{2},~4-\frac{\sqrt{10}}{5}\right)\) における法線は
\begin{align}y=\frac{5}{2}\left\{x-\left(2-\frac{\sqrt{10}}{2}\right)\right\}+4-\frac{\sqrt{10}}{5}\end{align}
\begin{align}y=\frac{5}{2}x-5+\frac{5\sqrt{10}}{4}+4-\frac{\sqrt{10}}{5}\end{align}
\begin{align}y=\frac{5}{2}x+\frac{21\sqrt{10}}{20}-1\end{align}
法線の \(y\) 切片は \(\displaystyle -\frac{a}{2}\) であるから\(,\)
\begin{align}-\frac{a}{2}=\frac{21\sqrt{10}}{20}-1\end{align}
\begin{align}a=2-\frac{21\sqrt{10}}{10}~~~~\cdots \fbox{答}\end{align}
(4) の解答
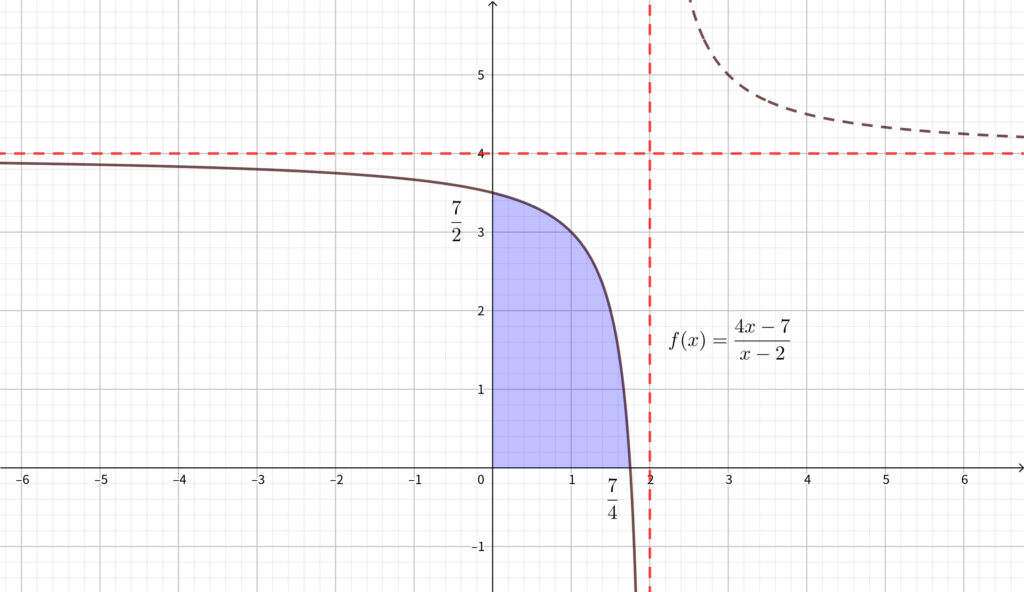
上図の青色部分の面積を求めればよい.
\begin{align}S=\int_0^{\frac{7}{4}}\left(4+\frac{1}{x-2}\right)dx\end{align}
\begin{align}=\biggl[4x+\log{|x-2|}\biggr]_0^{\frac{7}{4}}=7+\log{\frac{1}{4}}-\log{2}=7-3\log{2}~~~~\cdots \fbox{答}\end{align}

quandle
上図を見ると\(,\) 青色部分の面積は \(1\times 1\) の正方形 \(7\) 個分より小さくなっていますね. 確かに \(7\) より小さい数で答えが出ています.
(5) の解答
(4) の青色部分を \(x\) 軸のまわりに \(1\) 回転したときの体積を求めればよい.
\begin{align}V=\pi \int_0^{\frac{7}{4}}\left(4+\frac{1}{x-2}\right)^2dx\end{align}
\begin{align}\frac{V}{\pi}=\int_0^{\frac{7}{4}}\left\{16+\frac{8}{x-2}+\frac{1}{(x-2)^2}\right\}dx\end{align}
\begin{align}=\biggl[16x+8\log{|x-2|}-\frac{1}{x-2}\biggr]_0^{\frac{7}{4}}\end{align}
\begin{align}=28+8\log{\frac{1}{4}}+4-8\log{2}-\frac{1}{2}=\frac{63}{2}-24\log{2}\end{align}
\begin{align}V=\left(\frac{63}{2}-24\log{2}\right)\pi~~~~\cdots \fbox{答}\end{align}

quandle
どれも教科書レベルの基本的な問題です. ゆえに特に着眼点はありません. 計算ミスのないように注意し\(,\) 確実に得点したいです.








コメント