経営学部（共通）2022年第３問（１）の問題文全文
関数 \(f(x)\) を \(f(x)=|x^2-4|\) と定める. 座標平面において\(,\) 曲線 \(y=f(x)\) 上の点 \((1,~3)\) における接線の方程式を \(y=g(x)\) とする. 接点 \((1,~3)\) を除く\(,\) 曲線 \(y=f(x)\) と直線 \(y=g(x)\) の \(2\) つの交点の \(x\) 座標を \(\alpha \) と \(\beta\) とする. \(\alpha < \beta \) として\(,\) 次の定積分を求めなさい.
\begin{align}\int_{\alpha}^{\beta}\{g(x)-f(x)\}dx\end{align}
着眼点〜面積として見る〜
\begin{align}\int_{\alpha}^{\beta}\{g(x)-f(x)\}dx\end{align}
という形から面積として見れないかを考えるのが自然です.
そのためにはまずどんな図形になるのかを正確に把握しましょう.
\(y=f(x)\) は全体に絶対値がついた関数なので\(,\) \(x\) 軸よりも下の部分を \(x\) 軸に関して折り返したものになります.
解答
\begin{align}f(x)=|x^2-4|=\left\{\begin{array}{cc}x^2-4 & (x\leqq -2,~2\leqq x) \\ -x^2+4 & (-2<x<2) \\ \end{array}\right. \end{align}
より\(,\) \(-2<x<2\) において\(,\) \(f^{\prime}(x)=-2x\) であるから\(,\) \(f^{\prime}(1)=-2\).
よって\(,\) 点 \((1,~3)\) における接線は
\begin{align}g(x)=-2(x-1)+3=-2x+5\end{align}
ここで\(,\) \(x=\alpha ,~\beta\) は
\begin{align}x^2-4=-2x+5\end{align}
の解であるから\(,\)
\begin{align}x^2+2x-9=0\end{align}
\begin{align}x=-1\pm \sqrt{10}\end{align}
\(\alpha <\beta \) より\(,\)
\begin{align}\alpha =-1-\sqrt{10},~\beta =-1+\sqrt{10}\end{align}
\(y=f(x)\) のグラフと \(y=g(x)\) のグラフの位置関係は以下の図のようになる.
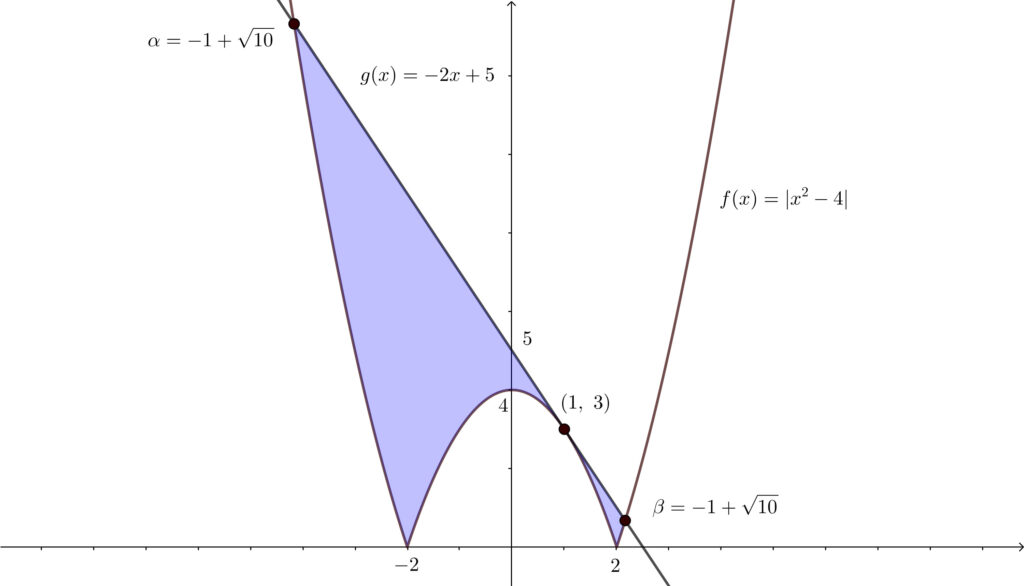
求める定積分の値は上図の面積と一致する.
1/6 パズルで面積を求める
上図の青色部分は下図の赤色部分からオレンジ色部分を抜いた部分と見ることができます.
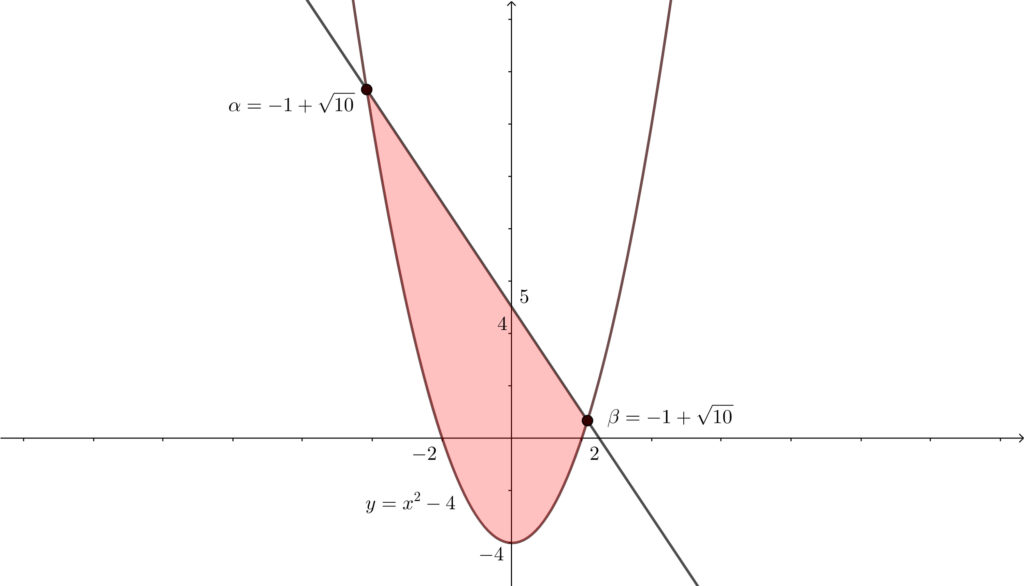\(y=x^2-4\) のグラフと \(y=-2x+5\) のグラフで囲まれる部分
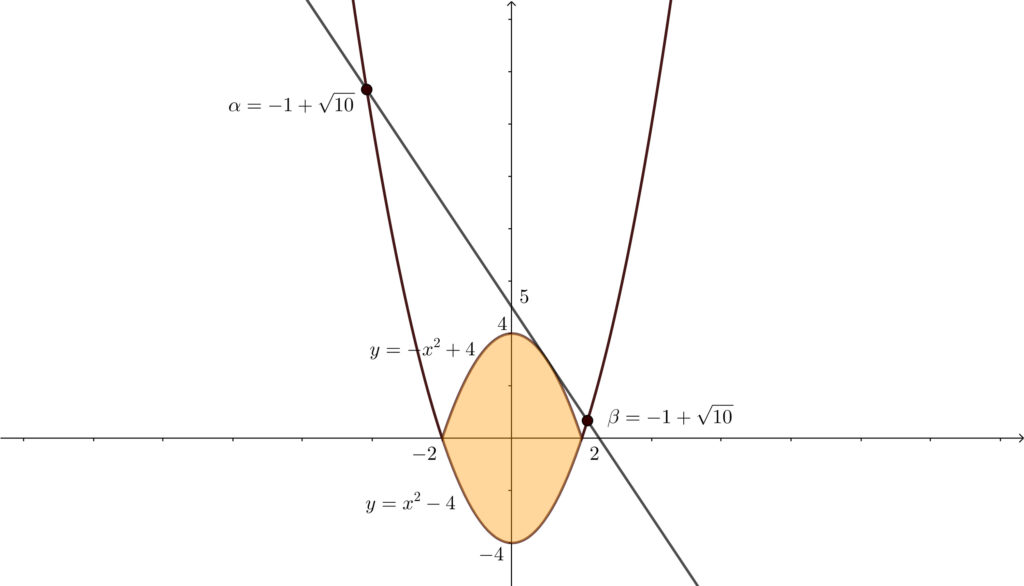\(y=-x^2+4\) のグラフと \(y=x^2-4\) のグラフで囲まれる部分
赤色部分は「放物線と直線で囲まれる部分」ですし\(,\) オレンジ色部分は「 \(2\) つの放物線で囲まれる部分」ですから\(,\) どちらも 「1/6 公式」を用いて求めることができます.
1/6 公式については以下の記事でまとめていますので参考にしてください！
\(\displaystyle \int_{\alpha}^{\beta}\{g(x)-f(x)\}dx\) の計算
\begin{align}\int_{\alpha}^{\beta}\{g(x)-f(x)\}dx=\int_{\alpha}^{\beta}(-2x+5-|x^2-4|)dx\end{align}
\begin{align}=\int_{\alpha}^{\beta}\{-2x-5-(x^2-4)\}dx-\int_{-2}^2\{-x^2+4-(x^2-4)\}dx\end{align}
\begin{align}=\int_{\alpha}^{\beta}-(x- \alpha )(x-\beta )dx-\int_{-2}^2-2(x-2)(x+2)dx\end{align}
\begin{align}=\frac{1}{6}\{-1+\sqrt{10}-(-1-\sqrt{10})\}^3-\frac{2}{6}\{2-(-2)\}^3\end{align}
\begin{align}=\frac{80\sqrt{10}}{6}-\frac{64}{3}=\frac{40\sqrt{10}-64}{3}~~~~\cdots \fbox{答}\end{align}
コメント