奇関数・偶関数の積分公式とは
\begin{align}\int_{-a}^af(x)dx=\left\{\begin{array}{cc} 0 & (~f(x)~:~奇関数~)\\ \displaystyle 2\int_0^af(x)dx & (~f(x)~:~偶関数~)\end{array}\right.\end{align}
積分範囲が \(-a\leqq x \leqq a\) のときは\(,\) ぜひこの公式が使えないかを疑いましょう. \(f(x)\) が奇関数か偶関数のときはどちらも計算量を減らすことができるからです.
\(f(x)\) が奇関数であれば即座に \(0\) とできますし\(,\) 偶関数であっても代入するものが \(-a\) だったものが \(0\) に変わるので\(,\) 計算が楽になるからです.
奇関数・偶関数の定義と性質
関数 \(f(x)\) が
\begin{align}f(-x)=-f(x)\end{align}
を満たすとき\(,\) 奇関数といい\(,\)
\begin{align}f(-x)=f(x)\end{align}
を満たすとき\(,\) 偶関数といいます.
奇関数の例
\begin{align}x^3,~\sin{x},~\tan{x}\end{align}
などは奇関数です.それぞれ以下のようなグラフになります. 共通点は何でしょうか.
 \(y=x^3\) のグラフ
\(y=x^3\) のグラフ
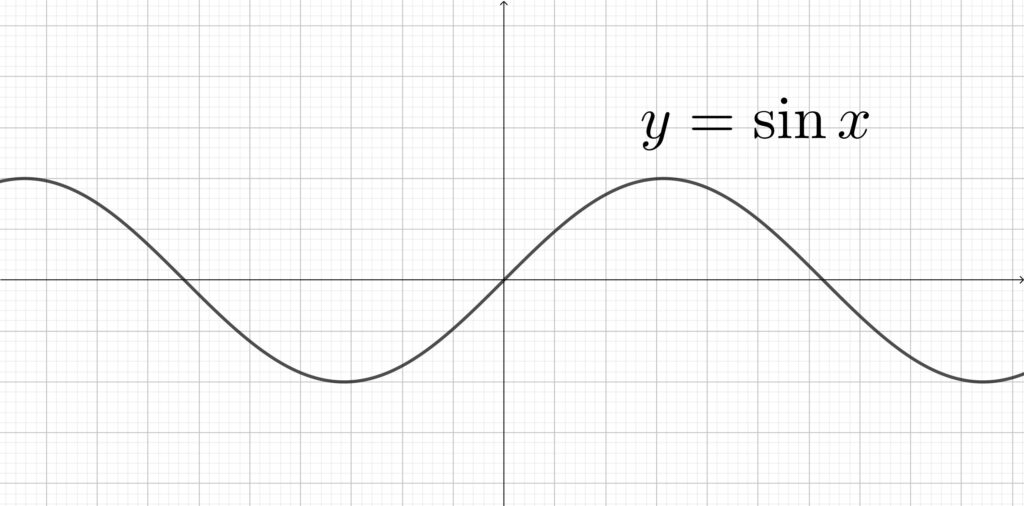 \(y=\sin{x}\) のグラフ
\(y=\sin{x}\) のグラフ
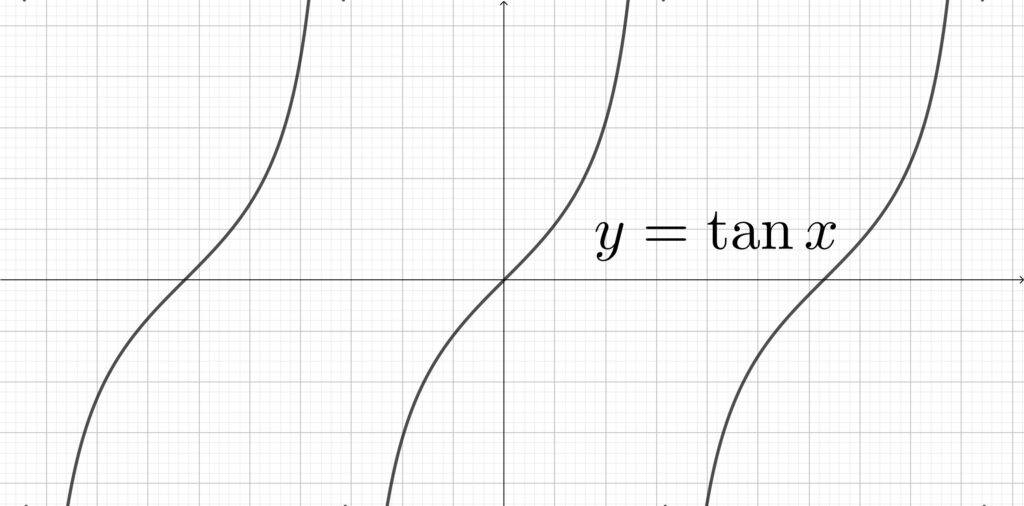 \(y=\tan{x}\) のグラフ
\(y=\tan{x}\) のグラフ
上図からわかるように\(,\) 奇関数のグラフはすべて原点対称になります.
偶関数の例
\begin{align}x^2,~\cos{x},~|x|\end{align}
などは偶関数です. それぞれ以下のようなグラフになります.
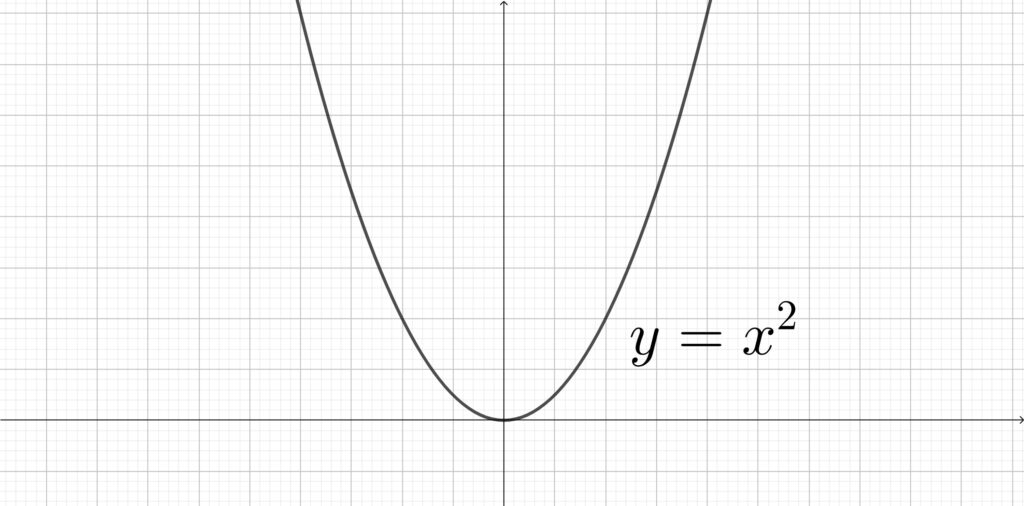 \(y=x^2\) のグラフ
\(y=x^2\) のグラフ
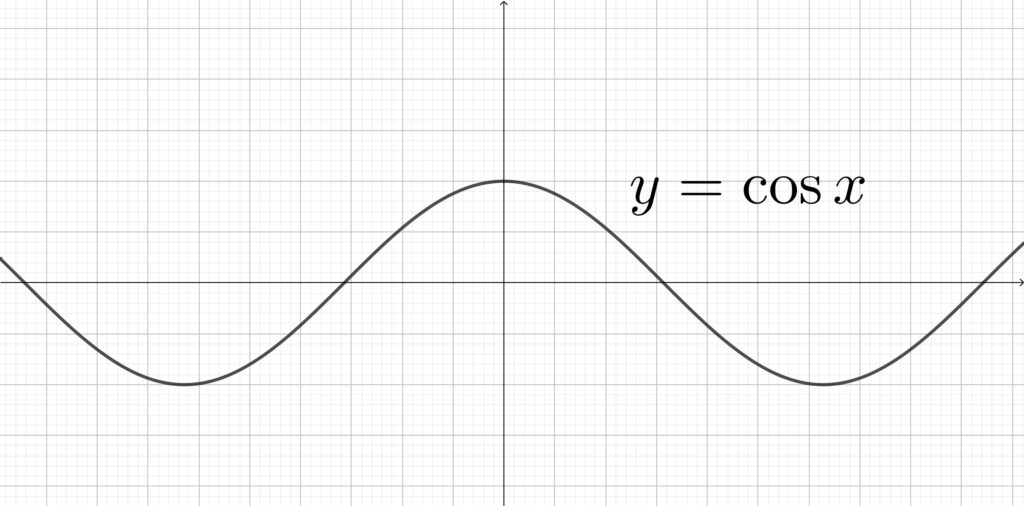 \(y=\cos{x}\) のグラフ
\(y=\cos{x}\) のグラフ
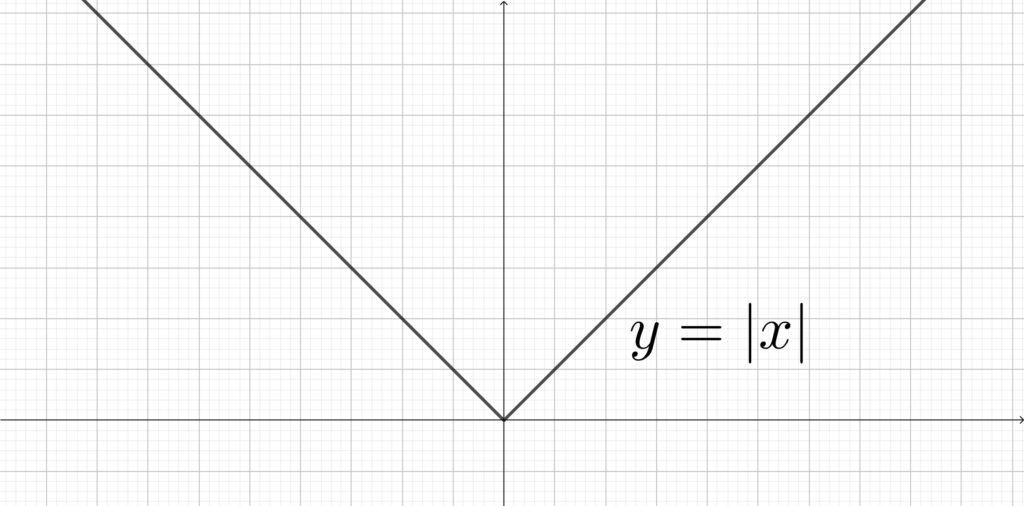 \(y=|x|\) のグラフ
\(y=|x|\) のグラフ
上図からわかるように\(,\) 偶関数のグラフはすべて \(y\) 軸対称になります.
公式の面積によるイメージ
\begin{align}\int_{-a}^af(x)dx\end{align}
という式は \(y=f(x)\) のグラフと \(x\) 軸\(,\) および \(2\) 直線 \(x=-a,~x=a\) で囲まれた部分の(符号付き)面積という意味です. 特に \(f(x)\) が奇関数\(,\) 偶関数のときは以下のような(符号付き)面積を求めることになります.
 \(f(x)\) が奇関数のとき
\(f(x)\) が奇関数のとき
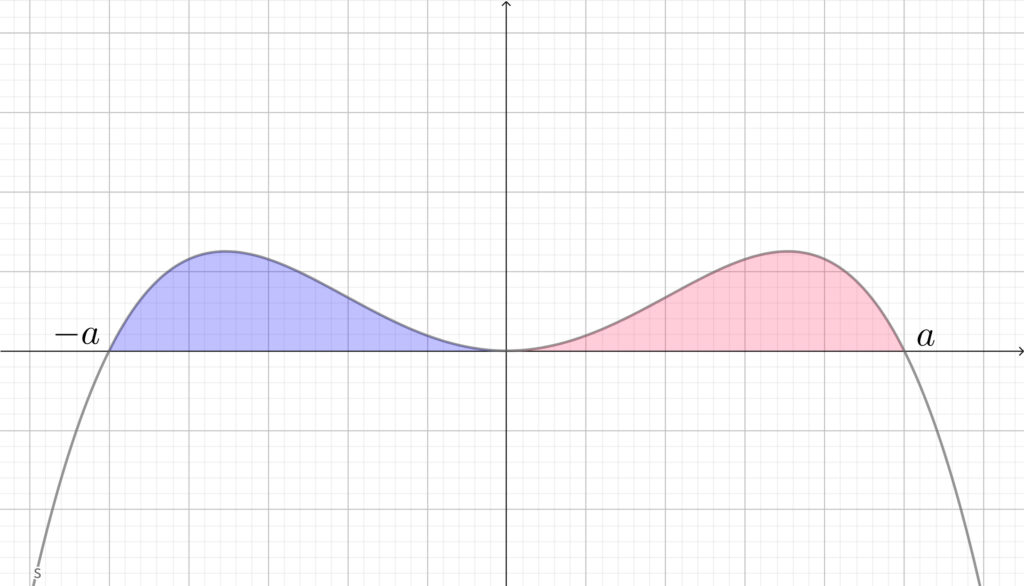 \(f(x)\) が偶関数のとき
\(f(x)\) が偶関数のとき
奇関数のグラフは原点対称\(,\) 偶関数のグラフは \(y\) 軸対称ですから\(,\) 上図の青色部分と赤色部分の面積(の絶対値)はどちらも等しくなります.
奇関数の場合は\(,\) 青色部分が \(x\) 軸より下にあるので\(,\) 面積はマイナスの値をとり\(,\)赤色部分が \(x\) 軸より上にあるので\(,\) 面積はプラスの値をとります. つまり\(,\) プラスとマイナスで相殺されて \(0\) になるというイメージになります.
偶関数の場合は\(,\) 青色部分と赤色部分のどちらも \(x\) 軸よりも上にあるので\(,\) 面積はどちらもプラスの値をとり\(,\) かつ同じ値になります. つまり\(,\) 赤色部分だけ求めて \(2\) 倍すればよいというイメージになります.
公式の証明
奇関数・偶関数いずれの場合も途中までは同じです. ポイントは区間を \(0\) で区切ることです.
\begin{align}\int_{-a}^af(x)dx=\int_{-a}^0f(x)dx+\int_0^af(x)dx\end{align}
ここ\(,\) \(x=-t\) とおくと\(,\)
\begin{align}dx=-dt\end{align}
であり\(,\)
\begin{align}\begin{array}{|c|ccc|}\hline x & -a & \to & 0 \\ \hline t & a & \to & 0\\ \hline\end{array}\end{align}
であるから\(,\) 右辺の第 \(1\) 項は\(,\)
\begin{align}\int_{-a}^0f(x)dx=\int_a^0f(-t)(-1)dt\end{align}
\begin{align}=\int_0^af(-t)dt=\int_0^af(-x)dx\end{align}

quandle
積分するときに使う文字については何でもいいのですから\(,\) \(t\) を \(x\) で置き直しています.
よって\(,\)
\begin{align}\int_{-a}^af(x)dx=\int_0^a\{f(-x)+f(x)\}dx\end{align}
\begin{align}=\left\{\begin{array}{cc}\displaystyle \int_0^a\{-f(x)+f(x)\}dx & (~f(x)~:~奇関数~)\\ \displaystyle \int_0^a\{f(x)+f(x)\}dx & (~f(x)~:~偶関数~)\end{array}\right.\end{align}
\begin{align}=\left\{\begin{array}{cc} 0 & (~f(x)~:~奇関数~)\\ \displaystyle 2\int_0^af(x)dx & (~f(x)~:~偶関数~)\end{array}\right.\end{align}
練習問題〜理科大の過去問に挑戦〜
山口東京理科大学 工学部前期2020年第1問(2)
山口東京理科大学 工学部中期2020年第4問
諏訪東京理科大学 中期2020年第3問


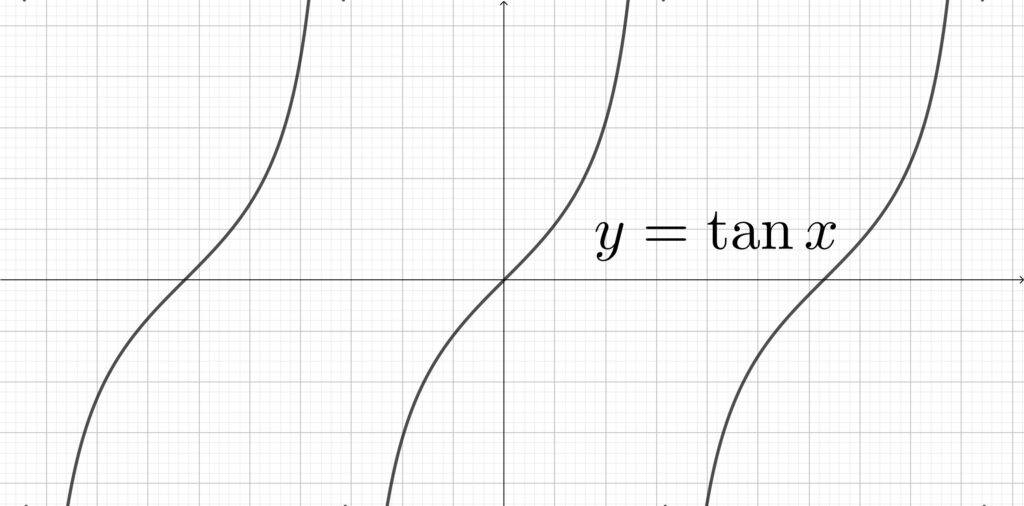












2022年第3問-120x68.jpg)
コメント