経営学部(共通問題)2023年第2問の問題文全文
\(a,~b,~c,~d\) を実数とし\(,\) \(f(x)=ax^3+bx^2+cz+d\) とおく. 関数 \(f(x)\) は \(x=-1\) と \(x=1\) で極値をとり\(,\) 曲線 \(y=f(x)\) は \(2\) 点 \(\displaystyle \left(0,~\frac{1}{2}\right),~\left(\frac{1}{2},~0\right)\) を通るとする. このとき\(,\) 次の問に答えよ.
(1) \(a,~b,~c,~d\) の値を求めよ.
(2) 関数 \(f(x)\) の極大値と極小値の差の絶対値を求めよ.
(3) \(2\) 点 \((-1,~f(-1)),~(1,~f(1))\) を通る直線の方程式を \(y=g(x)\) とする. \(g(x)\) を求め\(,\) 曲線 \(y=f(x)\) と直線 \(y=g(x)\) で囲まれた部分の面積 \(S\) を求めよ.
(1) の着眼点〜極値をもつ条件〜
未知数の数は \(a,~b,~c,~d\) の \(4\) つですので\(,\) 式を \(4\) 本立てる必要があります.
そのうちの \(2\) つは\(,\) \(2\) 点 \(\displaystyle \left(0,~\frac{1}{2}\right),~\left(\frac{1}{2},~0\right)\) を通ることから\(,\)
です.
微分可能な関数 \(f(x)\) が \(x=\alpha \) で極値をもつための必要十分条件は以下の \(2\) 条件を同時に満たすことである.
① \(f^{\prime}(\alpha )=0\)
② \(x=\alpha \) の十分近くで \(f^{\prime}(x)\) の符号が変化する
残りの \(2\) つは \(x=-1,~1\) で極値をとることから\(,\) 上記の①より\(,\)
です. これで \(4\) つ揃いました. これで \(a,~b,~c,~d\) が求められますね!
(1) の解答〜 \(a,~b,~c,~d\) が出ても油断しない〜
\(\displaystyle f(0)=\frac{1}{2}\) より\(,\)
このとき\(,\)
\(\displaystyle f\left(\frac{1}{2}\right)=0\) より\(,\)
\(f^{\prime}(x)=3ax^2+2bx+c\) であるから\(,\)
\(f^{\prime}(-1)=0\) より\(,\)
\(f^{\prime}(1)=0\) より\(,\)
①\(,\) ②\(,\) ③\(,\) ④を解いて\(,\)
このとき\(,\)
となるから\(,\) 増減表は以下のようになる.
増減表より\(,\) \(f(x)\) は \(x=-1\) のときに極大値\(,\) \(x=1\) のときに極小値を取っているため\(,\) 問題に適している. したがって\(,\)

\(f^{\prime}(x)\) が \(x=\pm 1\) の十分近くで符号が変わっていることを必ずチェックしましょう!
(2) の解答〜サービス問題〜
(1) より\(,\) 極大値は \(\displaystyle \frac{27}{22}\)\(,\) 極小値は \(\displaystyle -\frac{5}{22}\) であるから\(,\)
(3) の解答〜曲線と直線の上下関係に注意〜
\(g(x)\) を求める〜 \(2\) 点の中点がちょうど \(y\) 切片であることに注目〜
\(y=g(x)\) は \(2\) 点 \(\displaystyle \left(-1,~\frac{27}{22}\right),~\left(1,~-\frac{5}{22}\right)\) を通る直線であり\(,\) \(2\) 点の中点 \(\displaystyle \left(0,~\frac{1}{2}\right)\) は \(y\) 切片になるから\(,\)

極大と極小の \(x\) 座標の絶対値が同じであることに注目すると\(,\) 中点の \(x\) 座標が \(0\) なので\(,\) \(y\) 切片の \(y\) 座標が即わかりますね. また\(,\) \(f(x)\) は \(3\) 次関数なので\(,\) この中点は \(3\) 次関数上の点でもあります.
\(S\) を求める〜対称性に注目して計算量を減らす〜
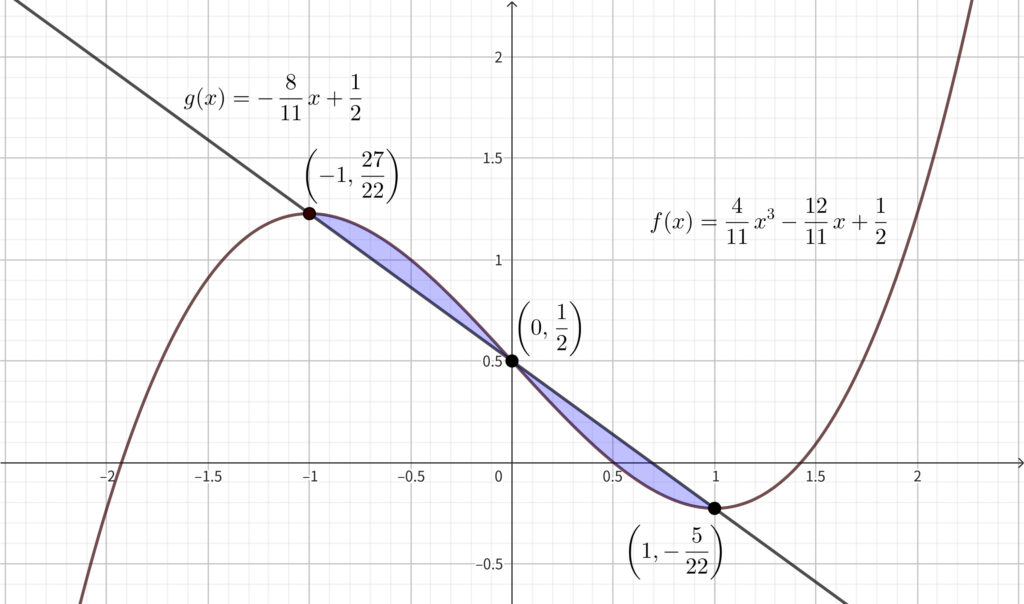
点 \(\displaystyle \left(0,~\frac{1}{2}\right)\) に関して\(,\) \(y=f(x)\) と \(y=g(x)\) は点対称になる. 上図より\(,\) 求める面積 \(S\) は




コメント