東京理科大学創域理工学部（数理・先物・情計・生生・経シス）2023年第３問

創域理工学部（数理・先物・情計・生生・経シス）2023年第３問の問題分全文

座標平面上で$,$ 直線 $y=\sqrt{5}\log{x}~(x>0)$ を $C$ とし$,$ $C$ 上に点 $\mathrm{A}(a,~\sqrt{5}\log{a})~(a>0)$ をとる. ただし$,$ $\log$ は自然対数とする. 点 $\mathrm{A}$ における $C$ の接線を $\ell$ とし$,$ $\ell$ と $y$ 軸の交点を $\mathrm{Q}(0,~q)$ とする. また$,$ 点 $\mathrm{A}$ における $C$ の法線を $m$ とし$,$ $m$ と $y$ 軸の交点を $\mathrm{R}(0,~r)$ とする.

(1) $q$ を$,$ $a$ を用いて表せ.

(2) $r$ を$,$ $a$ を用いて表せ.

(3) 線分 $\mathrm{QR}$ の長さが $3\sqrt{5}$ になるような $a$ の値を求めよ.

(4) $\displaystyle \angle \mathrm{ARQ}=\frac{\pi}{6}$ となるような $a$ の値を求めよ.

(5) $a=e^2$ とする. このとき$,$ $x$ 軸$,$ 曲線 $C$ および直線 $\ell$ で囲まれた部分の面積を求めよ. ただし$,$ $e$ は自然対数の底である.

(1) の解答〜接線を求める〜

$\displaystyle y^{\prime}=\frac{\sqrt{5}}{x}$ より$,$ 接線 $\ell$ は$,$

$x=0,~y=q$ のとき$,$

(2) の解答〜法線の傾きは「傾きかけて $-1$ 」で求める〜

$\ell \perp m$ より$,$ 法線 $m$ の傾きは $\displaystyle -\frac{a}{\sqrt{5}}$ であるから$,$

$x=0,~y=r$ のとき$,$

(3) の解答〜 $y$ 座標の差で $\mathrm{QR}$ を求める〜

$\mathrm{QR}=3\sqrt{5}$ より$,$

$a>0$ より$,$

(4) の解答〜傾きはなす角の $\tan$ に等しい〜

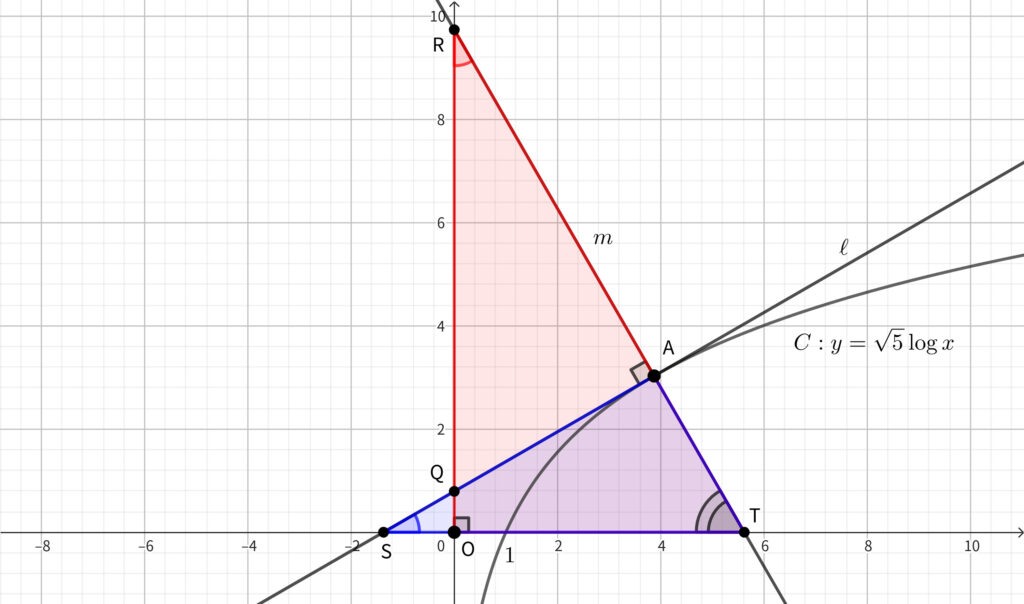
上図のように $,$ $x$ 軸と$,$ $\ell$ および $m$ との交点をそれぞれ $\mathrm{S},~\mathrm{T}$ とおくと$,$

$\triangle \mathrm{TOR}$ と $\triangle \mathrm{TAS}$ は $\angle \mathrm{RTO}=\angle \mathrm{STA}$ が共通していることから相似であるから$,$

よって$,$ $\ell$ の傾きが $\displaystyle \tan{\frac{\pi}{6}}$ に一致するので$,$

(5) の解答〜大きな三角形からくり抜く〜

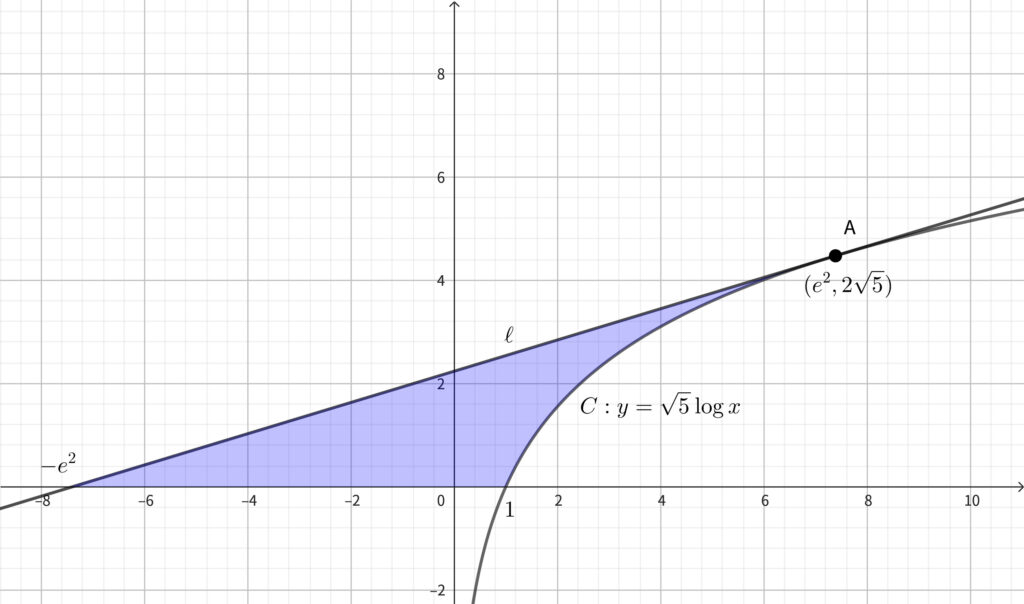
上図の青色部分の面積を求めればよい. そのためには下図の赤色部分の面積から緑色部分の面積を引けばよい.

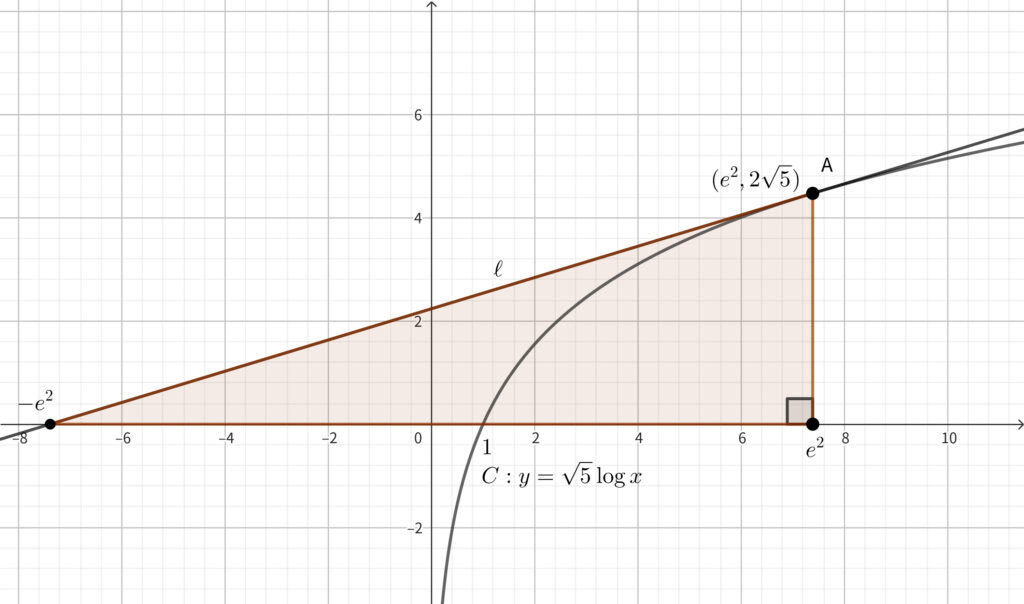
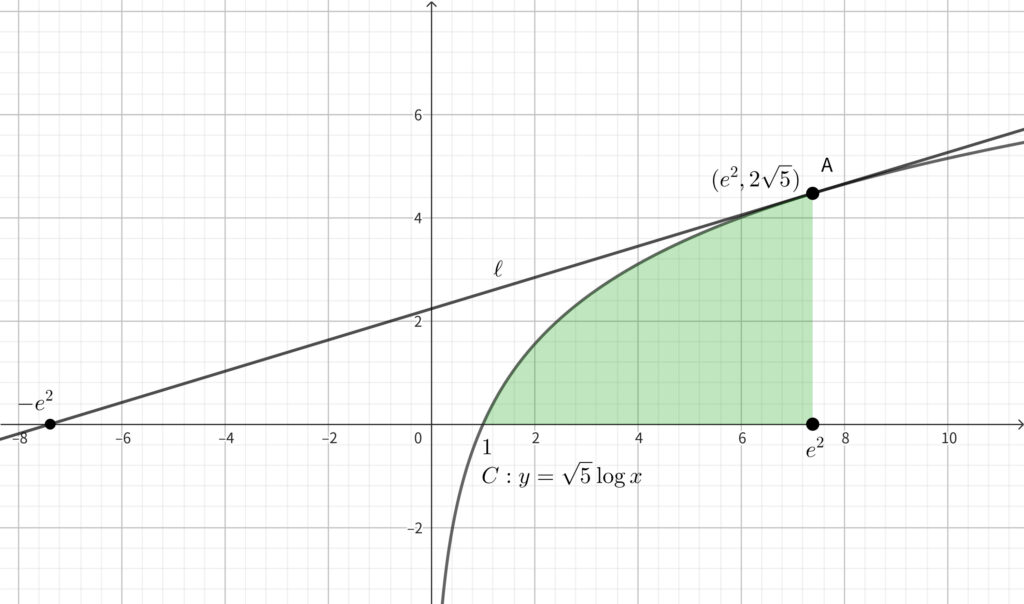
求める面積は$,$