理学部(共通)2023年第3問の問題文全文
\(\displaystyle f(x)=-\frac{\sin{x}}{2+\cos{x}}\) と \(\displaystyle g(x)=\frac{\cos{x}}{2+\sin{x}}\) に対して以下の問いに答えよ.
(1) 不定積分 \(\displaystyle \int f(x)dx\) と \(\displaystyle \int g(x)dx\) を計算せよ.
(2) すべての実数 \(x\) に対して \(f(x)=g(x+s)\) が成り立つような\(,\) 正の実数 \(s~(0<s<2\pi )\) の値を求めよ.
(3) \(0\leqq x \leqq 2\pi \) のとき\(,\) \(f(x)\) と \(g(x)\) のそれぞれについて最大値と最小値\(,\) およびそれらを与える \(x\) の値を求めよ.
(4) \(f(x)=g(x)\) を満たす正の実数 \(x\) の中で最小の数を \({\alpha}_1\)\(,\) \(2\) 番目に小さい数を \({\alpha}_2\) とする. \({\alpha}_1+{\alpha}_2\) の値を求めよ.
(5) 座標平面において\(,\) \(2\) 曲線 \(y=f(x)~(0\leqq x \leqq 2\pi )\) と \(y=g(x)~(0\leqq x \leqq 2\pi )\) で囲まれた図形の面積を求めよ.
(1) の解答〜 \(\displaystyle \frac{y^{\prime}}{y}\) の形は暗算で!〜
\begin{align}\int -\frac{\sin{x}}{2+\cos{x}}dx=\int \frac{(2+\cos{x})^{\prime}}{2+\cos{x}}dx\end{align}
\begin{align}=\log{(2+\cos{x})}+C~(~C~は積分定数)~~~~\cdots \fbox{答}\end{align}
\begin{align}\int \frac{\cos{x}}{2+\sin{x}}dx=\int \frac{(2+\sin{x})^{\prime}}{2+\sin{x}}dx\end{align}
\begin{align}=\log{(2+\sin{x})}+C~(~C~は積分定数)~~~~\cdots \fbox{答}\end{align}

quandle
本来 \(\displaystyle \int \frac{y^{\prime}}{y}dx=\log{|y|}+C\) ですから\(,\) 絶対値をつけないといけませんが\(,\) 今回は絶対値を外せます. なぜなら\(,\) \(\sin{x}\geqq -1,~\cos{x}\geqq -1\) より\(,\) \(2+\sin{x}>0,~2+\cos{x}>0\) だからです.
(2) の解答〜全称命題は必要条件から攻める〜
全称命題とは?
「すべての○○に対して△△が成り立つ」
の形の命題を「全称命題」と言います. 全称命題の攻め方は
① 「自分にとって都合のよいもの」を代入などして答えの候補を絞る(必要条件を求める)
② 十分性が成り立つかを確認する
の2ステップを踏めばOKです.
今回であれば\(,\)
「すべての実数 \(x\) に対して \(f(x)=g(x+s)\) が成り立つ」
と言っていますから全称命題です. 「自分にとって都合のよい(=今回であれば計算が楽という意味)」な \(x=0\) を代入してみましょう. すべての \(x\) で成り立つのですから \(x=0\) でも成り立つはずです.
ただし\(,\) \(x=0\) を代入して得られる \(s\) の値はあくまでも候補です. もしかしたら \(x=\pi \) などでは成り立たないかもしれません. そのため\(,\) 得られた \(s\) であればすべての \(x\) でも成り立つこと(十分性)をあわせて示す必要があります.
必要条件を求める
\(x=0\) のときも \(f(0)=g(0+s)\) が成り立つ必要がある.
\begin{align}f(0)=0,~g(0+s)=\frac{\cos{s}}{2+\sin{s}}\end{align}
より\(,\) \(f(0)=g(0+s)\) のとき\(,\)
\begin{align}\cos{s}=0\end{align}
\begin{align}s=\frac{\pi}{2}~\mathrm{or}~\frac{3}{2}\pi \end{align}
十分性を示す
\(\displaystyle s=\frac{\pi}{2}\) のとき\(,\) すべての実数 \(x\) に対して\(,\)
\begin{align}g\left(x+\frac{\pi}{2}\right)=\cfrac{\cos{\left(x+\cfrac{\pi}{2}\right)}}{2+\sin{\left(x+\cfrac{\pi}{2}\right)}}\end{align}
\begin{align}=\frac{-\sin{x}}{2+\cos{x}}=f(x)\end{align}
が成り立つので十分性も示された.
\(\displaystyle x=\frac{3}{2}\pi\) のとき\(,\)
\begin{align}g\left(x+\frac{3}{2}\pi\right)=\cfrac{\cos{\left(x+\cfrac{3}{2}\pi \right)}}{2+\sin{\left(x+\cfrac{3}{2}\pi \right)}}\end{align}
\begin{align}=\frac{\sin{x}}{2-\cos{x}}\neq f(x)\end{align}
となるため\(,\) 十分性は成り立たない. 以上より\(,\)
\begin{align}s=\frac{\pi}{2}~~~~\cdots \fbox{答}\end{align}
(2) の主張〜\(f(x)\) と \(g(x)\) の関係は?〜
\begin{align}f(x)=g\left(x+\frac{\pi}{2}\right)\end{align}
から\(,\)
\(y=f(x)\) のグラフを \(x\) 軸方向に \(\displaystyle \frac{\pi}{2}\) だけ平行移動したもの
になっていることがわかります.
(3) の解答〜(2) の主張を利用〜
\begin{align}f^{\prime}(x)=\frac{-\cos{x}(2+\cos{x})+\sin{x}(-\sin{x})}{(2+\cos{x})^2}\end{align}
\begin{align}=\frac{-2\cos{x}-1}{(2+\cos{x})^2}\end{align}
\((2+\cos{x})^2>0\) であるから\(,\) \(-2\cos{x}-1\) の符号と \(f^{\prime}(x)\) の符号は一致する.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle \frac{2}{3}\pi & \cdots & \displaystyle \frac{4}{3}\pi & \cdots & 2\pi \\ \hline f^{\prime}(x) & {} & – & 0 & + & 0 & – & {} \\ \hline f(x) & 0 & \searrow & \displaystyle -\frac{\sqrt{3}}{3} & \nearrow & \displaystyle \frac{\sqrt{3}}{3} & \searrow & 0 \\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}x=\frac{2}{3}\pi~のとき~f(x)~の最小値~-\frac{\sqrt{3}}{3}~~~~\cdots \fbox{答}\end{align}
\begin{align}x=\frac{4}{3}\pi~のとき~f(x)~の最大値~\frac{\sqrt{3}}{3}~~~~\cdots \fbox{答}\end{align}
(2) より\(,\) \(y=g(x)\) のグラフは\(,\) \(y=f(x)\) のグラフを \(x\) 軸方向に \(\displaystyle \frac{\pi}{2}\) だけ平行移動したものであるから\(,\)
\begin{align}x=\frac{2}{3}\pi +\frac{\pi}{2}=\frac{7}{6}\pi~のとき~g(x)~の最小値~-\frac{\sqrt{3}}{3}~~~~\cdots \fbox{答}\end{align}
\begin{align}x=\frac{4}{3}\pi +\frac{\pi}{2}=\frac{11}{6}\pi~のとき~g(x)~の最小値~\frac{\sqrt{3}}{3}~~~~\cdots \fbox{答}\end{align}
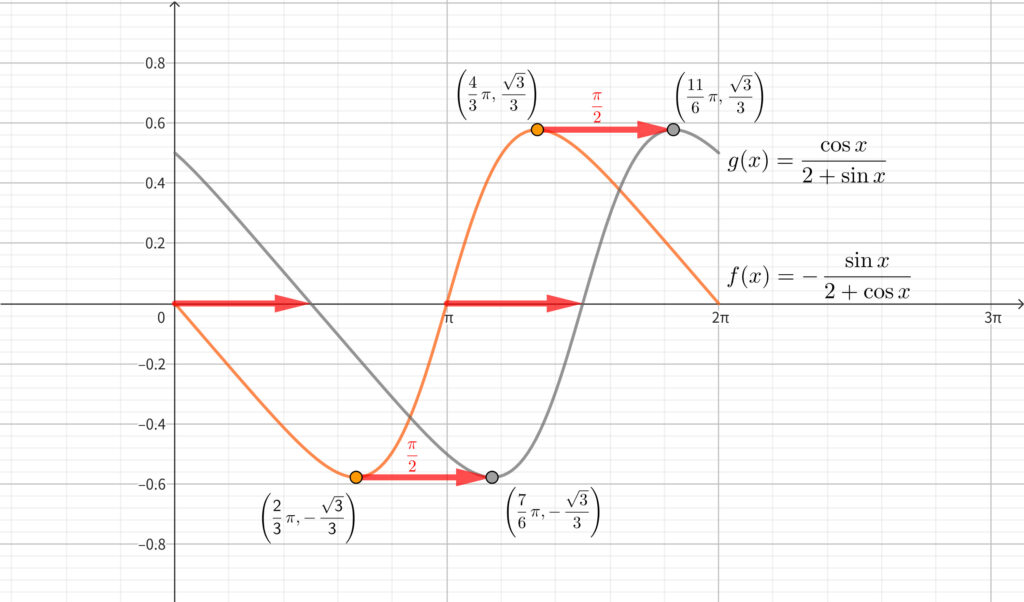
※ \(y=f(x)\) のグラフと \(y=g(x)\) のグラフの位置関係は上図のようになります.
(3) の解答〜\(\alpha_1\) と \(\alpha_2\) を直接求めることはできない〜
求めたい \(\alpha_1 +\alpha_2 \) のイメージ
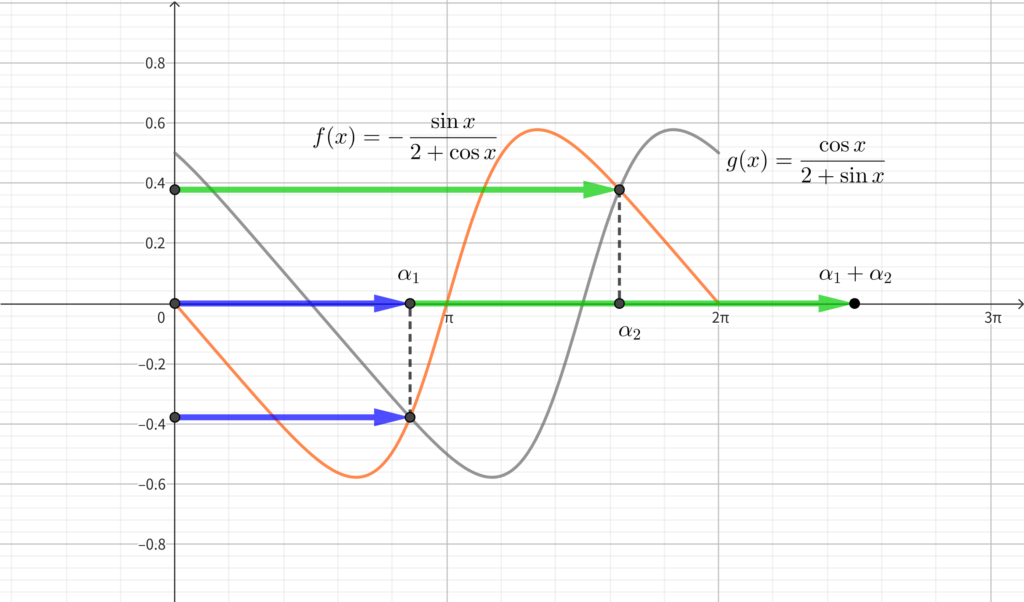
青い矢印は \(\alpha_1\) の長さを表し\(,\) 緑の矢印は \(\alpha_2\) の長さを表している.
\(\alpha_1 +\alpha_2\) は青い矢印と緑の矢印を足した長さになっている.
\(f(x)=g(x)\) を解く〜三角関数の合成〜
\begin{align}f(x)=g(x)\Leftrightarrow -\frac{\sin{x}}{2+\cos{x}}=\frac{\cos{x}}{2+\sin{x}}\end{align}
\begin{align}\Leftrightarrow -\sin{x}(2+\sin{x})=\cos{x}(2+\cos{x})\end{align}
\begin{align}\Leftrightarrow -2\sin{x}-\sin^2{x}=2\cos{x}+\cos^2{x}\end{align}
\begin{align}\Leftrightarrow 2\sin{x}+2\cos{x}=-1\end{align}
\begin{align}\Leftrightarrow 2\sqrt{2}\sin{\left(x+\frac{\pi}{4}\right)}=-1\end{align}
\begin{align}\Leftrightarrow \sin{\left(x+\frac{\pi}{4}\right)}=-\frac{1}{2\sqrt{2}}\end{align}
\(\alpha_1 ,~\alpha_2\) はこの等式を満たす. 単位円上に図示すると下図のようになる.
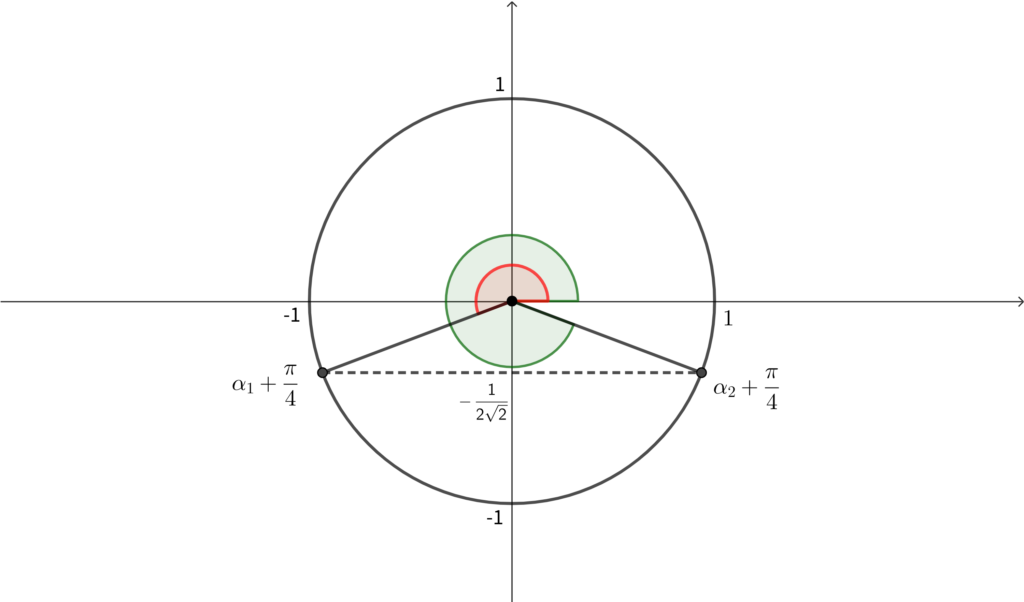
上図より\(,\)
\begin{align}\left(\alpha_1 +\frac{\pi}{4}\right)+\left(\alpha_2 +\frac{\pi}{4}\right)=3\pi\end{align}
\begin{align}\therefore \alpha_1 +\alpha_2 =\frac{5}{2}\pi~~~~\cdots \fbox{答}\end{align}

quandle
赤い部分と緑の部分の和を考えます. 赤い部分を \(\pi +\theta \) とすると\(,\) 緑色の部分は \(2\pi -\theta \) とかけます. よって和は
\begin{align}(\pi +\theta)+(2\pi -\theta)=3\pi\end{align}
となります.
(5) の解答〜(4) を用いて一文字消去〜
準備①〜\(\sin{\alpha_2},~\cos{\alpha_2}\) を\(\alpha_1\) で表す〜
(4) より\(,\) \(\displaystyle \alpha_1 +\alpha_2=\frac{5}{2}\pi\) であるから\(,\)
\begin{align}\alpha_2=\frac{5}{2}\pi-\alpha_1\end{align}
とかける. このとき\(,\)
\begin{align}\sin{\alpha_2}=\sin{\left(\frac{5}{2}\pi -\alpha_1\right)}=\cos{\alpha_1}\end{align}
\begin{align}\cos{\alpha_2}=\cos{\left(\frac{5}{2}\pi -\alpha_1\right)}=\sin{\alpha_1}\end{align}
準備②〜\(\sin{\alpha_1},~\cos{\alpha_1}\) を求める〜
(4) より\(,\) \(\alpha_1\) は
\begin{align}\sin{x}+\cos{x}=-\frac{1}{2}\end{align}
の解である. 両辺を \(2\) 乗して\(,\)
\begin{align}1+2\sin{x}\cos{x}=\frac{1}{4}\end{align}
\begin{align}\sin{x}\cos{x}=-\frac{3}{8}\end{align}
を得る.
\begin{align}\sin{\alpha_1}+\cos{\alpha_1}=-\frac{1}{2},~\sin{\alpha_1}\cos{\alpha_1}=-\frac{3}{8}\end{align}
であるから\(,\) \(\sin{\alpha_1},~\cos{\alpha_1}\) は \(2\) 次方程式
\begin{align}t^2+\frac{1}{2}t-\frac{3}{8}=0\end{align}
の解である. これを解いて\(,\)
\begin{align}t=\frac{-1\pm \sqrt{7}}{4}\end{align}
を得る. ここで\(,\)(4) より\(,\)
\begin{align}\sin{\left(\alpha_1 +\frac{\pi}{4}\right)}=-\frac{1}{2\sqrt{2}}>-\frac{1}{\sqrt{2}}=\sin{\frac{5}{4}\pi}\end{align}
であるから\(,\) \(\displaystyle \frac{\pi}{2}<\alpha_1 <\pi \) であることが示された.
よって\(,\) \(\sin{\alpha_1}>0,~\cos{\alpha_1}<0\) であるから\(,\)
\begin{align}\sin{\alpha_1}=\frac{-1+\sqrt{7}}{4},~\cos{\alpha_1}=\frac{-1-\sqrt{7}}{4}\end{align}
面積を求める〜面積は(上の式)ー(下の式)〜
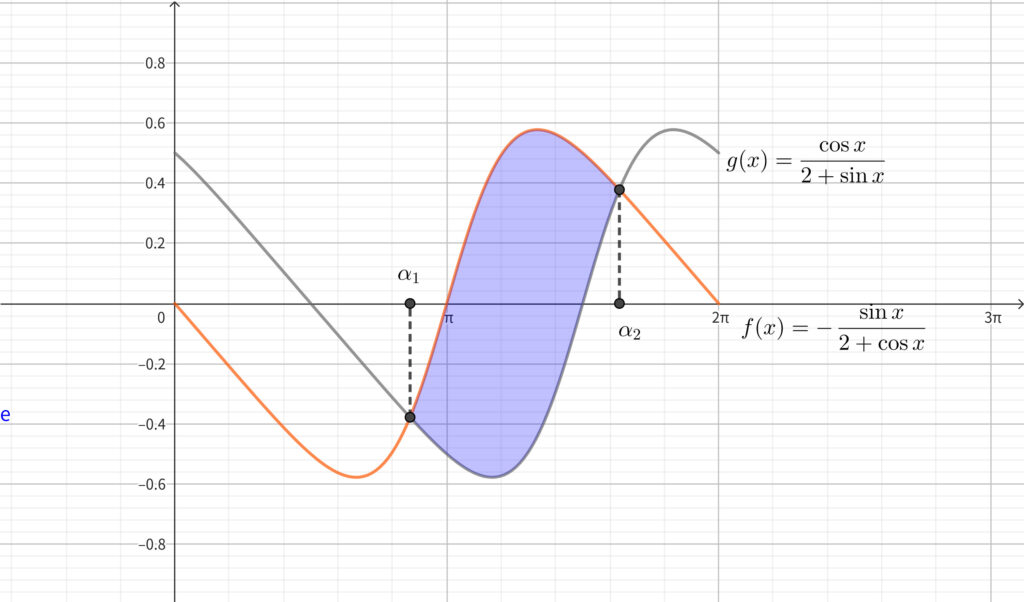
求める面積を \(S\) とおく. 上図より\(,\)
\begin{align}S=\int_{\alpha_1}^{\alpha_2}(f(x)-g(x))dx\end{align}
\begin{align}=\biggl[\log{(2+\cos{x})}-\log{(2+\sin{x})}\biggr]_{\alpha_1}^{\alpha_2}\end{align}
\begin{align}=\log{(2+\cos{\alpha_2})}-\log{(2+\sin{\alpha_2})}-\log{(2+\cos{\alpha_1})}+\log{(2+\sin{\alpha_1})}\end{align}
\begin{align}=\log{(2+\sin{\alpha_1})}-\log{(2+\cos{\alpha_1})}-\log{(2+\cos{\alpha_1})}+\log{(2+\sin{\alpha_1})}\end{align}
\begin{align}=2\log{\frac{2+\sin{\alpha_1}}{2+\cos{\alpha_1}}}=2\log{\cfrac{2+\cfrac{-1+\sqrt{7}}{4}}{2+\cfrac{-1-\sqrt{7}}{4}}}\end{align}
\begin{align}=2\log{\frac{7+\sqrt{7}}{7-\sqrt{7}}}=2\log{\frac{\sqrt{7}+1}{\sqrt{7}-1}}\end{align}
\begin{align}=2\log{\frac{8+2\sqrt{7}}{6}}=2\log{\frac{4+\sqrt{7}}{3}}~~~~\cdots \fbox{答}\end{align}










コメント