公立諏訪東京理科大学 中期 2023年第1問の問題文全文
\(a>0\) とし\(,\) 座標平面において曲線 \(y=e^{ax}\) 上の \(x\) 座標が負である点 \(\mathrm{P}\) における接線と\(,\) 両座標軸とで囲まれる図形の面積を \(S\) とする. このとき\(,\) 以下の問いに答えよ. ただし\(,\) \(e\) は自然対数の底とする.
(1) 点 \(\mathrm{P}\) の \(x\) 座標を \(p\) とし\(,\) \(S\) を \(p\) で表せ.
(2) (1) で求めた \(S\) を \(p\) で微分せよ.
(3) \(p\) の関数 \(S\) の最大値を求めよ.
(1) の解答〜長さは絶対値で表す〜
\begin{align}y^{\prime}=ae^{ax}\end{align}
より\(,\) 点 \((p,~e^{ap})\) における接線の方程式は\(,\)
\begin{align}y=ae^{ap}(x-p)+e^{ap}\end{align}
\(x=0\) のとき\(,\)
\begin{align}y=-ape^{ap}+e^{ap}=(1-ap)e^{ap}\end{align}
より\(,\) \(y\) 切片の座標は\(,\)
\begin{align}(0,~(1-ap)e^{ap})\end{align}
\(y=0\) のとき\(,\)
\begin{align}ae^{ap}(x-p)+e^{ap}=0\end{align}
\(ae^{ap}\neq 0\) より\(,\)
\begin{align}x-p+\frac{1}{a}=0\end{align}
\begin{align}\therefore x=p-\frac{1}{a}\end{align}
より\(,\) \(x\) 切片の座標は\(,\)
\begin{align}\left(p-\frac{1}{a},~0\right)\end{align}
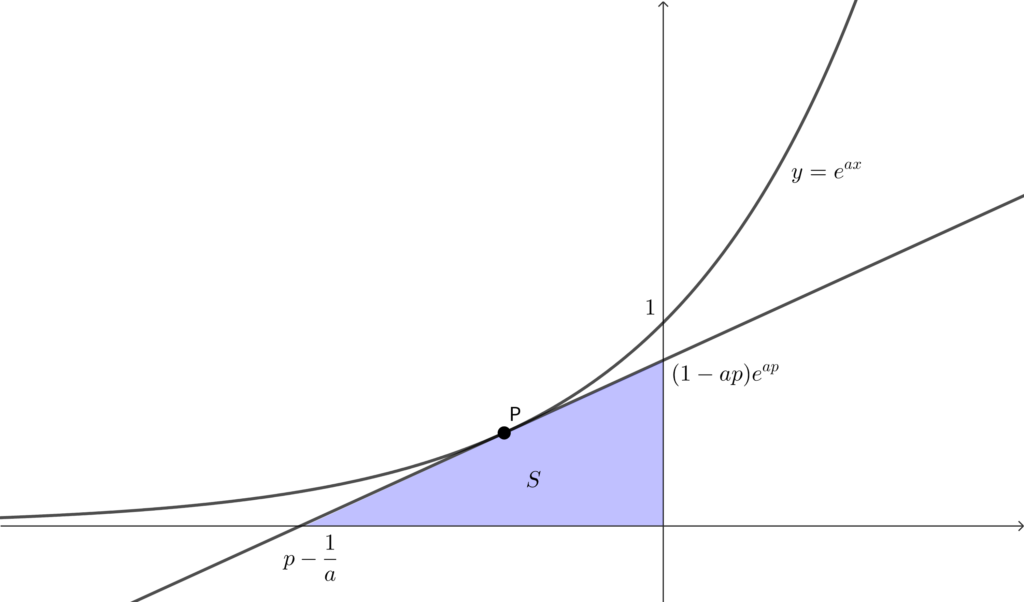
上図より\(,\) 求める面積 \(S\) は\(,\)
\begin{align}S=\frac{1}{2}\left|p-\frac{1}{a}\right|\cdot \left|(1-ap)e^{ap}\right|\end{align}
\(p<0,~a>0\) より\(,\)
\begin{align}p-\frac{1}{a}<0,~(1-ap)e^{ap}>0\end{align}
であるから\(,\)
\begin{align}S=\frac{1}{2}\left(-p+\frac{1}{a}\right)(1-ap)e^{ap}\end{align}
\begin{align}=\frac{1}{2a}(1-ap)^2e^{ap}~~~~\cdots \fbox{答}\end{align}
(2) の解答〜積の微分・合成関数の微分〜
\begin{align}\frac{dS}{dp}=\frac{1}{2a}\left\{2(1-ap)(-a)e^{ap}+(1-ap)^2\cdot ae^{ap}\right\}\end{align}
\begin{align}=\frac{1}{2}(1-ap)e^{ap}\{-2+(1-ap)\}\end{align}
\begin{align}=\frac{1}{2}(ap-1)(ap+1)e^{ap}~~~~\cdots \fbox{答}\end{align}
(3) の解答〜符号に注意〜
\(a>0,~p<0\) より\(,\)
\begin{align}\frac{1}{2}(ap-1)e^{ap}<0\end{align}
であるから\(,\) \(\displaystyle \frac{dS}{dp}\) の符号と \(ap+1\) の符号は逆符号になる. よって\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|}\hline p & \cdots & \displaystyle -\frac{1}{a} & \cdots & 0 \\ \hline \displaystyle \frac{dS}{dp} & + & 0 & – & – \\ \hline S & \nearrow & \displaystyle \frac{2}{ae} & \searrow & \displaystyle \frac{1}{2a} \\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}p=-\frac{1}{a}~のとき最大値~\frac{2}{ae}~~~~\cdots \fbox{答}\end{align}




コメント