問題文全文
\(a\) を実数, \(p,~q\) を正の実数とし, 関数 \(f(x)\) を
\begin{align}f(x)=|x-a||x-a-p||x-a-p-q|\end{align}
と定め, さらに,
\begin{align}I=\int_a^{a+p+q}f(x)dx\end{align}
と定める.
(1) \(x\) が実数全体を動くとき, \(f(x)\) を極大にする \(x\) の個数は \(\fbox{$\hskip0.8em(あ)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) 個であり, 極小にする \(x\) の個数は \(\fbox{$\hskip0.8em(い)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) 個である.
(2) \(p=q=1\) のとき,
\begin{align}I=\fbox{$\hskip0.8em(う)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
となる.
(3) 正の実数 \(p,~q\) が
\begin{align}\frac{\sqrt{3}}{3}p\leqq q\leqq \sqrt{3}p,~~p^2+q^2=1\end{align}
を満たしながら動くとする. このとき, \(t=pq\) とおいて, \(I\) を \(t\) の式で表すと
\begin{align}I=\frac{\fbox{$\hskip0.8em(え)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{12}\end{align}
となり, \(I\) のとり得る値の範囲は
\begin{align}\fbox{$\hskip0.8em(お)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\leqq I\leqq \fbox{$\hskip0.8em(か)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
となる. なお, (お)と(か)の値を導く過程を解答用紙の所定の欄に書きなさい.
(1) の着眼点
① 絶対値が 3 つもついているので慌てるかもしれません. 間違っても「それぞれを正と負の 2 つに場合分けして」などとはやってはいけません. そんなことしたら場合分けが 8 つになってしまいます.
\begin{align}|x|\cdot |y|=|xy|\end{align}
の性質を使って, 1 つの絶対値にまとめてしまいましょう.
② 関数の全体に絶対値が付いてますから, 中身の関数のグラフを描いて, \(x\) 軸よりも下側の部分を \(x\) 軸に関して折り返したグラフになります.
③ 絶対値の中身の関数は 3 次関数です. 本来は増減表をかくべきでしょうが, 穴埋め形式であること, 3 次関数のグラフは概形が決まっていることからさっとデッサンするだけに留めましょう.
(1) の解答
\begin{align}f(x)=|(x-a)(x-a-p)(x-a-p-q)|\end{align}
であるから, \(y=f(x)\) のグラフの概形は以下の実線部分である.
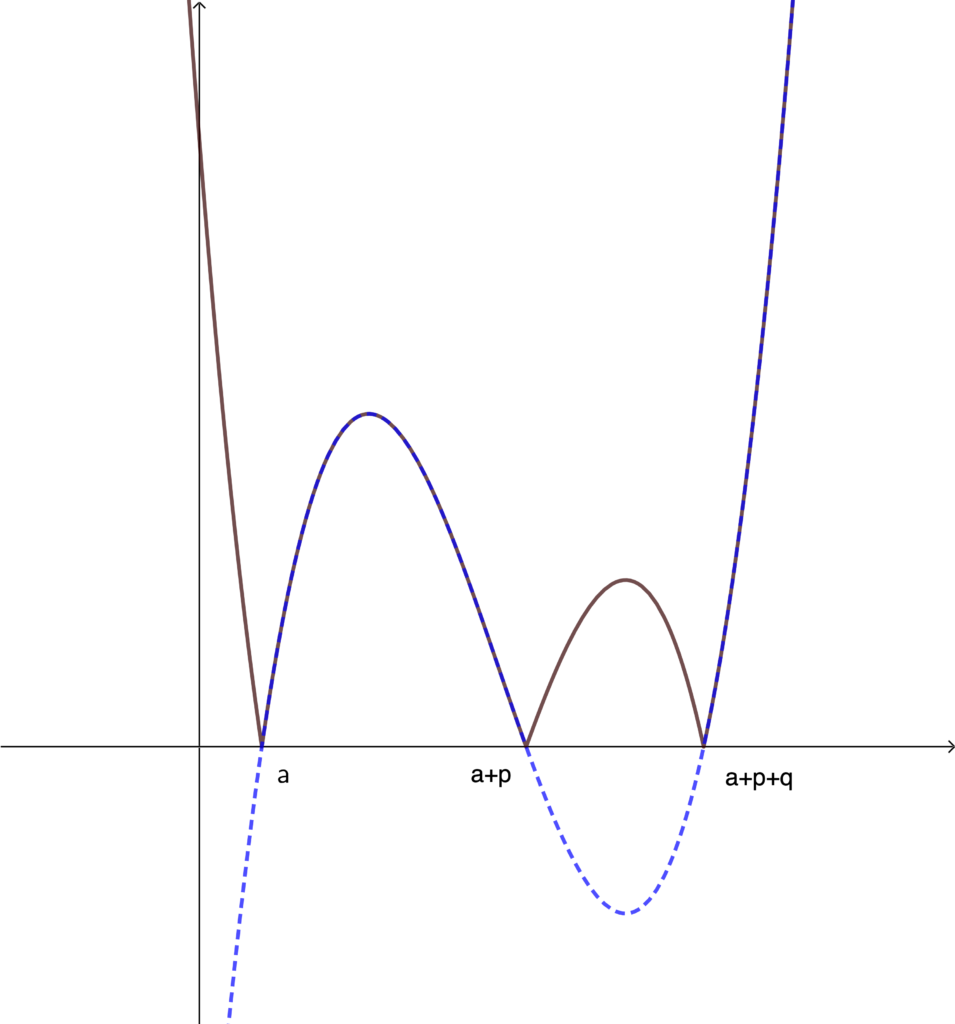
グラフより, 極大をとる \(x\) は 2 個, 極小をとる \(x\) は 3 個である.
(2) の着眼点
① \(p=q=1\) ですから, \(x\) 軸との交点が \(x=a,~x=a+1,~x=a+2\) と等間隔になります. 折り返す前の 3 次関数の変曲点が \((a+1,0)\) であることがわかります.
② 3 次関数は変曲点に関して点対称となりますから, \(a\leqq x\leqq a+1\) の部分と \(a+1\leqq x\leqq a+2\) の部分の面積は同じです. \(a\leqq x\leqq a+1\) の部分の面積を出して 2 倍しましょう.
(2) の解答
\(p=q=1\) のとき, \(y=f(x)\) のグラフは以下のようになる.
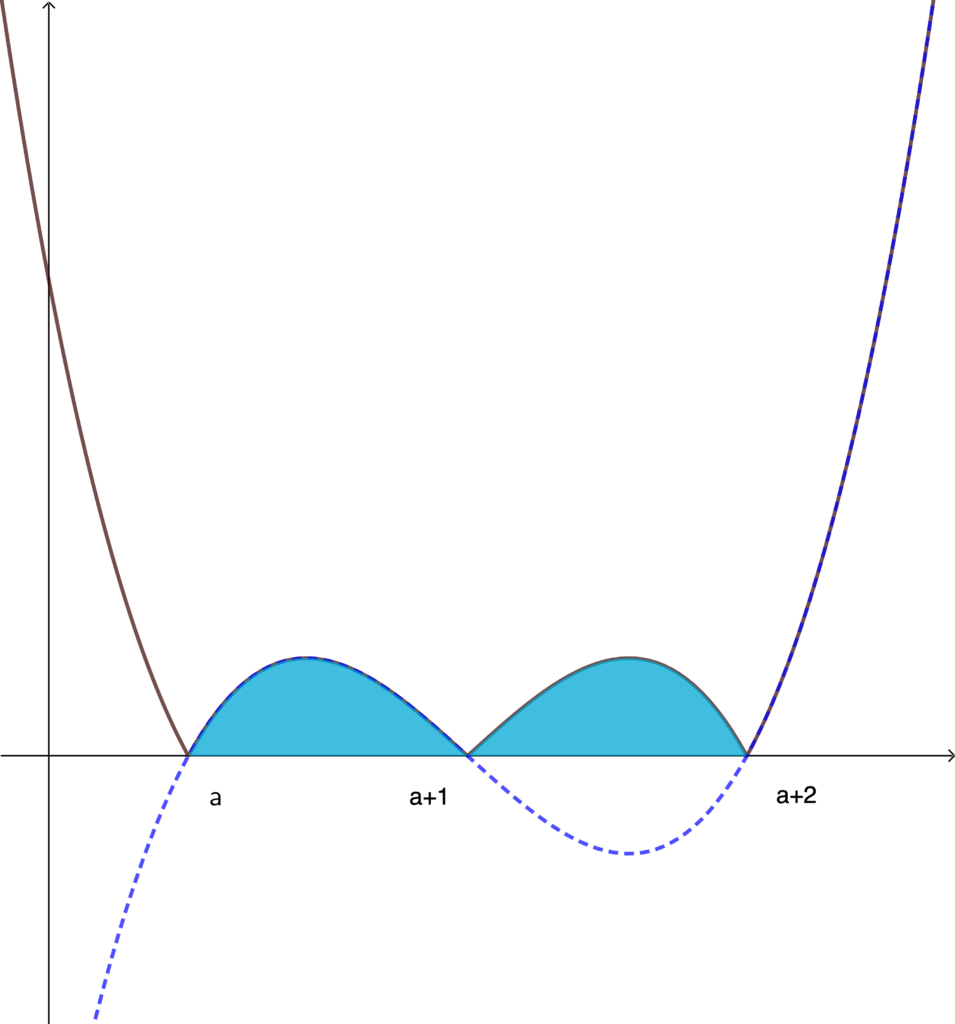
3 次関数 \(y=(x-a)(x-a-1)(x-a-2)\) は 点 \((a+1,0)\) に関して点対称であることを利用すると
\begin{align}I=\int_a^{a+2}|(x-a)(x-a-1)(x-a-2)|dx\end{align}
\begin{align}=2\int_a^{a+1}(x-a)(x-a-1)(x-a-2)dx\end{align}
\(u=x-a\) とおくと, \(\begin{array}{c|c}x & a\to a+1 \\ \hline u & 0\to 1\end{array}\) であり, \(dx=du\) であるから
\begin{align}I=2\int_0^1u(u-1)(u-2)du=2\int_0^1(u^3-3u^2+2u)du\end{align}
\begin{align}=2\biggl[\frac{1}{4}u^4-u^3+u^2\biggr]_0^1=2\left(\frac{1}{4}-1+1\right)=\frac{1}{2}.\end{align}
(3) の着眼点
① \(\displaystyle \frac{\sqrt{3}}{3}=\tan \frac{\pi}{6},~\sqrt{3}=\tan \frac{\pi}{3}\) であることから, \((p,~q)\) の存在範囲は以下の図の赤線部分になります.
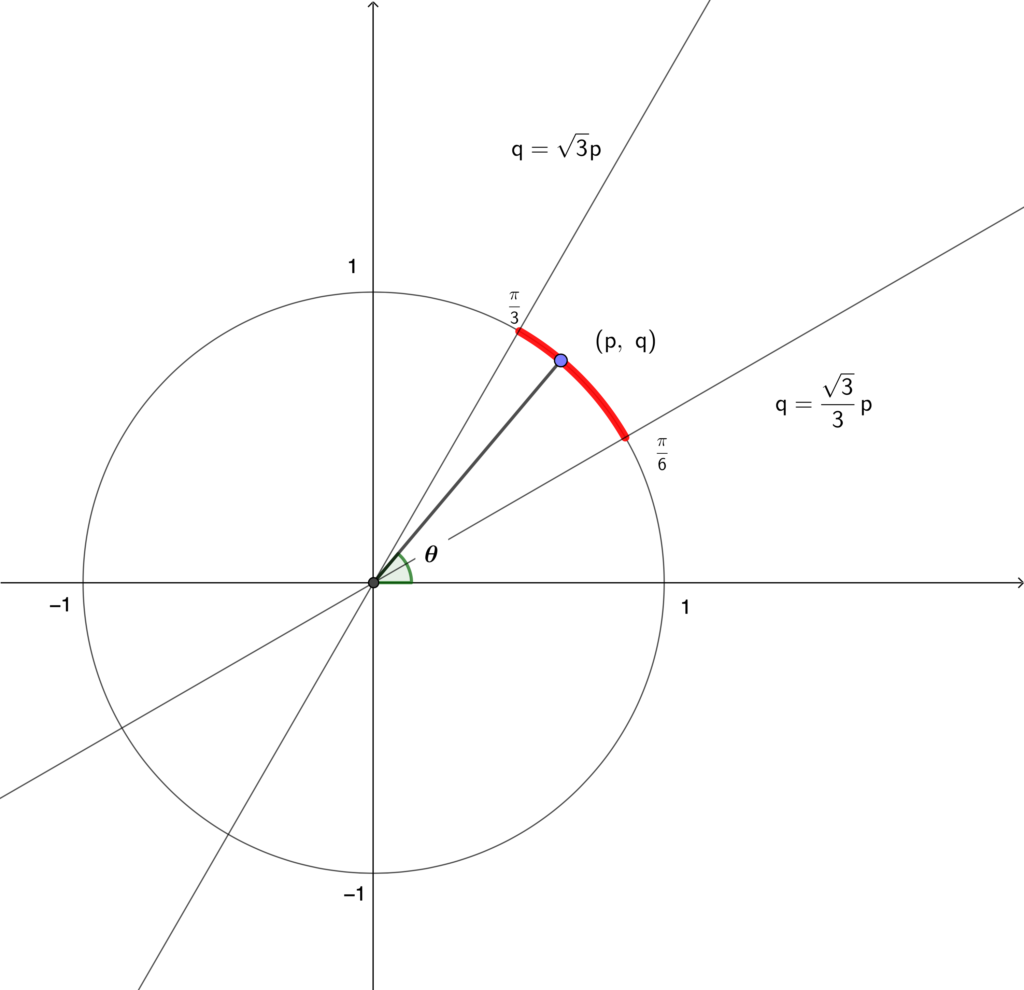
\((p,~q)\) は単位円周上の点ですから, \(p=\cos \theta,~q=\sin \theta\) とおけます.
\(\theta\) は \(\displaystyle \frac{\pi}{6}\leqq \theta \leqq \frac{\pi}{3}\) を動きます.
つまり, \(t=pq=\cos \theta \sin \theta\) は \(\theta\) の関数として考えることができます.
② (1) のグラフから, \(a\leqq x\leqq a+p\) と \(a+p\leqq x\leqq a+p+q\) に分けて積分計算することになります. 文字が多く式が長いので, うまく置換して式を短く計算しやすくしたいところです.
(3) の解答
\begin{align}I=\int_a^{a+p}(x-a)(x-a-p)(x-a-p-q)dx-\int_{a+p}^{a+p+q}(x-a)(x-a-p)(x-a-p-q)dx\end{align}
\(u=x-a\) とおくと, \begin{array}{c|c}x & a\to a+p \to a+p+q\\ \hline u & 0\to p \to p+q \end{array} であり, \(dx=du\) であるから,
\begin{align}I=\int_0^pu(u-p)(u-p-q)du-\int_p^{p+q}u(u-p)(u-p-q)du\end{align}
ここで,
\begin{align} J=\int_0^pu(u-p)(u-p-q)du,~K=\int_p^{p+q}u(u-p)(u-p-q)du\end{align}
とおく.
\begin{align}J=\int_0^p\{u^3-(2p+q)u^2+p(p+q)u\}du\end{align}
\begin{align}=\biggl[\frac{1}{4}u^4-\frac{2p+q}{3}u^3+\frac{p(p+q)}{2}u^2\biggr]_0^p=\frac{1}{4}p^4-\frac{2p+q}{3}p^3+\frac{p(p+q)}{2}p^2\end{align}
\begin{align}=\frac{1}{12}p^4+\frac{q}{6}p^3\end{align}
\(s=u-p\) とおくと, \begin{array}{c|c}u & p\to p+q \\ \hline s & 0\to q \end{array} であり, \(du=ds\) であるから,
\begin{align}K=\int_0^q(s+p)s(s-q)ds\end{align}
\begin{align}=\int_0^q\{s^3+(p-q)s^2-pqs\}ds=\biggl[\frac{1}{4}s^4+\frac{p-q}{3}s^2-\frac{pq}{2}s^2\biggr]_0^q\end{align}
\begin{align}=\frac{1}{4}q^4+\frac{p-q}{3}q^3-\frac{pq}{2}q^2=-\frac{1}{12}q^4-\frac{p}{6}q^3\end{align}
よって, \(p^2+q^2=1,~t=pq\) に注意して,
\begin{align}I=J-K=\frac{1}{12}p^4+\frac{1}{12}q^4+\frac{q}{6}p^3+\frac{p}{6}q^3\end{align}
\begin{align}=\frac{1}{12}\{(p^2+q^2)^2-2(pq)^2\}+\frac{pq}{6}(p^2+q^2)=\frac{1}{12}(1-2t^2)+\frac{t}{6}\end{align}
\begin{align}=-\frac{1}{6}t^2+\frac{1}{6}t+\frac{1}{12}=\frac{-2t^2+2t+1}{12}.\end{align}
ここで, \(\displaystyle p=\cos \theta,~q=\sin \theta~~\left(\frac{\pi}{6}\leqq \theta \leqq \frac{\pi}{3}\right)\) とおくと,
\begin{align}t=pq=\sin \theta \cos \theta=\frac{1}{2}\sin 2\theta\end{align}
\(\displaystyle \frac{\pi}{3}\leqq 2\theta \leqq \frac{2}{3}\pi\) より,
\begin{align}\frac{\sqrt{3}}{2}\leqq \sin 2\theta \leqq 1\Leftrightarrow \frac{\sqrt{3}}{4}\leqq t\leqq \frac{1}{2}\end{align}
であり, \(\displaystyle I=\cfrac{-2\left(t-\cfrac{1}{2}\right)^2+\cfrac{3}{2}}{12}\) であるから,
\begin{align}I\left(\frac{\sqrt{3}}{4}\right)\leqq I\leqq I\left(\frac{1}{2}\right)\end{align}
\begin{align}\Leftrightarrow \frac{5+4\sqrt{3}}{96}\leqq I\leqq \frac{1}{8}.\end{align}







コメント