問題文全文
座標平面において, 2 つの曲線
\begin{align}y=-x^2+2x+1~~\cdots ①\end{align}
\begin{align}y=-x^2+6x-4~~\cdots ②\end{align}
と 4 点 \(\mathrm{A}(0,~5)\), \(\mathrm{B}(0,~-2)\), \(\mathrm{C}(4,~-2)\), \(\mathrm{D}(4,~5)\) がある. 2 つの曲線 ① と ② の交点を \(\mathrm{E}\) とする.
(1) 交点 \(\mathrm{E}\) の座標は \(\mathrm{E}\left(\fbox{$\hskip0.8em(a)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)\) である.
(2) 2 つの曲線 ① と ② の共通接線の方程式を \(y=px+q\) とするとき, \(p\) と \(q\) の値は \((p,~q)=\left(\fbox{$\hskip0.8em(b)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)\) となる. この接線と曲線 ① との接点を \(\mathrm{F}\), この接線と曲線 ② との接点を \(\mathrm{G}\) とするとき, その座標は \(\mathrm{F}\left(\fbox{$\hskip0.8em(c)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right),~\mathrm{G}\left(\fbox{$\hskip0.8em(d)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)\) である. また, この接線と直線 \(\mathrm{AD}\) との交点を \(\mathrm{H}\) とするとき, その座標は \(\mathrm{H}\left(\fbox{$\hskip0.8em(e)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)\) である.
\((a)\) 〜 \((e)\) の解答群
\begin{align}(00)~\frac{1}{5},~\frac{5}{16}~~~~(01)~\frac{1}{4},~\frac{13}{16}~~~~(02)~\frac{2}{3},~\frac{17}{16}~~~~(03)~\frac{3}{4},~\frac{21}{16}~~~~(04)~\frac{5}{4},~\frac{23}{16}\end{align}
\begin{align}(05)~\frac{3}{2},~\frac{29}{16}~~~~(06)~\frac{4}{3},~\frac{31}{16}~~~~(07)~\frac{9}{4},~\frac{71}{16}~~~~(08)~\frac{1}{5},~\frac{13}{16}~~~~(09)~\frac{1}{4},~\frac{23}{16}\end{align}
\begin{align}(10)~\frac{2}{3},~\frac{21}{16}~~~~(11)~\frac{3}{4},~\frac{271}{16}~~~~(12)~\frac{9}{4},~\frac{5}{16}~~~~(13)~\frac{3}{2},~\frac{17}{16}~~~~(14)~\frac{4}{3},~\frac{23}{16}\end{align}
\begin{align}(15)~\frac{5}{4},~\frac{31}{16}~~~~(16)~\frac{1}{5},~\frac{21}{16}~~~~(17)~\frac{1}{4},~\frac{31}{16}~~~~(18)~\frac{2}{3},~\frac{29}{16}~~~~(19)~\frac{9}{4},~\frac{23}{16}\end{align}
\begin{align}(20)~\frac{21}{8},~3~~~~(21)~\frac{23}{8},~4~~~~(22)~\frac{29}{8},~5~~~~(23)~\frac{31}{8},~6~~~~(24)~\frac{21}{8},~5\end{align}
\begin{align}(25)~\frac{23}{8},~6~~~~(26)~\frac{29}{8},~3~~~~(27)~\frac{31}{8},~5~~~~(28)~\frac{23}{8},~3~~~~(29)~その他\end{align}
(3) 線分 \(\mathrm{AB}\), 線分 \(\mathrm{AD}\) および (2) で求めた共通接線 \(y=px+q\) で囲まれる図形の面積は \(\fbox{$\hskip0.8em(f)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である. また, 線分 \(\mathrm{AB}\), 線分 \(\mathrm{BC}\), 曲線 ① および直線 \(x=t\) で囲まれる図形の面積は \(\fbox{$\hskip0.8em(g)\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) である. ここで, \(t\) は交点 \(\mathrm{E}\) の \(x\) 座標である.
\((f)\) と \((g)\) の解答群
\begin{align}(00)~\frac{1311}{256}~~~~(01)~\frac{1317}{256}~~~~(02)~\frac{1319}{256}~~~~(03)~\frac{1321}{256}~~~~(04)~\frac{1323}{256}\end{align}
\begin{align}(05)~\frac{1327}{256}~~~~(06)~\frac{1349}{256}~~~~(07)~\frac{1359}{256}~~~~(08)~\frac{1361}{256}~~~~(09)~\frac{1367}{256}\end{align}
\begin{align}(10)~\frac{869}{192}~~~~(11)~\frac{871}{192}~~~~(12)~\frac{875}{192}~~~~(13)~\frac{877}{192}~~~~(14)~\frac{881}{192}\end{align}
\begin{align}(15)~\frac{883}{192}~~~~(16)~\frac{891}{192}~~~~(17)~\frac{893}{192}~~~~(18)~\frac{895}{192}~~~~(19)~その他\end{align}

quandle
何だか沢山の選択肢があります. これだけ細かいとピッタリ解答が合わないと正解にはならなそうです. すべて教科書レベルですので着眼点はありません. ミスなく計算するのみです.
(1) の解答
\begin{align}-x^2+2x+1=-x^2+6x-4\end{align}
を解くと,
\begin{align}x=\frac{5}{4}\end{align}
このとき,
\begin{align}y=-\left(\frac{5}{4}\right)^2+2\cdot \frac{5}{4}+1=\frac{-25+40+16}{16}=\frac{31}{16}\end{align}
であるから,
\begin{align}\mathrm{E}\left(\frac{5}{4},~\frac{31}{16}\right).~~~~\cdots(15)\end{align}
(2) の解答
\begin{align}-x^2+2x+1=px+q\end{align}
つまり
\begin{align}x^2+(p-2)x+q-1=0~~~~\cdots ③\end{align}
の判別式を \(D_1\) とおくと, \(D_1=0\) より,
\begin{align}D_1=(p-2)^2-4(q-1)=0\end{align}
\begin{align}q=\frac{(p-2)^2}{4}+1\end{align}
\begin{align}-x^2+6x-4=px+q\end{align}
つまり
\begin{align}x^2+(p-6)x+q+4=0~~~~\cdots ④\end{align}
の判別式を \(D_2\) とおくと, \(D_2=0\) より,
\begin{align}D_2=(p-6)^2-4(q+4)=0\end{align}
\begin{align}q=\frac{(p-6)^2}{4}-4\end{align}
よって,
\begin{align}\frac{(p-2)^2}{4}+1=\frac{(p-6)^2}{4}-4\end{align}
\begin{align}\Leftrightarrow (p-2)^2-(p-6)^2+20=0\end{align}
これを解いて,
\begin{align}p=\frac{3}{2}\end{align}
このとき,
\begin{align}q=\frac{1}{4}\cdot \left(\frac{3}{2}-2\right)^2+1=\frac{17}{16}\end{align}
であるから,
\begin{align}(p,~q)=\left(\frac{3}{2},~\frac{17}{16}\right).~~~~\cdots (13)\end{align}
③ に \(\displaystyle (p,~q)=\left(\frac{3}{2},~\frac{17}{16}\right)\) を代入して,
\begin{align}x^2-\frac{1}{2}x+\frac{1}{16}=0\Leftrightarrow \left(x-\frac{1}{4}\right)^2=0\end{align}
\begin{align}x=\frac{1}{4}\end{align}
このとき,
\begin{align}y=\frac{3}{2}\cdot \frac{1}{4}+\frac{17}{16}=\frac{23}{16}\end{align}
であるから,
\begin{align}\mathrm{F}\left(\frac{1}{4},~\frac{23}{16}\right)~~~~\cdots (09).\end{align}
④ に \(\displaystyle (p,~q)=\left(\frac{3}{2},~\frac{17}{16}\right)\) を代入して,
\begin{align}x^2-\frac{9}{2}x+\frac{81}{16}=0\Leftrightarrow \left(x-\frac{9}{4}\right)^2=0\end{align}
\begin{align}x=\frac{9}{4}\end{align}
このとき,
\begin{align}y=\frac{3}{2}\cdot \frac{9}{4}+\frac{17}{16}=\frac{71}{16}\end{align}
であるから,
\begin{align}\mathrm{G}\left(\frac{9}{4},~\frac{71}{16}\right).~~~~\cdots (07)\end{align}
(3) の解答
\(\mathrm{A}(0,~5),~\mathrm{D}(4,~5)\) より, \(y\) 座標が一致しているから, 直線 \(\mathrm{AD}~:~y=5\) である.
共通接線 \(\displaystyle y=\frac{3}{2}x+\frac{17}{16}\) と直線 \(\mathrm{AD}~:~y=5\) との交点の \(x\) 座標は,
\begin{align}\frac{3}{2}x+\frac{17}{16}=5\end{align}
を解いて,
\begin{align}x=\frac{21}{8}\end{align}
となる. よって,
\begin{align}\mathrm{H}\left(\frac{21}{8},~5\right).~~~~\cdots (24)\end{align}
線分 \(\mathrm{AB}\) と線分 \(\mathrm{AD}\) と共通接線 \(\displaystyle y=\frac{3}{2}x+\frac{17}{16}\) で囲まれる図形は下図の青色部分である.
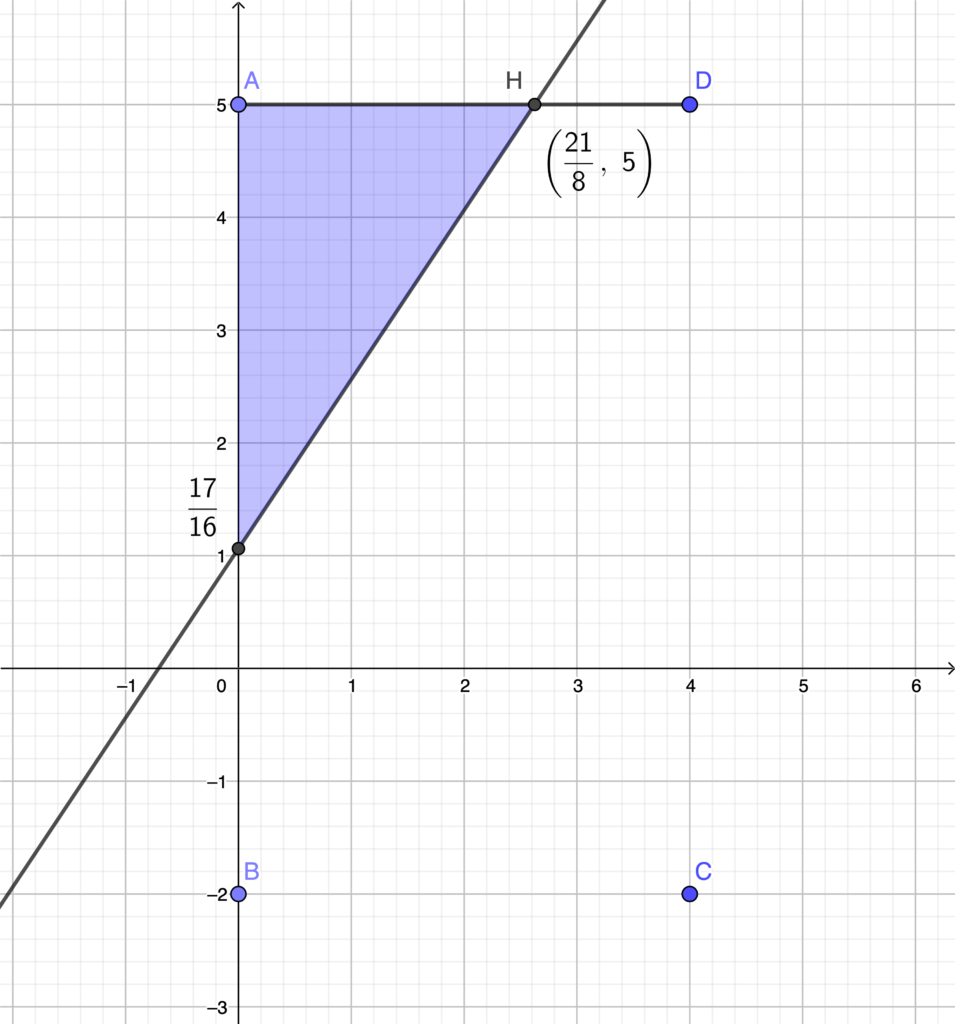
よって, 求める面積は,
\begin{align}\frac{1}{2}\cdot \left(5-\frac{17}{16}\right)\cdot \frac{21}{8}=\frac{1}{2}\cdot \frac{63}{16}\cdot \frac{21}{8}=\frac{1323}{256}~~~~\cdots (04)\end{align}
また, 線分 \(\mathrm{AB}\), 線分 \(\mathrm{BC}\), 曲線 ①, 直線 \(\displaystyle y=\frac{5}{4}\) で囲まれる図形は, 下図の青色部分である.
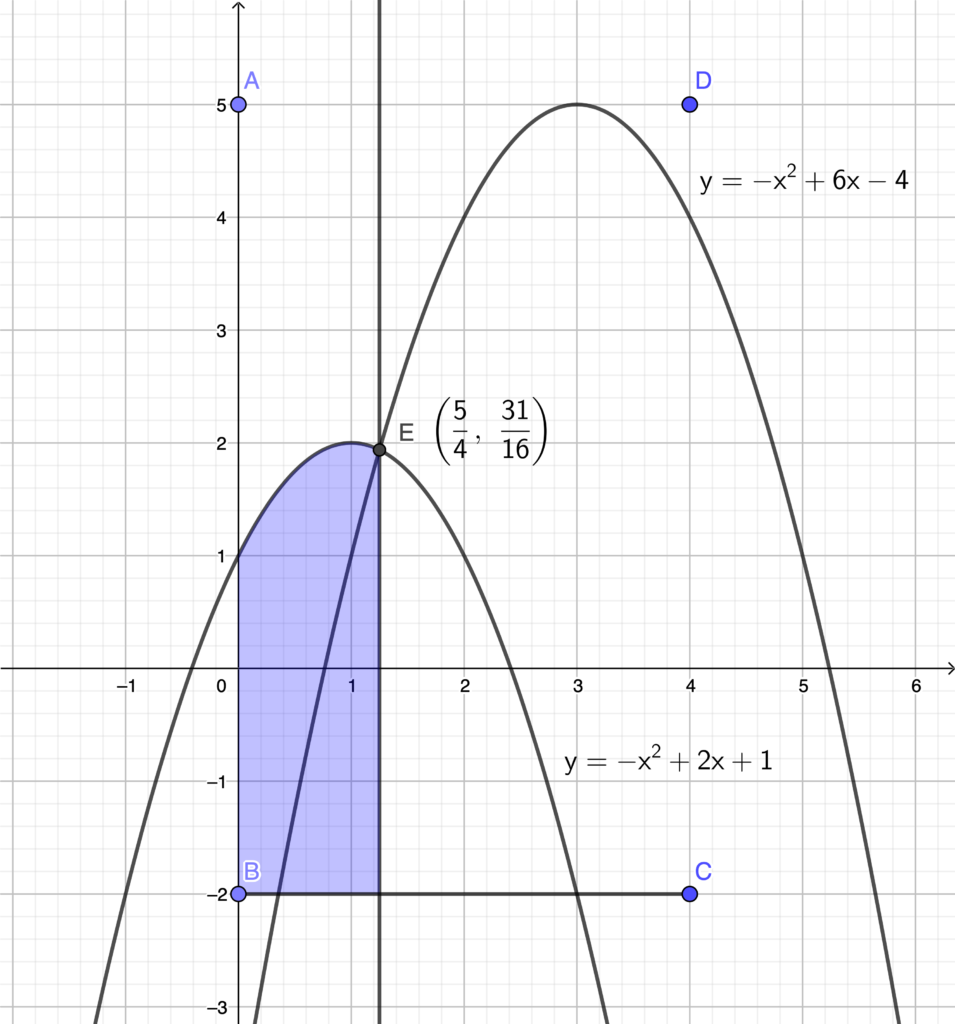
よって, 求める面積は,
\begin{align}\int_0^{\frac{5}{4}}\{-x^2+2x+1-(-2)\}dx=\int_0^{\frac{5}{4}}(-x^2+2x+3\)dx\end{align}
\begin{align}=\biggl[-\frac{1}{3}x^3+x^2+3x\biggr]_0^{\frac{5}{4}}=-\frac{1}{3}\cdot \frac{125}{64}+\frac{25}{16}+\frac{15}{4}\end{align}
\begin{align}=\frac{-125+300+720}{192}=\frac{895}{192}.~~~~\cdots (18)\end{align}







コメント