問題文全文
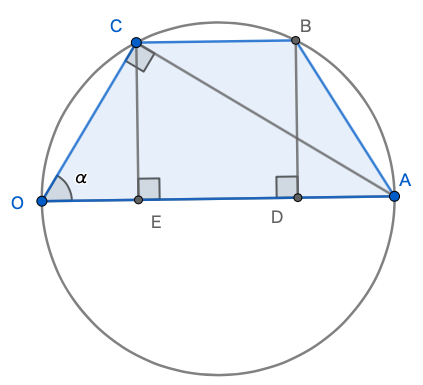
台形 \(\mathrm{OABC}\) が\(,\) 辺 \(\mathrm{OA}\) を直径とする円に内接している. \(\mathrm{OA}\) の長さを 2\(,\) 台形の内角 \(\angle \mathrm{AOC}=\alpha\) とするとき\(,\) 以下の問いに答えなさい.
(1) 辺 \(\mathrm{OC}\) および \(\mathrm{BC}\) の長さを \(\alpha\) を用いて表すと\(,\)
\(\mathrm{OC}=\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos{\alpha},~\mathrm{BC}=\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}-\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos^2{\alpha}\) である.
(2) \(\alpha\) のとり得る値の範囲は \(\displaystyle \frac{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi <\alpha <\frac{\fbox{$\hskip0.8emカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\) である. \(\alpha\) がこの範囲を動くとき\(,\) 台形 \(\mathrm{OABC}\) の面積は \(\displaystyle \alpha =\frac{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\) で最大値 \(\displaystyle \frac{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) をとる.
(3) 座標平面において点 \(\mathrm{O}\) を原点に\(,\) 点 \(\mathrm{A}\) を \((2,~0)\) にとる. \(\mathrm{OP}+\mathrm{AP}=\mathrm{OC}+\mathrm{AC}\) を満たす動点 \(\mathrm{P}(x,~y)\) の軌跡を表す方程式は
\begin{align}\frac{\left(x-\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)^2}{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}+\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos{\alpha}\sin{\alpha}}+\frac{y^2}{\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos{\alpha}\sin{\alpha}}=1\end{align}
である.
(1) の着眼点
円に台形が内接しています. 円に内接する台形は必ず等脚台形になるので\(,\) 注目しておきましょう.
また \(\mathrm{OA}\) は直径です. 直径が与えられたら円周角が直角であることに注目しましょう.
(1) の解答
上図のように等脚台形になる. \(\mathrm{OA}\) が直径であることから\(\displaystyle ,~\angle \mathrm{OCA}=\frac{\pi}{2}\) である.
よって\(,~\triangle \mathrm{OAC}\) に注目して\(,~\mathrm{OC}=2\cos{\alpha}.\)
\(\mathrm{B,~C}\) から \(\mathrm{OA}\) に下ろした垂線の足をそれぞれ \(\mathrm{D,~E}\) とおく.
等脚台形であることから\(,\) \(\mathrm{OE}=\mathrm{AD}(=2\cos^2{\alpha})\) なので\(,\)
\begin{align}\mathrm{BC}=\mathrm{DE}=\mathrm{OA}-\mathrm{OE}-\mathrm{AD}\end{align}
\begin{align}=2-2\cdot 2\cos^2{\alpha}=2-4\cos^2{\alpha}.\end{align}
(2) の解答
\(\mathrm{OC}>0\) より\(,~2\cos{\alpha}>0\) であるから
\begin{align}0<\alpha <\frac{\pi}{2}~~~~\cdots ①\end{align}
\(\mathrm{BC}>0\) より\(,~2-4\cos^{\alpha}>0\) であるから
\begin{align}-\frac{1}{\sqrt{2}}<\cos{\alpha}<\frac{1}{\sqrt{2}}\end{align}
\begin{align}\frac{\pi}{4}<\alpha <\frac{3}{4}\pi~~~~\cdots ②\end{align}
①\(,\) ②より
\begin{align}\frac{\pi}{4}<\alpha <\frac{\pi}{2}.\end{align}
台形 \(\displaystyle \mathrm{OABC}=\frac{1}{2}\cdot (\mathrm{OA}+\mathrm{BC})\cdot \mathrm{CE}\)
\begin{align}=\frac{1}{2}\{2+(2-4\cos^2{\alpha})\}\cdot 2\cos{\alpha}\sin{\alpha}=2\sin^3{\alpha}\cos{\alpha}\end{align}
\(f(\alpha)=2\sin^3{\alpha}\cos{\alpha}\) とおく.
\begin{align}f^{\prime}(\alpha)=6\sin^2{\alpha}\cos^2{\alpha}-2\sin^4{\alpha}\end{align}
\begin{align}=2\sin^2{\alpha}(3\cos^2{\alpha}-\sin^2{\alpha})=2\sin^2{\alpha}(3-4\sin^2{\alpha})\end{align}
\begin{align}=2\sin^2{\alpha}(\sqrt{3}-2\sin{\alpha})(\sqrt{3}+2\sin{\alpha})\end{align}
\(\displaystyle \frac{\pi}{4}<\alpha <\frac{\pi}{2}\) より\(,\)
\begin{align}2\sin^2{\alpha}(\sqrt{3}+2\sin{\alpha})>0\end{align}
であるから\(,\) \(f^{\prime}(\alpha)\) の符号は \(\sqrt{3}-2\sin{\alpha}\) の符号によって決まる.
これを踏まえると\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{c|c|c|c|c|c|}\alpha & \displaystyle \frac{\pi}{4} & \cdots & \displaystyle \frac{\pi}{3} & \cdots & \displaystyle \frac{\pi}{2} \\ \hline f^{\prime}(\alpha) & {} & + & 0 & – & {} \\ \hline f(\alpha) & \displaystyle \left(\frac{1}{2}\right) & \nearrow & 最大 & \searrow & (0) \\ \end{array}\end{align}
増減表より\(,\) \(\displaystyle \alpha =\frac{\pi}{3}\) のとき\(,\) 最大値
\begin{align}f\left(\frac{\pi}{3}\right)=2\cdot \left(\frac{\sqrt{3}}{2}\right)^3\cdot \frac{1}{2}=\frac{3}{8}\sqrt{3}.\end{align}
(3) の着眼点
求める \(\mathrm{P}\) の軌跡は
\begin{align}\frac{\left(x-\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)^2}{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}+\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos{\alpha}\sin{\alpha}}+\frac{y^2}{\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos{\alpha}\sin{\alpha}}=1\end{align}
という形になることが分かっています.
\begin{align}a=\sqrt{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}+\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos{\alpha}\sin{\alpha}},~b=\sqrt{\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\cos{\alpha}\sin{\alpha}}\end{align}
とおいてみると\(,\)
\begin{align}\frac{\left(x-\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)^2}{a^2}+\frac{y^2}{b^2}=1\end{align}
ですから\(,\) 楕円になることが予想できます.
ここで\(,\) 楕円の定義を思い出してみると「2 定点からの距離の和が一定である点の軌跡」でした. この視点を持って与えられた
\begin{align}\mathrm{OP}+\mathrm{AP}=\mathrm{OC}+\mathrm{AC}\end{align}
の式を眺めてみると\(,\) 点 \(\mathrm{C}\) は定点ですから\(,\) \(\mathrm{OC}+\mathrm{AC}\) は定数です.
このことから\(,\) 点 \(\mathrm{O}\) と点 \(\mathrm{A}\) を 2 焦点とする楕円になるのではないかという予想ができます.
(3) の解答
\(\triangle \mathrm{OAC}\) に注目すると\(,\)
\begin{align}\mathrm{OC}=2\cos{\alpha},~\mathrm{AC}=2\sin{\alpha}\end{align}
となるので\(,\)
\begin{align}\mathrm{OC}+\mathrm{AC}=2(\sin{\alpha}+\cos{\alpha})=(一定)\end{align}
となる. 条件より\(,\)
\begin{align}\mathrm{OP}+\mathrm{AP}=\mathrm{OC}+\mathrm{AC}=(一定)\end{align}
となるから\(,\) 求める \(\mathrm{P}\) の軌跡は 2 点 \(\mathrm{O,~A}\) を焦点とする楕円となる.
※ \(\mathrm{P}\) をつまんで動かしてみてください. 楕円が描かれます.
正の数 \(b\) を用いて楕円の方程式を求めると
\begin{align}\frac{(x-1)^2}{(\cos{\alpha}+\sin{\alpha})^2}+\frac{y^2}{b^2}=1\end{align}
\begin{align}\Leftrightarrow \frac{(x-1)^2}{1+2\cos{\alpha}\sin{\alpha}}+\frac{y^2}{b^2}=1\end{align}
楕円の中心から焦点までの距離は \(\mathrm{OA}\) の長さの半分 1 に等しいので\(,\)
\begin{align}(1+2\cos{\alpha}\sin{\alpha})-b^2=1\end{align}
\begin{align}b^2=2\cos{\alpha}\sin{\alpha}\end{align}
したがって
\begin{align}\frac{(x-1)^2}{1+2\cos{\alpha}\sin{\alpha}}+\frac{y^2}{2\cos{\alpha}\sin{\alpha}}=1.\end{align}




コメント