問題文全文
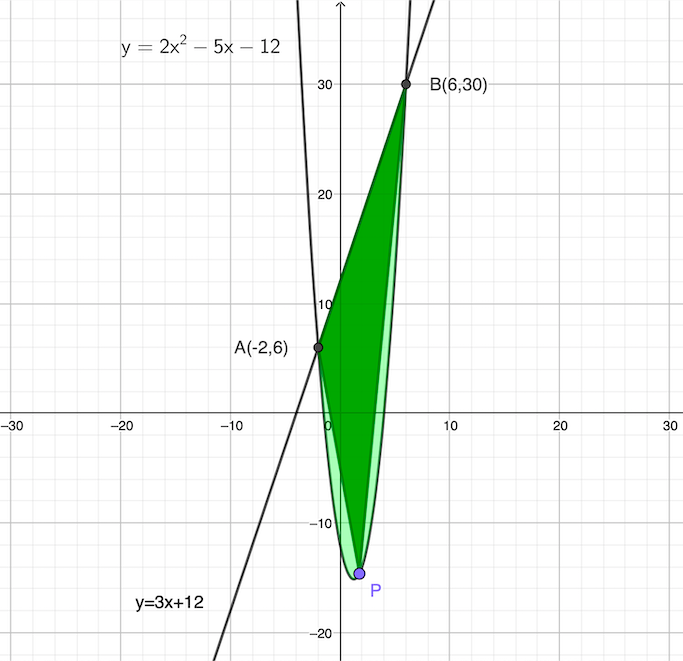
放物線 \(y=2x^2-5x-12\) と直線 \(y=3x+12\) がある. いま\(,\) 点 \(\mathrm{P}\) が放物線上を動くとする. このとき\(,\) 次の各問いに答えなさい.
(1) 点 \(\mathrm{P}\) が直線 \(y=3x+12\) 上にないとする. 点 \(\mathrm{P}\) の \(x\) 座標を \(t\) とするとき\(,\) 放物線 \(y=2x^2-5x-12\) と直線 \(y=3x+12\) の 2 つの交点と点 \(\mathrm{P}\) を結ぶ三角形の面積 \(S\) を求めなさい.
(2) (1) の面積 \(S\) が\(,\) 放物線 \(y=2x^2-5x-12\) と直線 \(y=3x+12\) で囲まれた面積の\(\displaystyle \frac{3}{4}\) となるとき\(,\) \(t\) の値を求めなさい.
(1) の解答
\begin{align}2x^2-5x-12=3x+12\end{align}
\begin{align}2x^2-8x-24=0\end{align}
\begin{align}x^2-4x-12=0\end{align}
\begin{align}(x-6)(x+2)=0\end{align}
\begin{align}x=-2,~6\end{align}
交点を \(\mathrm{A}(-2,~6),~\mathrm{B}(6,~30)\) とおく. また\(,\) 点 \(\mathrm{P}\) から直線 \(\mathrm{AB}\) に下ろした垂線の足を \(\mathrm{H}\) とおく.
点 \(\mathrm{P}(t,~2t^2-5t-12)\) と直線 \(3x-y+12=0\) との距離 \(\mathrm{PH}\) は
\begin{align}\mathrm{PH}=\frac{|3t-(2t^2-5t-12)+12|}{\sqrt{3^2+(-1)^2}}=\frac{|2t^2-8t-24|}{\sqrt{10}}\end{align}
\(\mathrm{A}(-2,~6),~\mathrm{B}(6,~30)\) より
\begin{align}\mathrm{AB}=\sqrt{\{6-(-2)\}^2+(30-6)^2}=8\sqrt{10}\end{align}
よって\(,\)
\begin{align}S=\frac{1}{2}\cdot 8\sqrt{10}\cdot \frac{|2t^2-8t-24|}{\sqrt{10}}\end{align}
\begin{align}S=8|t^2-4t-12|.\end{align}
(2) の解答
放物線と直線で囲まれた部分の面積を \(T\) とおくと
\begin{align}T=\int_{-2}^6\{3x+12-(2x^2-5x-12)\}dx\end{align}
\begin{align}=-2\int_{-2}^{6}(x+2)(x-6)dx=\frac{2}{6}\{6-(-2)\}^3=\frac{512}{3}\end{align}

quandle
「放物線と直線で囲まれた部分の面積」と言われたら\(\displaystyle \frac{1}{6}\) 公式の出番です!
\(\displaystyle S=\frac{3}{4}T\) より
\begin{align}8|t^2-4t-12|=\frac{3}{4}\cdot \frac{512}{3}\end{align}
\begin{align}|t^2-4t-12|=16\end{align}
\begin{align}t^2-4t-28=0~or~t^2-4t+4=0\end{align}
\begin{align}t=2\pm 4\sqrt{2} ,~ 2.\end{align}






コメント