C方式・グローバル方式2022年第4問の問題文全文
以下の定積分の値を求めよ. ただし\(,\) \(e\) は自然対数の底で\(,\) \(\log{}\) は自然対数を表す.
(1) \(\displaystyle \int_1^4\sqrt{(4-x)(x-1)}dx=\frac{~\fbox{$\hskip0.4emモ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emヤ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\pi\)
(2) \(\displaystyle \int_1^e\log{\left(\sqrt{x}\right)}dx=\frac{~\fbox{$\hskip0.4emユ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emヨ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\)
(3) \(\displaystyle \int_0^4\frac{2}{(x+1)(x+2)(x+3)}dx=\log{\frac{~\fbox{$\hskip0.4emラリ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emルレ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}}\)
(1) の着眼点〜\(\sqrt{a^2-x^2}\) の積分は \(x=a\sin{\theta}\) とおく〜
無理関数を含む積分は難しいです. 基本的には置換積分になりますが\(,\) 与えられた形に合わせて色々な置換が考えられるため\(,\) 分岐が多いためです.
今回の問題は平方完成を行うことで \(\sqrt{a^2-x^2}\) の積分に帰着できます.
\(\sqrt{a^2-x^2}\) の積分は \(x=a\sin{\theta}\) と置換することでうまくいきます.
(1) の解答〜平方完成して\(\sqrt{a^2-x^2}\) の形を作る〜
\begin{align}I=\int_1^4\sqrt{(4-x)(x-1)}dx=\int_1^4\sqrt{-x^2+5x-4}dx\end{align}
\begin{align}=\int_1^4\sqrt{-\left(x-\frac{5}{2}\right)^2+\frac{9}{4}}dx\end{align}
\(\displaystyle x-\frac{5}{2}=\frac{3}{2}\sin{\theta}\) とおくと\(,\)
\begin{align}dx=\frac{3}{2}\cos{\theta}d\theta\end{align}
\begin{align}\begin{array}{|c|ccc|}\hline x & 1 & \to & 4 \\ \hline \theta & \displaystyle -\frac{\pi}{2} & \to & \displaystyle \frac{\pi}{2} \\ \hline \end{array}\end{align}
\begin{align}I=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{\frac{9}{4}(1-\sin^2{\theta})}\cdot \frac{3}{2}\cos{\theta}d\theta \end{align}
\begin{align}=\frac{9}{4}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{\cos^2{\theta}}\cdot \cos{\theta}d\theta=\frac{9}{4}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^2{\theta}d\theta\end{align}

quandle
本来は \(\sqrt{\cos^2{\theta}}=|\cos{\theta}|\) と絶対値がつきます. 今回は 積分範囲が\(\displaystyle -\frac{\pi}{2}\leqq \theta \leqq \frac{\pi}{2}\) ですから常に \(\cos{\theta}\geqq 0\) となるため絶対値をはずしています.
\begin{align}=\frac{9}{4}\cdot 2\int_0^{\frac{\pi}{2}}\frac{1+\cos{2\theta}}{2}d\theta\end{align}

quandle
\(\cos^2{\theta}\) は偶関数です. 一般に \(f(x)\) が偶関数のとき
\begin{align}\int_{-a}^af(x)dx=2\int_0^af(x)dx\end{align}
となるのでしたね.
また\(,\) \(\cos^2{\theta}\) は半角の公式を使うことで次数を下げます.
\begin{align}=\frac{9}{4}\biggl[\theta +\frac{1}{2}\sin{2\theta}\biggr]_0^{\frac{\pi}{2}}=\frac{9}{8}\pi~~~~\cdots \fbox{答}\end{align}
別解〜半円の面積と見る〜
被積分関数を\(y\) とおいてグラフをかいてみます.
\(\displaystyle y=\sqrt{-\left(x-\frac{5}{2}\right)^2+\frac{9}{4}}\) とおくと\(,\) \(y\geqq 0\)であり\(,\)
\begin{align}\left(x-\frac{5}{2}\right)^2+y^2=\frac{9}{4}\end{align}
であるから\(,\) 求める積分の値は下図の面積と一致する.
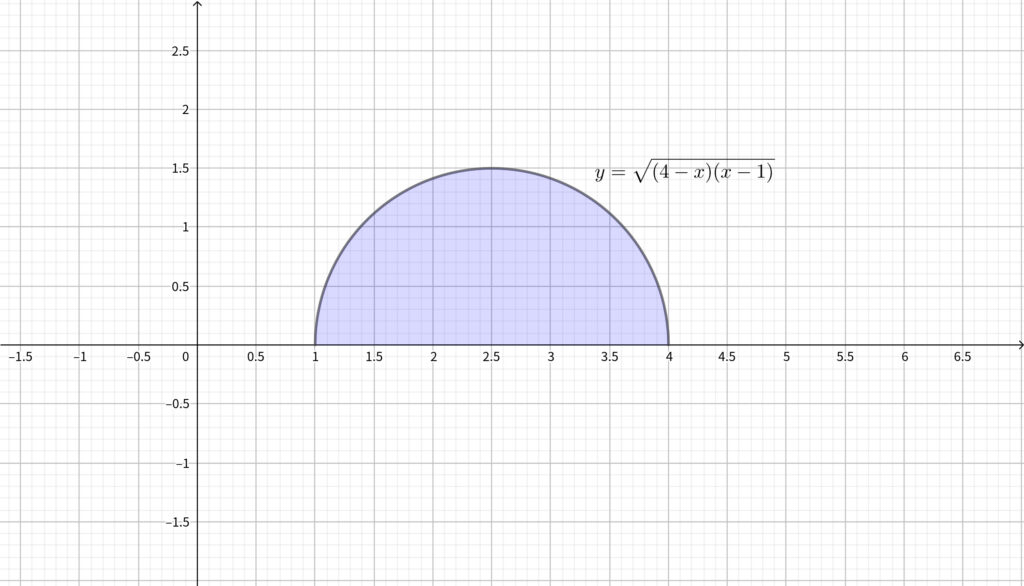
上の図は中心 \(\displaystyle \left(\frac{5}{2},~0\right)\) 半径 \(\displaystyle \frac{3}{2}\) の円の上半分であるから\(,\) その面積は
\begin{align}\frac{1}{2}\cdot \left(\frac{3}{2}\right)^2\pi=\frac{9}{8}\pi ~~~~\cdots \fbox{答}\end{align}
モ:9 ヤ:8
(2) の解答〜\(\log{x}\) の積分は覚えておく〜
\begin{align}\int_1^e\log{\left(\sqrt{x}\right)}dx=\frac{1}{2}\int_1^e\log{x}dx\end{align}
\begin{align}=\frac{1}{2}\biggl[x\log{x}-x\biggr]_1^e=\frac{1}{2}(e-e+1)=\frac{1}{2}~~~~\cdots \fbox{答}\end{align}

quandle
\begin{align}\int \log{x}dx=x\log{x}-x+C\end{align}
はよく出るので結果を暗記しておきましょう. 当然忘れたときのために導出もできることが前提ですよ. (\(\log{x}=1\cdot \log{x}\) とみて部分積分でしたね.)
ユ:1 ヨ:2
(3) の解答〜部分分数分解の利用〜
\begin{align}\int_0^4\frac{2}{(x+1)(x+2)(x+3)}dx=\int_0^4\left(\frac{1}{x+1}-\frac{2}{x+2}+\frac{1}{x+3}\right)dx\end{align}
\begin{align}=\biggl[\log{|x+1|}-2\log{|x+2|}+\log{|x+3|}\biggr]_0^4=\biggl[\log{\frac{(x+1)(x+3)}{(x+2)^2}}\biggr]_0^4\end{align}

quandle
\(0\leqq x\leqq 4\) の範囲において考えればいいので絶対値は外しています.
\begin{align}\log{\frac{35}{36}}-\log{\frac{3}{4}}=\log{\frac{35}{27}}~~~~\cdots \fbox{答}\end{align}
ラ:3 リ:5 ル:2 レ:7
補足:\(\displaystyle \frac{2}{(x+1)(x+2)(x+3)}\) の部分分数分解
\begin{align}\frac{2}{(x+1)(x+2)(x+3)}=\frac{a}{x+1}+\frac{b}{x+2}+\frac{c}{x+3}\end{align}
となる実数 \(a,~b,~c\) がわかれば部分分数分解できます. \(x\) に関する恒等式と見ることで計算ができます.
両辺に \((x+1)(x+2)(x+3)\) をかけると\(,\)
\begin{align}a(x+2)(x+3)+b(x+1)(x+3)+c(x+1)(x+2)=2\end{align}
\begin{align}(a+b+c)x^2+(5a+4b+3c)x+6a+3b+2c=2\end{align}
係数を比較すると\(,\)
\begin{align}\left\{\begin{array}{c}a+b+c=0 \\ 5a+4b+3c=0 \\ 6a+3b+2c=2\\ \end{array}\right.\end{align}
これを解いて\(,\) \(a=1,~b=-2,~c=1\) を得る.









コメント