山口東京理科大学工学部中期第１問(3)(5)の問題文全文
(3) \(0\leqq x \leqq 2\pi\) において定義された \(2\) つの関数を
\begin{align}f(x)=x\cos{x},~g(x)=x\end{align}
とする. 曲線 \(y=f(x)\)\(,\) 直線 \(x=2\pi \) と \(x\) 軸で囲まれた部分の面積を \(S_1\)\(,\) 曲線 \(y=f(x)\) と直線 \(y=g(x)\) で囲まれた部分の面積を \(S_2\) とする. このとき\(,\) \(S_1\) および \(S_2\) は
\begin{align}S_1=~\fbox{$\hskip0.4emク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\pi ,~S_2=~\fbox{$\hskip0.4emケ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~{\pi}^{~\fbox{$\hskip0.4emコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である.
(5) 関数 \(f(x)\) は
\begin{align}f(x)=x^2+\int_0^2(3x-2t)f(t)dt\end{align}
を満たす. このとき\(,\) 関数 \(f(x)\) は\(,\)
\begin{align}f(x)=x^2-\frac{~\fbox{$\hskip0.4emソ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emタ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~x-\frac{~\fbox{$\hskip0.4emチ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emツテ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である.
(3) の着眼点〜面積はグラフの上下関係さえわかればよい〜
いきなり \(f(x)\) を微分してグラフを描こうとしていませんか？ 実際にやってみるとわかりますが\(,\) 微分しても \(x\) と三角関数が混在する式が出てきてしまって\(,\) \(f^{\prime}(x)=0\) を解くことができません. そもそもなぜグラフを描く必要があったのでしょうか？それは \(y=f(x)\) と \(y=g(x)\) のグラフの上下関係を把握するためです.
上下関係さえつかめればよいので\(,\) 積分における面積の問題でとても大事な考え方は
必ずしも正確なグラフを描く必要はない
ということです.
\(f(x)=x\cos{x}\) と \(g(x)=x\) のグラフの上下関係
\(0\leqq x\leqq 2\pi \) より\(,\)
\begin{align}-1\leqq \cos{x}\leqq 1\end{align}
なので\(,\) 辺々に \(x~(>0)\) をかけて\(,\)
\begin{align}-x\leqq x\cos{x} \leqq x\end{align}
であるから\(,\) \(0\leqq x \leqq 2\pi \) において\(,\) 常に
\begin{align}f(x)\leqq g(x)\end{align}
であることがわかる.
quandle
\(f(x)=x\cos{x}\) のグラフの概形はまったくわからないままですが\(,\) 「面積を出す」という目的の達成だけであればこれだけの情報があれば十分です.
なお\(,\) 参考までにグラフは以下のようになります. イメージとしては \(y=x\) の直線にあわせて \(\cos{x}\) の波が大きくなっていく感じです.
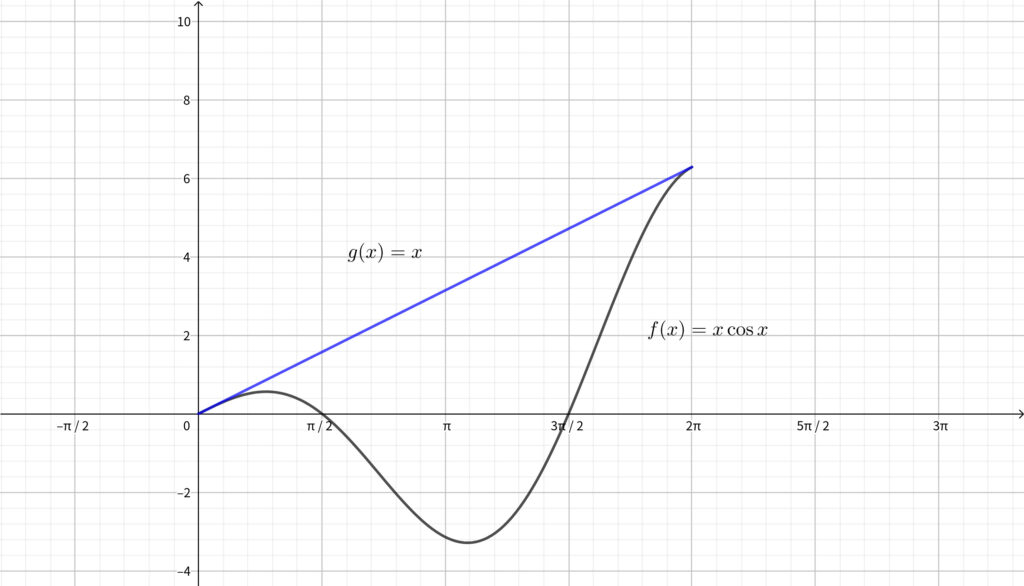常に \(y=x\) の方が上に来ていることがわかる
\(S_1\) を求める〜部分積分の利用〜
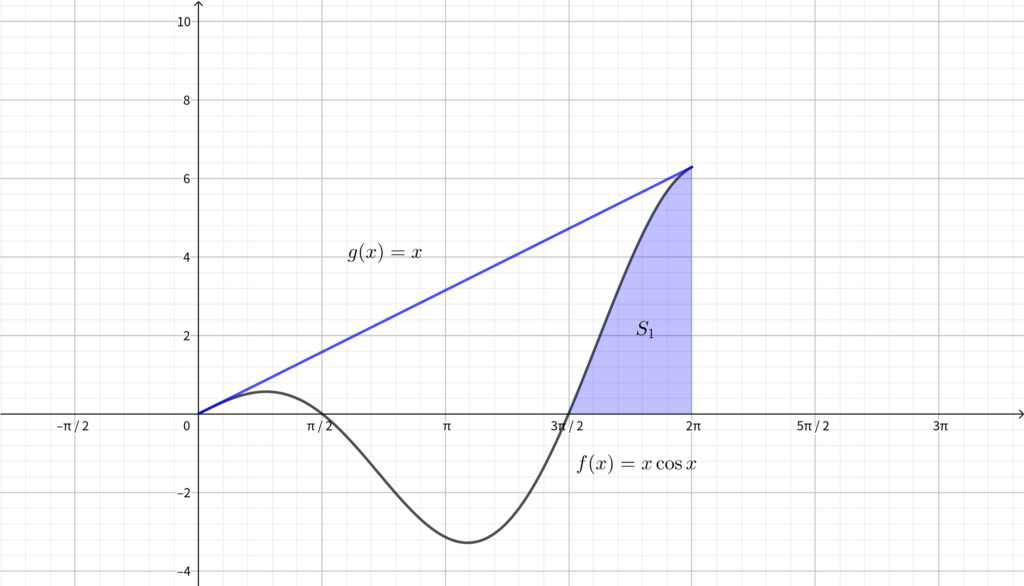図の青色部分の面積を求めればよい
簡単のため \(f(x)\) の原始関数を \(F(x)\) とおいておきます. つまり\(,\)
\begin{align}F(x)=\int x\cos{x}dx=x\sin{x}-\int \cos{x}dx\end{align}
\begin{align}=x\sin{x}+\cos{x}+C\end{align}
となります.
\begin{align}S_1=\int_{\frac{3}{2}\pi}^{2\pi}x\cos{x}dx\end{align}
\begin{align}=\biggl[x\sin{x}+\cos{x}\biggr]_{\frac{3}{2}\pi}^{2\pi}=\biggl[F(x)\biggr]_{\frac{3}{2}\pi}^{2\pi}\end{align}
\begin{align}=\frac{3}{2}\pi +1~~~~\cdots \fbox{答}\end{align}
quandle
答えが出たのに問題文で与えられている形と一致しません.どうやら大学側は \(S_1\) として違う場所を想定していたようです. 今回の問題文であれば筆者としては上図の青色部分と解釈すべきであると考えています.
出題ミスと大学側の対応
大学側は今回の問題文では複数の解釈があるとして\(,\)「 受験生全員を正解とする」という対応を行ったことを公式HPで発表しています.
【工学部】数学 問題：【1】（3）―「ク」 対応 : 受験者全員を正解とする
https://www.socu.ac.jp/entrance/entrance%20exam_HP.pdf
大学側が想定していたこと（予想）
筆者の勝手な予想ではあるのですが\(,\) 恐らく大学側が想定していたのは下図部分だと思います.
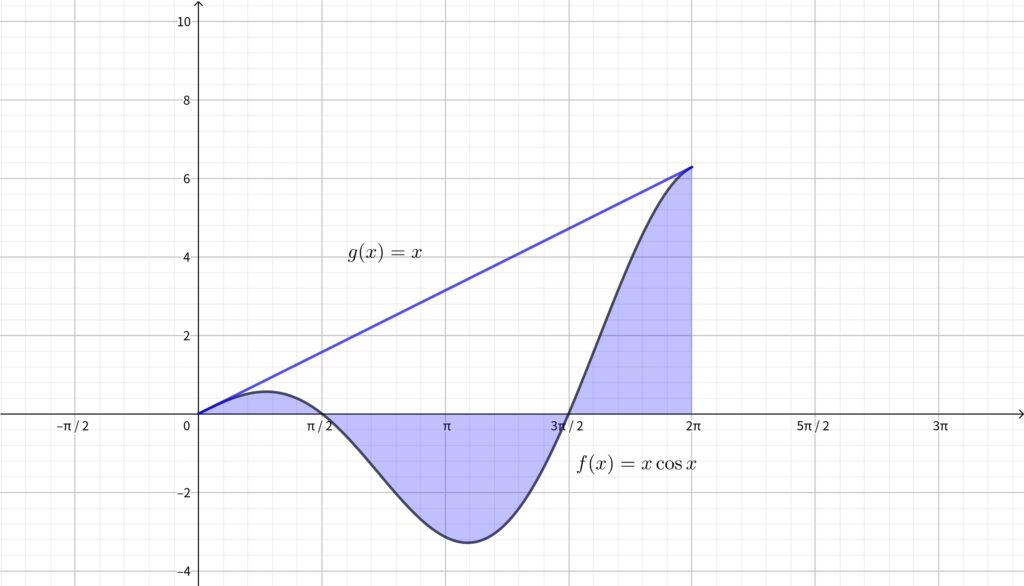
上図の青色部分の面積は
\begin{align}\int_0^{\frac{\pi}{2}}f(x)dx-\int_{\frac{\pi}{2}}^{\frac{3}{2}\pi}f(x)dx+\int_{\frac{3}{2}\pi}^{2\pi}f(x)dx\end{align}
\begin{align}=\biggl[F(x)\biggr]_0^{\frac{\pi}{2}}-\biggl[F(x)\biggr]_{\frac{\pi}{2}}^{\frac{3}{2}\pi}+\biggl[F(x)\biggr]_{\frac{3}{2}\pi}^{2\pi}\end{align}
\begin{align}=-F(0)+2F\left(\frac{\pi}{2}\right)-2F\left(\frac{3}{2}\pi\right)+F(2\pi )\end{align}
\begin{align}=-1+2\cdot \frac{\pi}{2}-2\cdot \left(-\frac{3}{2}\pi\right)+1=4\pi \end{align}
こう解釈すれば問題文で与えられている形とも合致します.
\(S_2\) を求める〜面積は（上の式）ー（下の式）の積分〜
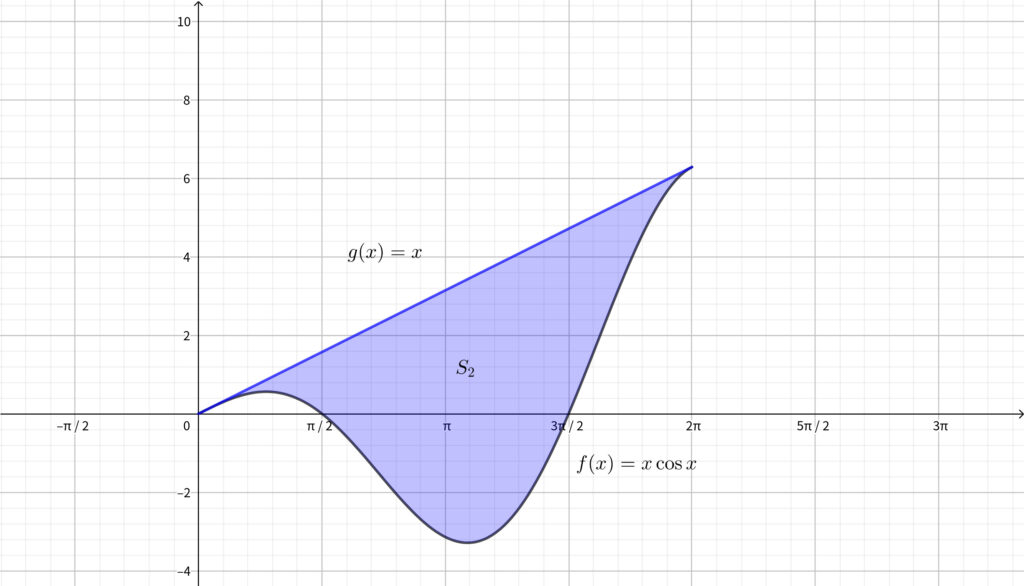青色部分の面積が \(S_2\)
\begin{align}S_2=\int_0^{2\pi}(x-x\cos{x})dx\end{align}
\begin{align}=\biggl[\frac{1}{2}x^2-x\sin{x}-\cos{x}\biggr]_0^{2\pi}\end{align}
\begin{align}=2{\pi}^2-1+1=2{\pi}^2~~~~\cdots \fbox{答}\end{align}
ケ：２ コ：２
(5) の着眼点〜インテグラルの中は \(t\) だけの式に〜
\begin{align}\int_0^2(3x-2t)f(t)dt\end{align}
をどう扱うかで迷う人がいるかもしれません. \(dt\) と書いてありますから当然
「 \(t\) について積分する」
ことになります. 言い換えると
「 \(t\) 以外の文字はすべて定数扱いする」
ということです. まずは \(x\) を定数扱いしてインテグラルの外に出すことから始めましょう！
(5) の解答〜 積分部分は定数とおく〜
\begin{align}f(x)=x^2+\int_0^2(3x-2t)f(t)dt\end{align}
\begin{align}=x^2+3x\int_0^2f(t)dt-2\int_0^2tf(t)dt\end{align}
quandle
\(\displaystyle \int_0^2f(t)dt\) と \(\displaystyle \int_0^2tf(t)dt\) はどちらもインテグラルの中身が \(t\) だけの式なので定数になります. 中身は違う関数ですから一般的には違う定数となります. それぞれを \(a,~b\) とおいて連立方程式を立てましょう！
\begin{align}a=\int_0^2f(t)dt~~\cdots ①,~b=\int_0^2tf(t)dt~~\cdots ②\end{align}
とおく. このとき\(,\) \(f(x)\) は
\begin{align}f(x)=x^2+3ax-2b\end{align}
となる. ① に代入して\(,\)
\begin{align}a=\int_0^2(t^2+3at-2b)dt\end{align}
\begin{align}=\biggl[\frac{1}{3}t^3+\frac{3}{2}at^2-2bt\biggr]_0^2=\frac{8}{3}+6a-4b\end{align}
\begin{align}\therefore ~5a-4b=-\frac{8}{3}~~~~\cdots ③\end{align}
② に代入して\(,\)
\begin{align}b=\int_0^2(t^3+3at^2-2bt)dt\end{align}
\begin{align}=\biggl[\frac{1}{4}t^4+at^3-bt^2\biggr]_0^2=4+8a-4b\end{align}
\begin{align}\therefore ~8a-5b=-4~~~~\cdots ④\end{align}
③\(,\) ④ より\(,\)
\begin{align}a=-\frac{8}{21},~b=\frac{4}{21}\end{align}
\begin{align}\therefore ~f(x)=x^2-\frac{8}{7}x-\frac{8}{21}~~~~\cdots \fbox{答}\end{align}
ソ：８ タ：７ チ：８ ツ：２ テ：１
コメント