経営学部(共通)2024年第1問(2)の問題文全文 関数 \(f(x)\) を
\begin{align}f(x)=\int_1^xt(t-3)dt\end{align}
と定める.
(a) \(x\) が実数全体を動くとき\(,\)
● \(x= \fbox{$\hskip0.4emシ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) のときに \(f(x)\) は極小値
\begin{align}-~\frac{~\fbox{$\hskip0.4emスセ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{\fbox{$\hskip0.4emソ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}\end{align}
をとる.
● \(x= \fbox{$\hskip0.4emタ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) のときに \(f(x)\) は極大値
\begin{align} \frac{~\fbox{$\hskip0.4emチ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emツ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
をとる.
(b) \(\displaystyle s>-\frac{3}{2}\) として\(,\) \(\displaystyle -\frac{3}{2}\leqq x \leqq s\) の範囲を \(x\) が動くとき\(,\)
\begin{align}f\left(-\frac{3}{2}\right)=-~\frac{~\fbox{$\hskip0.4emテト\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{\fbox{$\hskip0.4emナ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}\end{align}
より\(,\) 関数 \(f(x)\) の最大値と最小値の差が \(\displaystyle \frac{9}{2}\) となるような \(s\) の範囲は\(,\)
\begin{align}\fbox{$\hskip0.4emニ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\leqq s \leqq \frac{~\fbox{$\hskip0.4emヌ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emネ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である.
(a) の解答~積分範囲に文字があるときの微分~
\begin{align}f^{\prime}(x)=x(x-3)\end{align}
より\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline x & \cdots & 0 & \cdots & 3 & \cdots \\ \hline f^{\prime}(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\ \hline \end{array}\end{align}
増減表より\(,\) \(x=3\) のとき極小値
\begin{align}f(3)=\int_1^3(t^2-3t)dt\end{align}
\begin{align}=\biggl[\frac{1}{3}t^3-\frac{3}{2}t^2\biggr]_1^3\end{align}
\begin{align}=\frac{1}{3}(27-1)-\frac{3}{2}(9-1)=-\frac{10}{3}~~~~\cdots \fbox{答}\end{align}
\(x=0\) のとき極大値
\begin{align}f(0)=\biggl[\frac{1}{3}t^3-\frac{3}{2}t^2\biggr]_1^0\end{align}
\begin{align}=-\frac{1}{3}+\frac{3}{2}=\frac{7}{6}~~~~\cdots \fbox{答}\end{align}
シ:3 ス:1 セ:0 ソ:3 タ:0 チ:7 ツ:6
(b) の解答 \(\displaystyle f\left(-\frac{3}{2}\right)\) を求める
\begin{align}f\left(-\frac{3}{2}\right)=\biggl[\frac{1}{3}t^3-\frac{3}{2}t^2\biggr]_1^{-\frac{3}{2}}\end{align}
\begin{align}=\frac{1}{3}\left(-\frac{27}{8}-1\right)-\frac{3}{2}\left(\frac{9}{4}-1\right)=-\frac{10}{3}~~~~\cdots \fbox{答}\end{align}
テ:1 ト:0 ナ:3
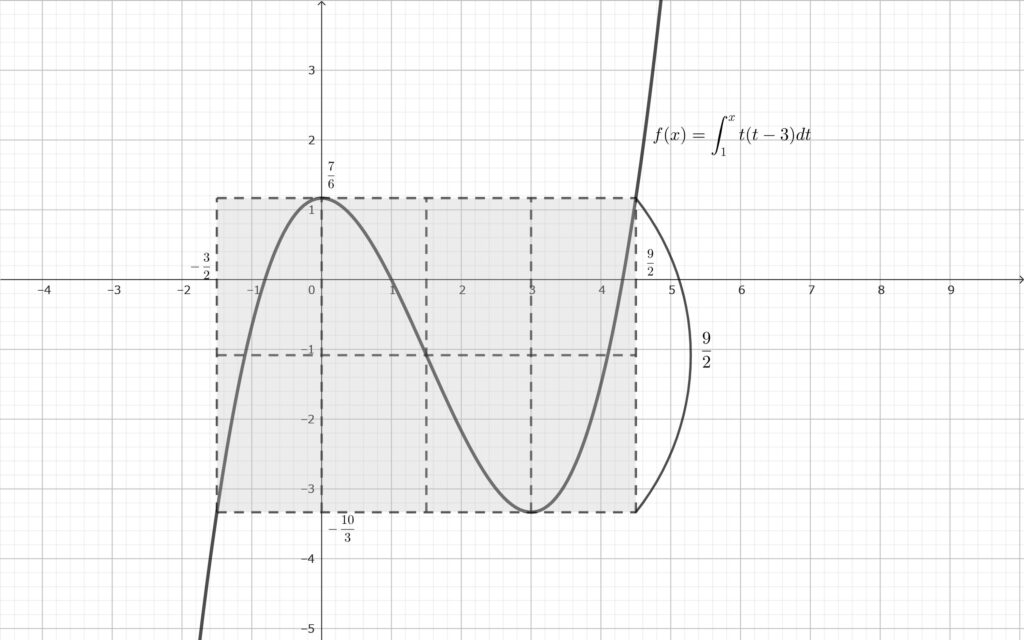
グラフをかいて観察する~4等分の性質を活用~ 3次関数ですから4等分の性質を使って概形をかくことができます. 詳しくは「高校数学の美しい物語」様が証明とともにまとめてらっしゃるので引用させていただきます.
最大値と最小値の差が \(\displaystyle \frac{9}{2}\) とありますがこれはちょうど極大値と極小値の差に一致しています. これに気づければあとは場合分けするだけです. グラフは以下のようになります.
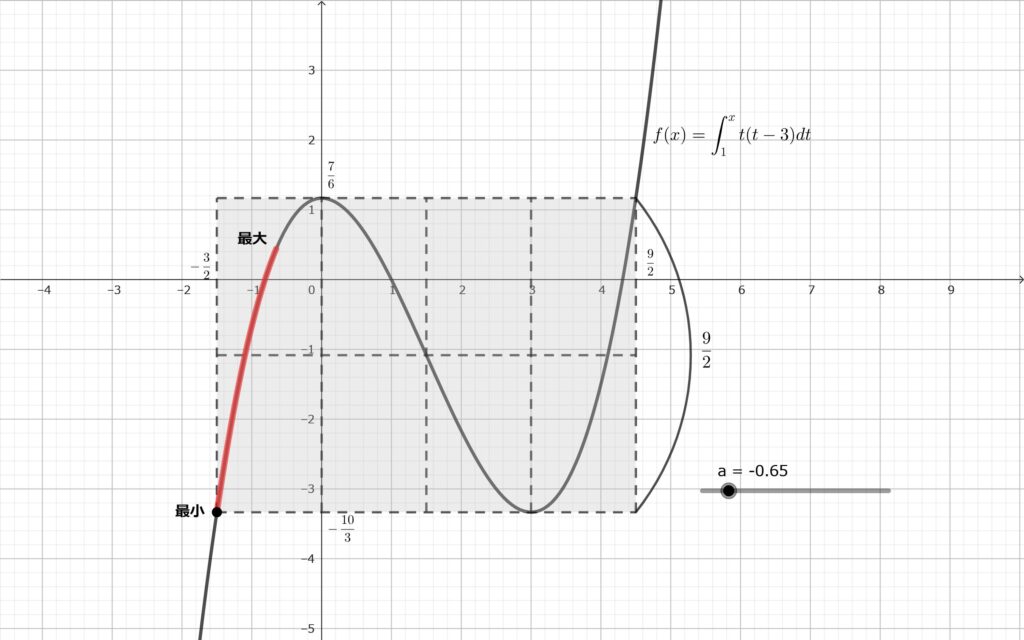
条件を満たす \(s\) の範囲を考える~場合分けする~ \(\displaystyle -\frac{3}{2}<s<0\) のとき\(,\)
\(x=s\) のとき最大値\(,\) \(\displaystyle x=-\frac{3}{2}\) のとき最小値をとるが\(,\) 上図より\(,\) 最大値と最小値の差は \(\displaystyle \frac{9}{2}\) より小さくなるため不適.
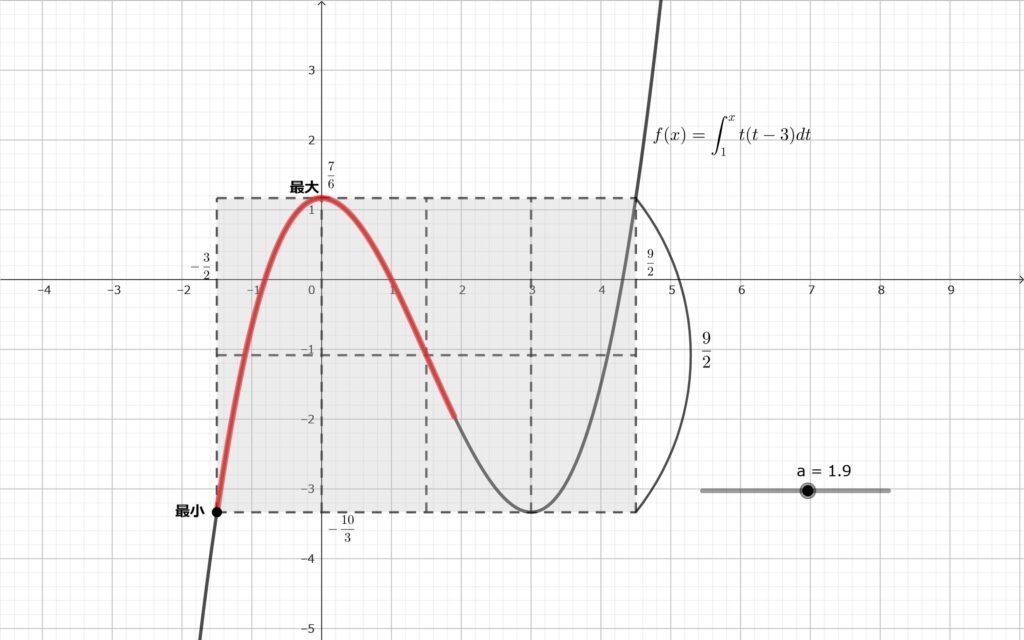
\(\displaystyle 0\leqq s \leqq \frac{9}{2}\) のとき\(,\)
\(x=0\) のとき最大値\(,\) \(\displaystyle x=-\frac{3}{2}\) のとき最小値をとり\(,\) その差は
\begin{align}\frac{7}{6}-\left(-\frac{10}{3}\right)=\frac{9}{2}\end{align}
となり\(,\) 問題文に適する.
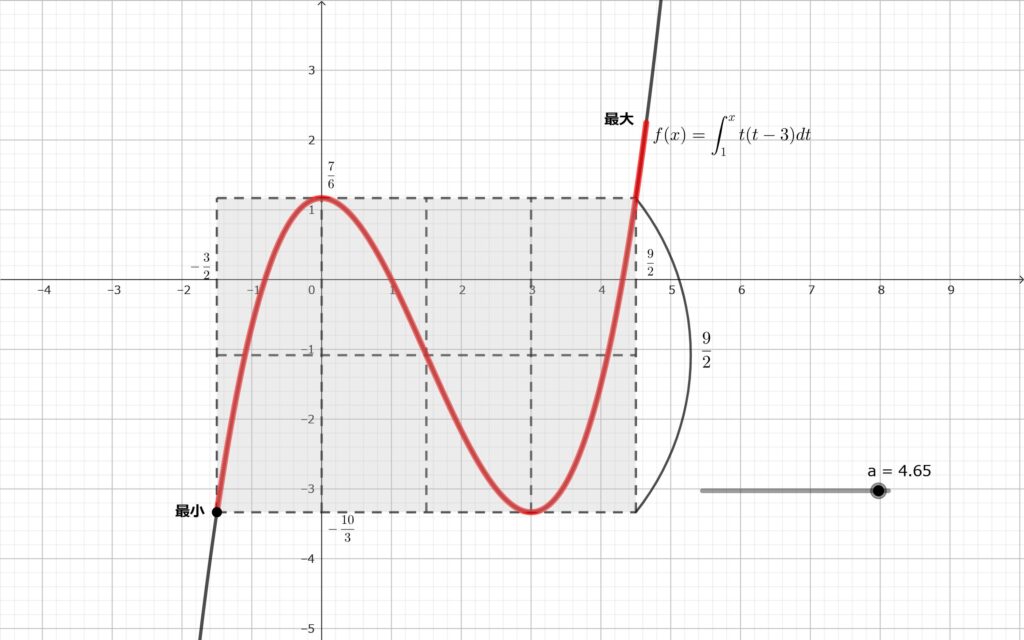
\(\displaystyle s>\frac{9}{2}\) のとき\(,\)
\(x=s\) のとき最大値\(,\) \(\displaystyle x=-\frac{3}{2}\) のとき最小値をとるが\(,\) 上図より\(,\) 最大値と最小値の差は \(\displaystyle \frac{9}{2}\) より大きくなるため不適.
以上より求める\(s\) の範囲は
\begin{align}0\leqq s \leqq \frac{9}{2}~~~~\cdots \fbox{答}\end{align}
ニ:0 ヌ:9 ネ:2





コメント