問題文全文
関数 \(f(x)\) を
\begin{align}f(x)=\frac{x+3}{x^2-4x+29}\end{align}
と定める. 以下の設問に答えよ.
(1) 関数 \(f(x)\) を微分し\(,\) その導関数 \(f^{\prime}(x)\) を既約分数式の形に書き表せ.
(2) \(-10\leqq x\leqq 20\) のとき\(,\) 関数 \(f(x)\) の最大値とそのときの \(x\) の値\(,\) 最小値とそのときの \(x\) の値を求めよ.
(3) 座標平面上で\(,\) 曲線 \(y=f(x)\) と直線 \(\displaystyle y=\frac{1}{5}\) は 2 つの交点をもつ. それらの交点の \(x\) 座標を求めよ.
(4) 座標平面上で\(,\) 曲線 \(y=f(x)\) と直線 \(\displaystyle y=\frac{1}{5}\) によって囲まれた図形の面積を求めよ.
(1) の解答
\(x^2-4x+29=(x-2)^2+25>0\) であるからすべての実数 \(x\) で微分可能である.
\begin{align}f^{\prime}(x)=\frac{x^2-4x+29-(x+3)(2x-4)}{(x^2-4x+29)^2}\end{align}
\begin{align}=\frac{-x^2-6x+41}{(x^2-4x+29)^2}.\end{align}
(2) の解答
\((x^2-4x+29)^2>0\) より\(,\) \(f^{\prime}(x)\) の符号は \(-x^2-6x+41\) の符号のみで決まる.
\begin{align}-x^2-6x+41=0\Leftrightarrow x^2+6x-41=0\end{align}
のとき\(,\)
\begin{align}x=-3\pm 5\sqrt{2}\end{align}
ここで\(,\)
\begin{align}-10-(-3-5\sqrt{2})=5\sqrt{2}-7>5\cdot 1.4-7=0\end{align}
\begin{align}-3+5\sqrt{2}<-3+5\cdot 2=7<20\end{align}
であるから\(,\)
\begin{align}-3-5\sqrt{2}<-10<-3+5\sqrt{2}<20\end{align}

quandle
\(-10\) と \(-3-5\sqrt{2}\) の大小が結構際どいので慎重に判断しましょう.
よって\(,\) 増減表は以下のようになる.
\begin{array}{c|c|c|c|c|c}x & -10 & \cdots & -3+5\sqrt{2} & \cdots & 20 \\ \hline f^{\prime}(x) & {} & + & 0 & – & {} \\ \hline f(x) & \displaystyle -\frac{7}{169} & \nearrow & 最大 & \searrow & \displaystyle \frac{23}{349} \\ \end{array}
\begin{align}f(x)=\frac{x+3}{(x^2+6x-41)-10x+70}\end{align}
より\(,\) 最大値は
\begin{align}f(-3+5\sqrt{2})=\frac{-3+5\sqrt{2}+3}{-10(-3+5\sqrt{2})+70}\end{align}
\begin{align}=\frac{5\sqrt{2}}{100-50\sqrt{2}}=\frac{\sqrt{2}}{20-10\sqrt{2}}\end{align}
\begin{align}=\frac{\sqrt{2}(20+10\sqrt{2})}{200}=\frac{\sqrt{2}+1}{10}\end{align}

quandle
\(x=-3+5\sqrt{2}\) は \(x^2+6x-41=0\) の解ですから\(,\) 多項式 \(x^2+6x-41\) に代入すると \(0\) になります. これを利用することで次数を \(1\) 次式まで下げることができます.
増減表より\(,\)
\(x=-10\) のとき\(,\) 最小値 \(\displaystyle -\frac{7}{169}\).
\(x=-3+5\sqrt{2}\) のとき\(,\) 最大値 \(\displaystyle \frac{\sqrt{2}+1}{10}\).
(3) の解答
\begin{align}\frac{x+3}{x^2-4x+29}=\frac{1}{5}\end{align}
\begin{align}x^2-4x+29=5x+15\end{align}
\begin{align}x^2-9x+14=0\end{align}
\begin{align}(x-2)(x-7)=0\end{align}
\begin{align}x=2,~7.\end{align}
(4) の着眼点
面積の式を立てると以下の式が現れます.
\begin{align}\int_2^7\frac{x+3}{x^2-4x+29}dx\end{align}
分母の 2 次式は実数の範囲で因数分解ができません. (判別式が負です) そういう時は\(,\) 平方完成をすることで必ず \(\displaystyle \frac{1}{x^2+a^2}\) の形に帰着されます.
\(\displaystyle \frac{1}{x^2+a^2}\) の形の積分は \(x=a\tan{\theta}\) と置換することで計算ができます.
上記の置換だけでも計算は可能ですが\(,\) 分母を微分した多項式で分子を割ることで
\begin{align}\int \frac{f^{\prime}(x)}{f(x)}dx=\log{|f(x)|}+C\end{align}
の形が現れるので置換した後の計算が楽になります. (ですが\(,\) 割り算の計算でミスをする可能性が高まるので好みの問題かと思います. 筆者は割り算の解法が好きです.)
(4) の解答
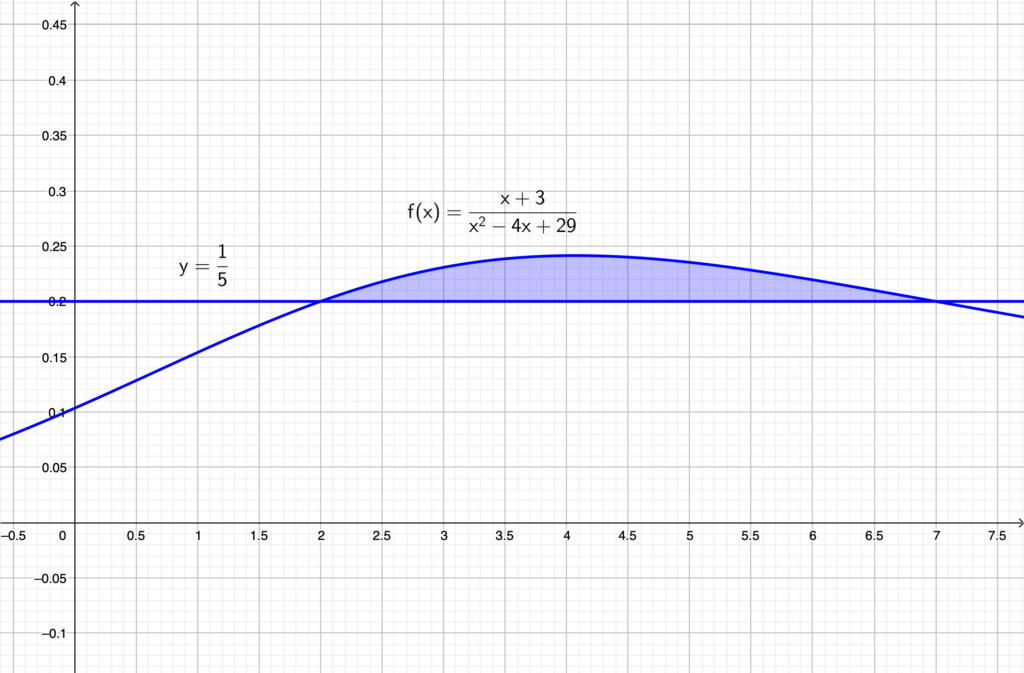
(2) の増減表と (3) より上図のようになる. 求める面積を \(S\) とおくと\(,\)
\begin{align}S=\int_2^7\left(\frac{x+3}{x^2-4x+29}-\frac{1}{5}\right)dx\end{align}
\begin{align}={\Large \int_2^7}\left\{\cfrac{\cfrac{1}{2}(2x-4)+5}{x^2-4x+29}-\frac{1}{5}\right\}dx\end{align}

quandle
分子 \(x+3\) を分母の微分 \(2x-4\) で割りました.
\begin{align}=\biggl[\frac{1}{2}\log{(x^2-4x+29)}-\frac{1}{5}x\biggr]_2^7+\int_2^7\frac{5}{(x-2)^2+25}dx\end{align}

quandle
本来は \(\log\) の真数は絶対値がつきますが\(,\)
\begin{align}x^2-4x+29=(x-2)^2+25>0\end{align}
なので最初から絶対値を外しています.
\begin{align}=\frac{1}{2}(\log{50}-\log{25})-\frac{1}{5}(7-2)+\int_2^7\frac{5}{(x-2)^2+25}dx\end{align}
\begin{align}=\frac{1}{2}\log 2-1+\int_2^7\frac{5}{(x-2)^2+25}dx\end{align}
\(x-2=5\tan{\theta}\) とおく. \(\displaystyle dx=\frac{5}{\cos^2{\theta}}d\theta\)
\begin{array}{c|ccc}x & 2 & \to & 7 \\ \hline \theta & \displaystyle \frac{\pi}{4} & \to & 1\end{array}
\begin{align}S=\frac{1}{2}\log 2-1+\int_0^{\frac{\pi}{4}}\frac{5}{25(1+\cos^2{\theta})}\cdot \frac{5}{\cos^2{\theta}}d\theta\end{align}
\begin{align}=\frac{1}{2}\log 2-1+\int_0^{\frac{\pi}{4}}d\theta =\frac{\pi}{4}+\frac{1}{2}\log 2-1.\end{align}









コメント