2月4日に先進工学部の入試が行われました. 現基礎工学部が2021年4月から先進工学部に名称を変えるようです. 受験された方はお疲れ様でした. 常用対数の問題が最初のアプローチに失敗してなかなかうまくいかなかったです・・・
基礎工学部といえば\(,\) 入学式の途中で北海道まで連行されるのはもはや名物ですね.
微積分以外の問題は手書きではありますがtwitterにて解答速報を出していますのでよろしければご覧ください.
問題文全文
関数
\begin{align}f(x)=\frac{\sqrt{3}}{4}x^2-\frac{\sqrt{3}}{6}\log x-\frac{\sqrt{3}}{4}\log 3~~(x>0)\end{align}
を考える. ただし\(,\) \(\log\) は自然対数とする.
(1) \(f(x)\) は \(\displaystyle 0<x\leqq \frac{\sqrt{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) で単調減少\(,\) \(\displaystyle \frac{\sqrt{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\leqq x\) で単調増加となり\(,\) \(\displaystyle x=\frac{\sqrt{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) で最小値
\begin{align}\frac{\sqrt{\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emエオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\frac{\fbox{$\hskip0.8emカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\log{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
をとる.
(2) 定積分 \(\displaystyle \int_1^3f(x)dx\) の値は\(,\)
\begin{align}\int_1^3f(x)dx=\frac{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\sqrt{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\log{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
となる.
(3) 座標平面上の曲線
\begin{align}y=f(x)~~(1\leqq x\leqq 7)\end{align}
の長さ \(L\) は\(,\)
\begin{align}L=\fbox{$\hskip0.8emセソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}+\frac{\fbox{$\hskip0.8emチ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emツ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\log{\fbox{$\hskip0.8emテ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}
となる.

quandle
すべて入試基礎レベルの計算問題です. 特に着眼点はありません.
(1) の解答
\begin{align}f^{\prime}(x)=\frac{\sqrt{3}}{2}x-\frac{\sqrt{3}}{6x}=\cfrac{\sqrt{3}\left(x-\cfrac{\sqrt{3}}{3}\right)\left(x+\cfrac{\sqrt{3}}{3}\right)}{2x}\end{align}
より\(,\) \(\displaystyle 0<x\leqq \frac{\sqrt{3}}{3}\) で単調減少し\(,\) \(\displaystyle \frac{\sqrt{3}}{3}\leqq x\) で単調増加し\(,\) \(\displaystyle x=\frac{\sqrt{3}}{3}\) のとき最小値
\begin{align}f\left(\frac{\sqrt{3}}{3}\right)=\frac{\sqrt{3}}{4}\cdot \frac{1}{3}-\frac{\sqrt{3}}{6}\left(-\frac{1}{2}\log 3\right)-\frac{\sqrt{3}}{4}\log 3=\frac{\sqrt{3}}{12}-\frac{\sqrt{3}}{6}\log 3.\end{align}
ア:3 イ:3 ウ:3 エ:1 オ:2 カ:3 キ:6 ク:3
(2) の解答
\begin{align}\int_1^3\left(\frac{\sqrt{3}}{4}x^2-\frac{\sqrt{3}}{6}\log x-\frac{\sqrt{3}}{4}\log 3\right)dx\end{align}
\begin{align}=\biggl[\frac{\sqrt{3}}{12}x^3-\frac{\sqrt{3}}{6}(x\log x-x)-\left(\frac{\sqrt{3}}{4}\log 3\right)x\biggr]_1^3\end{align}
\begin{align}=\frac{\sqrt{3}}{12}\cdot 26-\frac{\sqrt{3}}{6}(3\log 3-3+1)-\frac{\sqrt{3}}{2}\log 3\end{align}
\begin{align}=\frac{5}{2}\sqrt{3}-\sqrt{3}\log 3.\end{align}
ケ:5 コ:2 サ:3 シ:3 ス:3
(3) の解答
\begin{align}L=\int_1^7\sqrt{1+\{f^{\prime}(x)\}^2}dx\end{align}
\begin{align}=\int_1^7\sqrt{\frac{3}{4}x^2+\frac{1}{2}+\frac{1}{12x^2}}dx=\int_1^7\sqrt{\left(\frac{\sqrt{3}}{2}x+\frac{1}{2\sqrt{3}x}\right)^2}dx\end{align}
\begin{align}=\int_1^7\left(\frac{\sqrt{3}}{2}x+\frac{1}{2\sqrt{3}x}\right)dx=\biggl[\frac{\sqrt{3}}{4}x^2+\frac{\sqrt{3}}{6}\log x\biggr]_1^7\end{align}
\begin{align}=\frac{\sqrt{3}}{4}\cdot 48+\frac{\sqrt{3}}{6}\log 7=12\sqrt{3}+\frac{\sqrt{3}}{6}\log 7.\end{align}
セ:1 ソ:2 タ:3 チ:3 ツ:6 テ:7
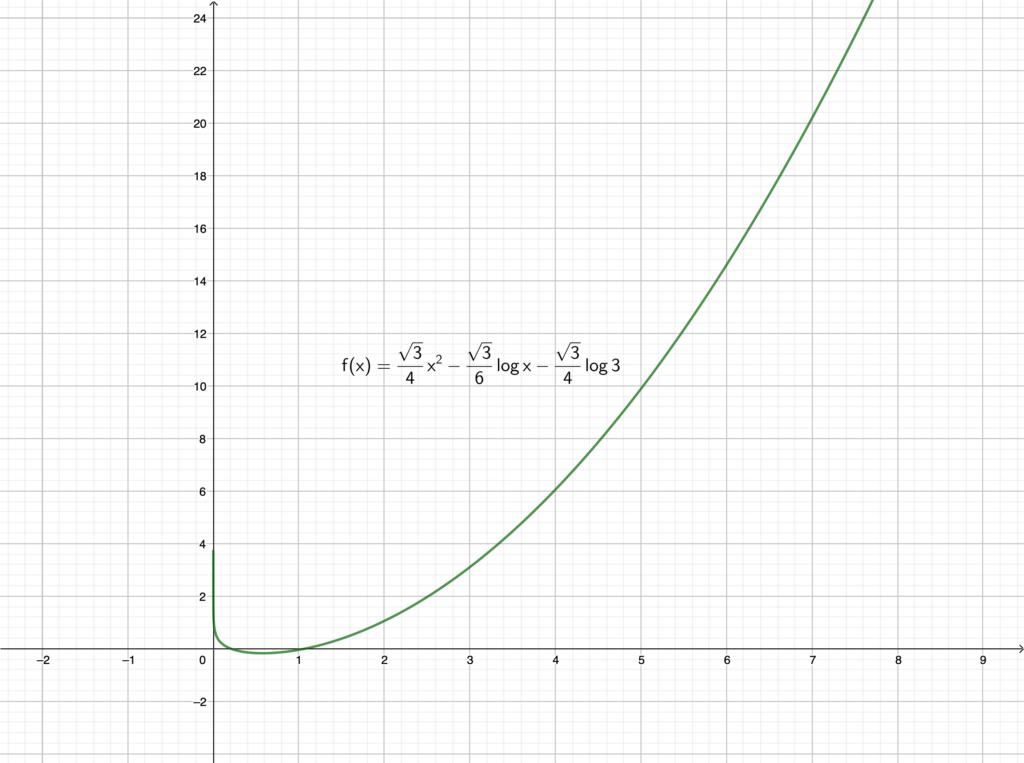
※参考までに \(y=f(x)\) のグラフは以下のようになります.






コメント