問題文全文
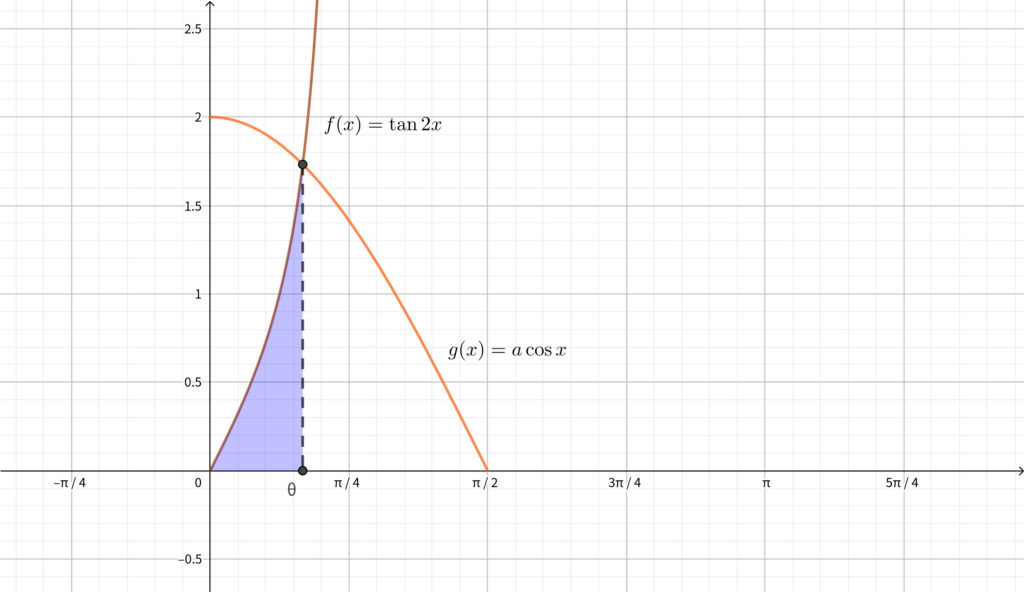
\(a\) を正の定数とし\(,\) 関数 \(\displaystyle f(x)=\tan{2x}~\left(0\leqq x < \frac{\pi}{4}\right)\) および \(\displaystyle g(x)=a\cos{x}~\left(0\leqq x \leqq \frac{\pi}{2}\right)\) に対して\(,\) 曲線 \(y=f(x)\) と \(y=g(x)\) の交点の \(x\) 座標を \(\theta\) とする. 曲線 \(y=f(x)\) と \(x\) 軸\(,\) および直線 \(x=\theta\) で囲まれた部分の面積 \(S\) を考える.
(a) \(a=\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\) のとき\(,\) \(\displaystyle \theta =\frac{\pi}{6}\) である. このとき \(\displaystyle S=\frac{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\times \log{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) である.
(b) \(a=\sqrt{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) のとき\(,\) \(\displaystyle S=\frac{1}{2}\log{\frac{\sqrt{7}+1}{2}}\) である.
ただし\(,\) 正の数 \(A\) に対して\(,\) \(\log{A}\) は \(A\) の自然対数を表す.
(a) の解答
\(\displaystyle \theta =\frac{\pi}{6}\) のとき\(,\)
\begin{align}\tan{\frac{\pi}{3}}=a\cos{\frac{\pi}{6}}\end{align}
\begin{align}\sqrt{3}=\frac{\sqrt{3}}{2}a\end{align}
\begin{align}a=2~~~~\cdots \fbox{答}\end{align}
このとき\(,\)
\begin{align}S=\int_0^{\frac{\pi}{6}}\tan{2x}dx\end{align}
\begin{align}=\biggl[-\frac{1}{2}\log{|\cos{2x}|}\biggr]_0^{\frac{\pi}{6}}=-\frac{1}{2}\log{\frac{1}{2}}\end{align}
\begin{align}=\frac{1}{2}\log{2}~~~~\cdots \fbox{答}\end{align}

quandle
\begin{align}\int \tan{x}dx=-\log{|\cos{x}|}+C\end{align}
は要暗記です.
ア:2 イ:1 ウ:2 エ:2
(b) の解答
\begin{align}S=\int_0^{\theta}\tan{2x}dx\end{align}
\begin{align}=\biggl[-\frac{1}{2}\log{|\cos{2x}|}\biggr]_0^{\theta}=-\frac{1}{2}\log{(\cos{2\theta})}\end{align}

quandle
\(\displaystyle 0<2\theta <\frac{\pi}{2}\) ですから\(,\) \(\cos{2\theta}>0\) が確定するので絶対値は外しています.
\(\displaystyle S=\frac{1}{2}\log{\frac{\sqrt{7}+1}{2}}\) のとき\(,\)
\begin{align}-\frac{1}{2}\log{(\cos{2\theta})}=\frac{1}{2}\log{\frac{\sqrt{7}+1}{2}}\end{align}
\begin{align}\cos{2\theta}=\frac{2}{\sqrt{7}+1}=\frac{\sqrt{7}-1}{3}\end{align}
ここで\(,\)
\begin{align}\tan{2\theta}=a\cos{\theta}\end{align}
より\(,\)
\begin{align}\tan^2{2\theta}=a^2\cos^2{\theta}~~~~\cdots ①\end{align}
であるから\(,\) \(\tan^2{2\theta}\) と \(\cos^2{\theta}\) の値を求めると\(,\)
\begin{align}2\cos^2{\theta}-1=\frac{\sqrt{7}-1}{3}\end{align}
\begin{align}\cos^2{\theta}=\frac{\sqrt{7}+2}{6}\end{align}
\begin{align}1+\tan^2{2\theta}=\frac{1}{\cos^2{2\theta}}\end{align}
\begin{align}\tan^2{2\theta}=\frac{9}{8-2\sqrt{7}}-1\end{align}
\begin{align}\tan^2{2\theta}=\frac{1+2\sqrt{7}}{8-2\sqrt{7}}\end{align}
①に代入して\(,\)
\begin{align}\frac{1+2\sqrt{7}}{8-2\sqrt{7}}=a^2\cdot \frac{\sqrt{7}+2}{6}\end{align}
\begin{align}a^2=\frac{1+2\sqrt{7}}{8-2\sqrt{7}}\cdot \frac{6}{\sqrt{7}+2}\end{align}
\begin{align}=\frac{3(1+2\sqrt{7})}{(4-\sqrt{7})(\sqrt{7}+2)}=\frac{3(1+2\sqrt{7})}{1+2\sqrt{7}}=3\end{align}
\(a>0\) より\(,\)
\begin{align}a=\sqrt{3}~~~~\cdots \fbox{答}\end{align}
オ:3







コメント