経営学部 甲（文系型）2005年第１問(2)の問題文全文
座標平面において\(,\) 放物線 \(C~:~y=x^2\) 上に点 \(\mathrm{P}\) をとり\(,\) 原点と \(\mathrm{P}\) を通る直線を \(\ell \) とする. \(\mathrm{P}\) の \(x\) 座標 \(p\) が \(0<p<1\) の範囲にあるとき\(,\) \(C\) と \(\ell \) で囲まれる部分の面積を \(S_1\) とし\(,\) \(C\) と \(\ell \) と直線 \(x=1\) で囲まれる部分の面積を \(S_2\) とする. \(S_1+S_2\) を最小にする \(p\) は
\begin{align}\frac{1}{\sqrt{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}\end{align}
で\(,\) このとき\(,\) \(S_1+S_2\) の値は
\begin{align}\frac{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\frac{1}{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}\end{align}
である.
着眼点〜\(\frac{1}{6}\) 公式の利用〜
\(S_1\) は放物線と直線で囲まれる部分の面積なので \(\displaystyle \frac{1}{6}\) 公式が使えそうです.
\(S_1\) だけであれば \(\ell \) の方程式がわからなくても面積が出せてしまいますが\(,\) 今回は \(S_2\) を求めるときに必要なので \(\ell \) の方程式を出します.
解答
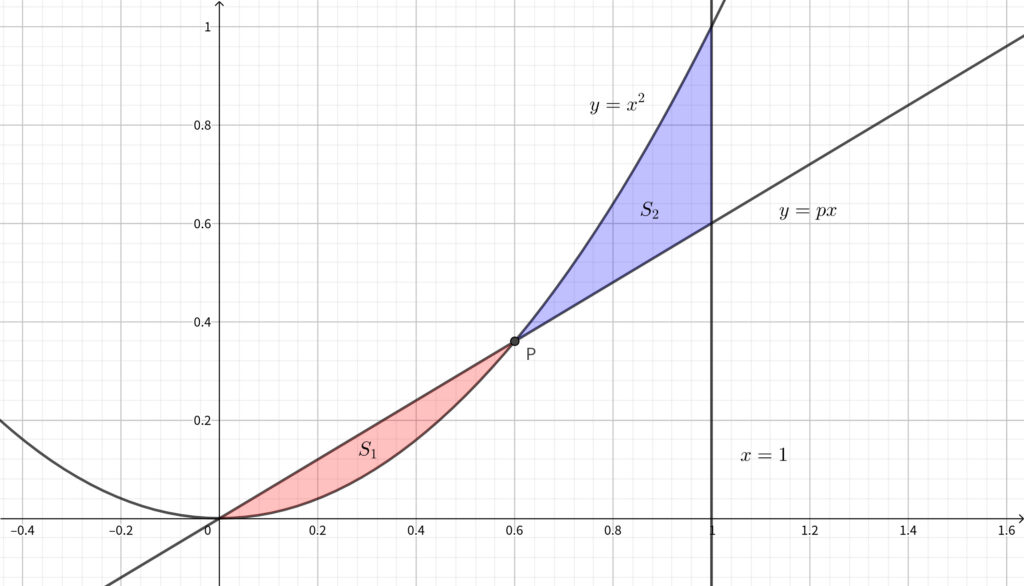
原点 \(\mathrm{O}\) と点 \(\mathrm{P}(p,~p^2)\) を通る直線 \(\ell \) は\(,\) \(y=px\) であるから\(,\)
\begin{align}S_1=\int_0^p(px-x^2)dx\end{align}
\begin{align}=\int_0^p-x(x-p)dx=\frac{1}{6}p^3\end{align}
\begin{align}S_2=\int_p^1(x^2-px)dx\end{align}
\begin{align}=\biggl[\frac{1}{3}x^3-\frac{1}{2}px^2\biggr]_p^1\end{align}
\begin{align}=\frac{1}{3}-\frac{1}{2}p-\left(\frac{1}{3}p^3-\frac{1}{2}p^3\right)\end{align}
\begin{align}=\frac{1}{6}p^3-\frac{1}{2}p+\frac{1}{3}=S(p)\end{align}
とおく.
\begin{align}S^{\prime}(p)=p^2-\frac{1}{2}=\left(p-\frac{1}{\sqrt{2}}\right)\left(p+\frac{1}{\sqrt{2}}\right)\end{align}
\(0<p<1\) より\(,\) \(\displaystyle p+\frac{1}{\sqrt{2}}>0\) であるから\(,\) \(S^{\prime}(p)\) と \(\displaystyle p-\frac{1}{\sqrt{2}}\) の符号は一致する. よって増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline p & 0 & \cdots & \displaystyle \frac{1}{\sqrt{2}} & \cdots & 1 \\ \hline S^{\prime}(p) & {} & – & 0 & + & {} \\ \hline S(p) & {} & \searrow & 極小 & \nearrow & {} \\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}p=\frac{1}{\sqrt{2}}~~~~\cdots \fbox{答}\end{align}
のとき\(,\) 最小値は
\begin{align}S\left(\frac{1}{\sqrt{2}}\right)=\frac{1}{3}\cdot \frac{1}{2\sqrt{2}}-\frac{1}{2}\cdot \frac{1}{\sqrt{2}}+\frac{1}{3}\end{align}
\begin{align}=\frac{1-3+2\sqrt{2}}{6\sqrt{2}}=\frac{\sqrt{2}-1}{3\sqrt{2}}\end{align}
\begin{align}=\frac{1}{3}-\frac{1}{3\sqrt{2}}~~~~\cdots \fbox{答}\end{align}
エ：２ オ：３ カ：３ キ：２
コメント