東京理科大学薬学部2021年第３問

問題文全文
(1) (a) の着眼点
(1) (a) の解答
(1) (b) の着眼点
(1) (b) のgeogebra によるシミュレーション
(1) (b) の解答
(1) (c) の着眼点
(1)(c) の解答
(2) (a) の着眼点
(2) (a) の解答
(2) (b)(c)の着眼点
(2)(b) の解答
(2) (c) の解答

問題文全文

$s,~t$ を実数として$,$ 関数

\begin{align}f(x)=\frac{\sqrt{6}}{3}\sin{x},~g(x)=\frac{\sqrt{2}}{2}x+s,~h(x)=2\sqrt{2}\sin^2{\frac{x}{2}}+t\end{align}

を考える.

(1) (a) ある定数 $k$ があって$,$ $\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ を満たすどのような $x$ に対しても$,$ $f(x)\leqq k \leqq g(x)$ となる最小の $s$ の値は

\begin{align} \frac{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}

である.

(b) $\displaystyle 0 \leqq x \leqq \frac{\pi}{2}$ を満たすある $x$ に対して$,$ ある定数 $l$ があって$,$ $f(x) \leqq l \leqq g(x)$ となる最小の $s$ の値は

\begin{align}\frac{1}{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\frac{1}{\fbox{$\hskip0.8emカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\end{align}

である.

(c) $\displaystyle 0 \leqq x \leqq \frac{\pi}{2}$ を満たすどのような $x$ に対しても$,$ ある定数 $m$ があって$,$ $f(x) \leqq m \leqq g(x)$ となる最小の $s$ の値は

\begin{align}\frac{1}{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\frac{1}{\fbox{$\hskip0.8emコサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\end{align}

である.

(2) (a) $\displaystyle 0\leqq x \leqq \frac{\pi}{2},~0\leqq y \leqq \frac{\pi}{2}$ を満たすどのような $x,~y$ に対しても$,$ $f(x)\leqq h(y)$ となる最小の $t$ の値は

\begin{align}\frac{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}

である.

(b) $\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ を満たすどのような $x$ に対しても$,$ $f(x)\leqq h(x)$ となる最小の $t$ の値は

\begin{align}\frac{\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emチ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emツ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\sqrt{\fbox{$\hskip0.8emテ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}

である.

\begin{align}\frac{\fbox{$\hskip0.8emト\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emナ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8em二\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\sqrt{\fbox{$\hskip0.8emヌ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\end{align}

(1) (a) の着眼点

出てくる文字が $k,~x,~s$ と $3$ つもあるので問題文の解釈が難しいです. あわてず $1$ つずつ固定しながら考えましょう.

「ある定数 $k$ があって」

と言っているので$,$ まずは $k$ を固定して考えます.

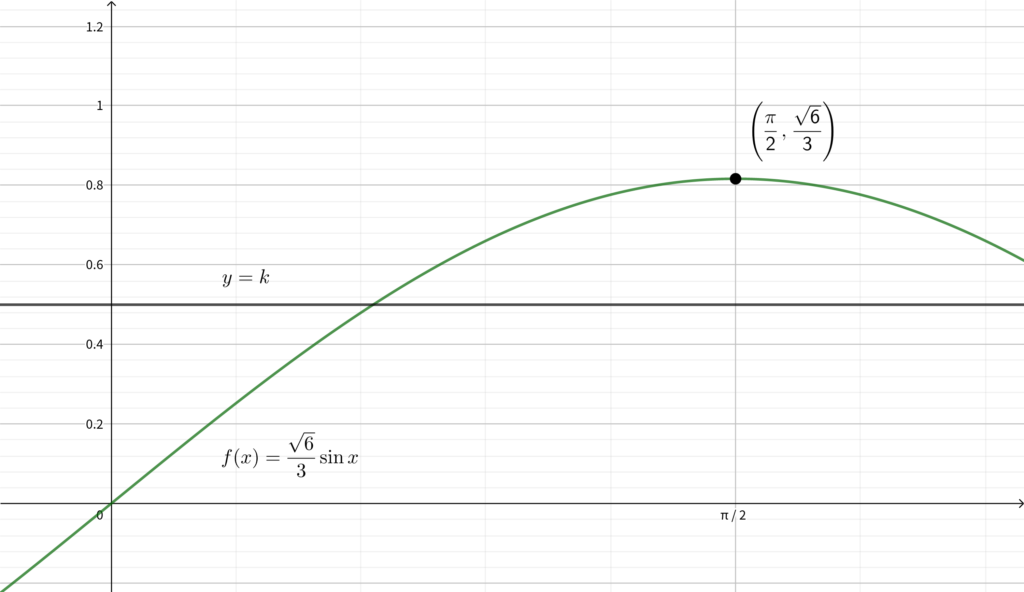
$\displaystyle k<\frac{\sqrt{6}}{3}$ となる $k$ を取ってしまうと$,$ 上図のように

\begin{align}x=\frac{\pi}{2}~のとき~,~k<f(x)\end{align}

となってしまうため$,$ 「どんな $x$ に対しても $f(x) \leqq k$」を満たせません.

よって$,$ $\displaystyle k\geqq \frac{\sqrt{6}}{3}$ であることがわかります.

次に$,$ $\displaystyle k\geqq \frac{\sqrt{6}}{3}$ となる $k$ を固定して$,$ $s$ を動かしてみます.

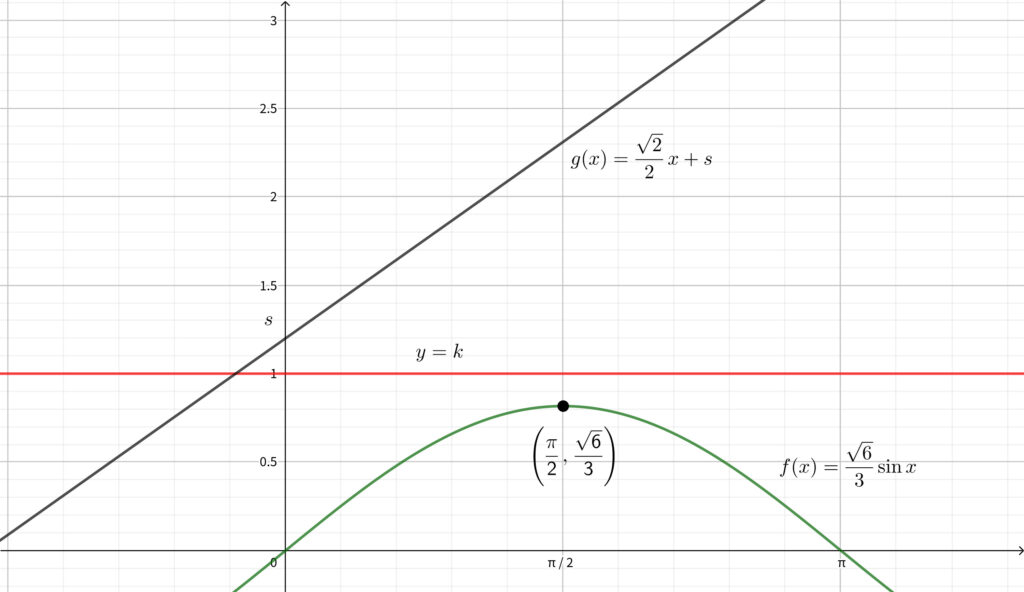
$y=g(x)$ は直線であり$,$ $s$ は $y$ 切片であることを考えると$,$ $k\leqq s$ となる $s$ を取ってくればどんな $x$ に対しても$,$ $k\leqq g(x)$ となることがわかります.

つまり$,$

\begin{align}(f(x)~の最大値)\leqq k \leqq (g(x)~の最小値)\end{align}

が成り立てばよいことがわかります.

(1) (a) の解答

$\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ において$,$

\begin{align}(f(x)~の最大値)\leqq k \leqq (g(x)~の最小値)\end{align}

となればよい.

\begin{align}\frac{\sqrt{6}}{3}\leqq k \leqq s\end{align}

であるから$,$ $s$ の最小値は

\begin{align}\frac{1}{3}\sqrt{6}~~~~\cdots \fbox{答}\end{align}

ア：１　イ：３　ウ：６

(1) (b) の着眼点

「$\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ を満たすある $x$ 」

を $\displaystyle u~\left(0\leqq u \leqq \frac{\pi}{2}\right)$ とおいて$,$ $u$ を固定して考えていきます. このとき$,$

\begin{align}\frac{\sqrt{6}}{3}\sin{u}\leqq l \leqq \frac{\sqrt{2}}{2}u+s\end{align}

を満たす $l$ のうちこの問題を考える上で最適な $l$ を考えます.

「ある $x$ に対して$,$ ある $l$ があって」

と言っているのですから$,$ $u$ を $1$ つ決めるごとに最適な $l$ を決める必要があります.

$u$ は定数ですから$,$

\begin{align}l\leqq \frac{\sqrt{2}}{2}u+s\end{align}

を満たす $s$ は $l$ が大きくなればなるほど大きく取らざるを得ません. 今回は $s$ の最小値が知りたいのですから$,$ $l$ の値はできるだけ小さくあってほしいということになります.

つまり$,$ 各 $u$ に対する $l$ として最適なのは最小値である

\begin{align}l=\frac{\sqrt{6}}{3}\sin{u}\end{align}

となります. このとき$,$

\begin{align}s\geqq \frac{\sqrt{6}}{3}\sin{u}-\frac{\sqrt{2}}{2}u\end{align}

ですから$,$ $s$ の最小値は $\displaystyle \frac{\sqrt{6}}{3}\sin{u}-\frac{\sqrt{2}}{2}u$ です.

あとは固定していた $u$ を動かして$,$ $s$ の最小値を求めます.

(1) (b) のgeogebra によるシミュレーション

$u$ がスライダーで動かせるようになっています. また$,$ $s$ である $y=g(x)$ の $y$ 切片が残像で残るように設定しているので $s$ が $\displaystyle u=\frac{\pi}{2}$ で最小値をとる様子も確認できます.

quandle

今回は穴埋め問題ですから $\displaystyle u=\frac{\pi}{2}$ で最小値をとることが視覚的にも明らかなので$,$ さっさと代入して答えを求めてしまいましょう. 以下の解答では一応きちんと微分法を用いて調べてみました.

(1) (b) の解答

$\displaystyle u~\left(0\leqq u \leqq \frac{\pi}{2}\right)$ に対して$,$

\begin{align}\frac{\sqrt{6}}{3}\sin{u}\leqq l \leqq \frac{\sqrt{2}}{2}u+s\end{align}

を満たす $l$ を考える. $s$ の最小値を考えたいので$,$

\begin{align}l=\frac{\sqrt{6}}{3}\sin{u}\end{align}

を選べば十分である. このとき$,$

\begin{align}s\geqq \frac{\sqrt{6}}{3}\sin{u}-\frac{\sqrt{2}}{2}u\end{align}

であるから$,$ 右辺の最小値が求める $s$ の最小値である.

\begin{align}F(u)=\frac{\sqrt{6}}{3}\sin{u}-\frac{\sqrt{2}}{2}u\end{align}

とおく. $\displaystyle \left(0\leqq u \leqq \frac{\pi}{2}\right)$

\begin{align}F^{\prime}(u)=\frac{\sqrt{6}}{3}\cos{u}-\frac{\sqrt{2}}{2}\end{align}

\begin{align}\begin{array}{|c|c|c|c|c|c|} \hline u & 0 & \cdots & \displaystyle \frac{\pi}{3} & \cdots & \displaystyle \frac{\pi}{2}\\ \hline F^{\prime}(u) & {} & + & 0 & – & {} \\ \hline F(u) & 0 & \nearrow & \displaystyle F\left(\frac{\pi}{3}\right) & \searrow & \displaystyle F\left(\frac{\pi}{2}\right) \\ \hline \end{array}\end{align}

\begin{align}F\left(\frac{\pi}{2}\right)=\frac{\sqrt{6}}{3}\cdot 1 -\frac{\sqrt{2}}{2}\cdot \frac{\pi}{2}\end{align}

\begin{align}=\frac{\sqrt{6}}{3}-\frac{\sqrt{2}}{4}\pi=\frac{\sqrt{2}}{12}(4\sqrt{3}-3\pi)\end{align}

\begin{align}<\frac{\sqrt{2}}{12}(4\cdot 2-3\cdot 3)=-\frac{\sqrt{2}}{12}<0~(=F(0))\end{align}

quandle

増減表より$,$ 最小値の候補が $2$ つあります. $\displaystyle F\left(\frac{\pi}{2}\right)$ が最小値であることを言うために $\displaystyle F\left(\frac{\pi}{2}\right)<F(0)$ であることを強調して書いています.

よって求める $s$ の最小値は

\begin{align}s=\frac{1}{3}\sqrt{6}-\frac{1}{4}{\sqrt{2}}\pi~~~~\cdots \fbox{答}\end{align}

エ：３　オ：６　カ：４　キ：２　

(1) (c) の着眼点

「どのような $x$ に対しても$,$ ある定数 $m$ があって」

この表現に不慣れだという人も多いかと思います. これは

「$x$ ごとに取ってくる定数 $m$ は違うものでいい」

ということです.

「$x$ を一つ決めたときに$,$ 条件をみたす $m$ が最低 $1$ 個取れればいい」

という意味です.

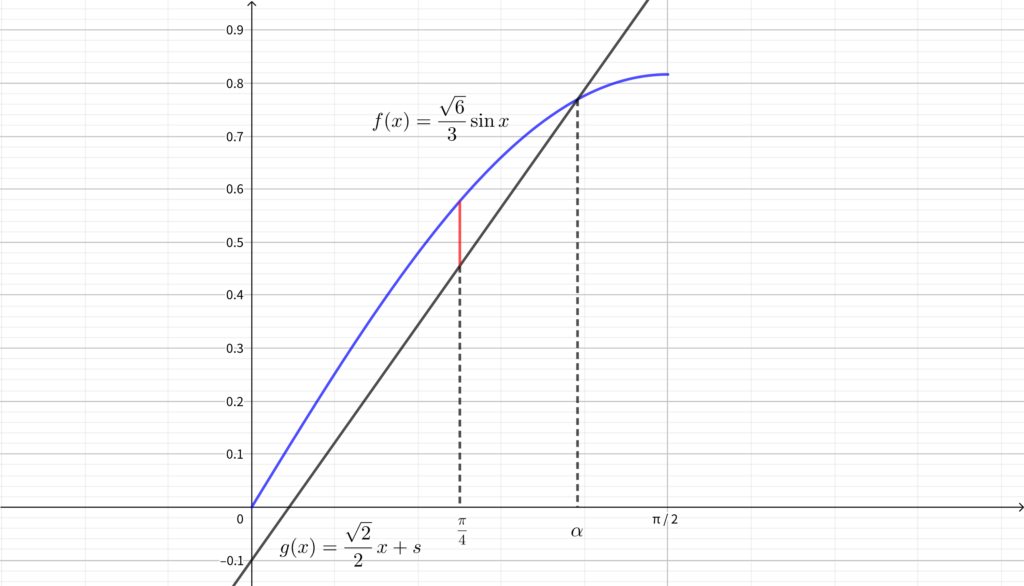
例えば $y=f(x)$ と $y=g(x)$ のグラフが上図のような位置関係だとすると$,$

$\displaystyle x=\frac{\pi}{4}$ のとき$,$ $f(x)>g(x)$ となってしまっているので$,$ 題意を満たしません. （任意の $x$ について $f(x)\leqq g(x)$ でなければならないので$,$ 反例となってしまっています.）

上の考察から交わってはいけなさそうです. 交わらないようにすると以下の図のようになります.

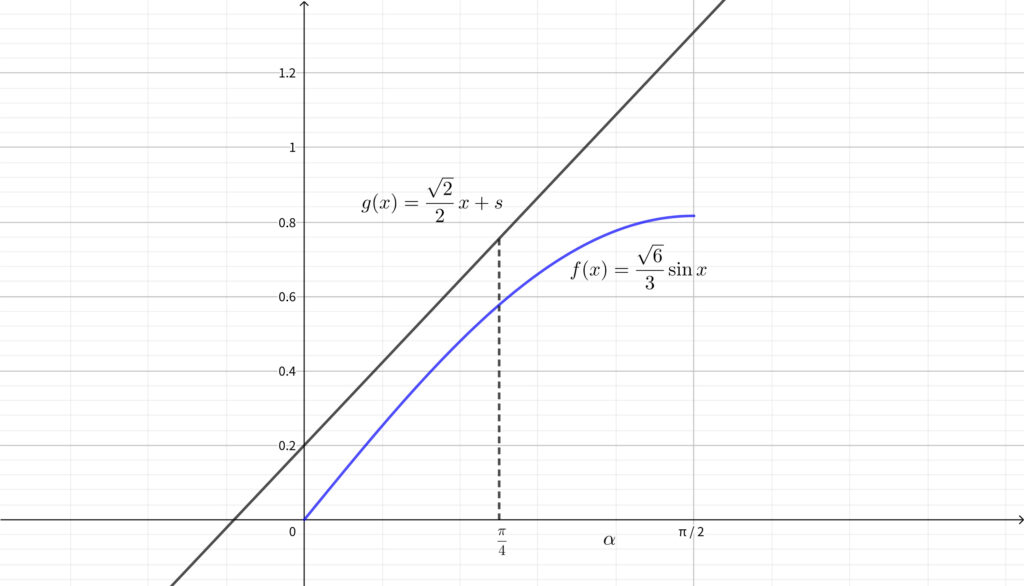
上図のようなときは例えば

$x=0$ のときは $m=0.1$$,$ $\displaystyle x=\frac{\pi}{4}$ のときは $m=0.6$

のように $x$ を一つ決めるごとに $m$ を一つ決めて（同じ値でなくてよい）

\begin{align}f(x)\leqq m \leqq g(x)\end{align}

とできることがわかります.

では$,$ $s$ が最小となるのはどこでしょうか？もちろん接するときです.

(1)(c) の解答

$y=f(x)$ と $y=g(x)$ のグラフが接するときの $s$ を求めれば良い.

$x=\alpha $ のとき接するとすると$,$ $\displaystyle f^{\prime}(x)=\frac{\sqrt{6}}{3}\cos{x}$ より$,$

\begin{align}f^{\prime}(\alpha )=\frac{\sqrt{6}}{3}\cos{\alpha}=\frac{\sqrt{2}}{2}\end{align}

\begin{align}\alpha =\frac{\pi}{6}\end{align}

このとき$,$ $f(\alpha )=g(\alpha )$ より$,$

\begin{align}\frac{\sqrt{6}}{3}\cdot \frac{1}{2}=\frac{\sqrt{2}}{2}\cdot \frac{\pi}{6}+s\end{align}

\begin{align}s=\frac{1}{6}\sqrt{6}-\frac{1}{12}\sqrt{2}\pi~~~~\cdots \fbox{答}\end{align}

ク：６　ケ：６　コ：１　サ：２　シ：２

(2) (a) の着眼点

「どのような $x, y$ に対しても」

とあり$,$ 文字が $2$ つとも自由に動いてしまっているので$,$ 何か $1$ つ $x$ を取ってきて固定します. 例えば $x=0$ をとってきて固定すると$,$ $f(0)=0$ ですから$,$

「$\displaystyle 0\leqq y \leqq \frac{\pi}{2}$ であるどのような $y$ に対しても $0\leqq h(y)$」

となるように $t$ を決める問題となります. これならよくある問題なので$,$ 自然と $h(y)$ の最小値に目が行くのではないでしょうか. つまり$,$

「$h(y)$ の最小値 $\geqq 0$」

となるように $t$ を決めることになります.

$x$ を自由に動かしたときも$,$ その都度 $h(y)$ の最小値と比較すればよいのですから$,$

「$f(x)$ の最大値 $\leqq $ $h(x)$ の最小値」

とすればすべての$x,~y$ について保証することができます.

(2) (a) の解答

$\displaystyle 0\leqq x \leqq \frac{\pi}{2},~0\leqq y \leqq \frac{\pi}{2}$ を満たすどのような $x,~y$ に対しても$,$ $f(x)\leqq h(y)$ となるための必要十分条件は

\begin{align}f(x)~の最大値 \leqq h(x)~の最小値\end{align}

である. $f(x),~g(x)$ はともに $\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ において$,$ 明らかに単調増加な関数であるから$,$

\begin{align}f\left(\frac{\pi}{2}\right)\leqq h(0)\end{align}

となればよい.

\begin{align}f\left(\frac{\pi}{2}\right)=\frac{\sqrt{6}}{3},~h(0)=t\end{align}

であるから$,$

\begin{align}\frac{\sqrt{6}}{3}\leqq t\end{align}

この不等式を満たす最小の $t$ の値は

\begin{align}t=\frac{1}{3}\sqrt{6}~~~~\cdots \fbox{答}\end{align}

ス：１　セ：３　ソ：６

(2) (b)(c)の着眼点

\begin{align}F(x)=h(x)-f(x)=2\sqrt{2}\sin^2{\frac{x}{2}}+t-\frac{\sqrt{6}}{3}\sin{x}\end{align}

とおくと$,$

(b) は $\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ となるすべての $x$ に対して$,$ $F(x)\geqq 0$

を満たせばよいことになります.

(b) は $F(x)$ の最小値が $0$ 以上であればいいですし$,$ (c) は $F(x)$ の最大値が $0$ 以上であれば題意を満たすことがわかります.

(2)(b) の解答

\begin{align}F(x)=h(x)-f(x)=2\sqrt{2}\sin^2{\frac{\pi}{2}}+t-\frac{\sqrt{6}}{3}\sin{x}\end{align}

\begin{align}=\sqrt{2}(1-\cos{x})+t-\frac{\sqrt{6}}{3}\sin{x}=t+\sqrt{2}-\frac{2\sqrt{6}}{3}\sin{\left(x+\frac{\pi}{3}\right)}\end{align}

とおく.

$\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ を満たすどのような $x$ に対しても$,$ $f(x)\leqq h(x)$ となるための必要十分条件は

\begin{align}(F(x)~の最小値~) \geqq 0\end{align}

となることである.

$\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ より$,$ $\displaystyle \frac{\pi}{3}\leqq x+\frac{\pi}{3}\leqq \frac{5}{6}\pi$ であるから$,$

\begin{align}\frac{1}{2}\leqq \sin{\left(x+\frac{\pi}{3}\right)}\leqq 1\end{align}

\begin{align}-\frac{2\sqrt{6}}{3}\leqq -\frac{2\sqrt{6}}{3}\sin{\left(x+\frac{\pi}{3}\right)}\leqq -\frac{\sqrt{6}}{3}\end{align}

\begin{align}t+\sqrt{2}-\frac{2\sqrt{6}}{3}\leqq F(x) \leqq t+\sqrt{2}-\frac{\sqrt{6}}{3}\end{align}

$F(x)$ の最小値は

\begin{align}t+\sqrt{2}-\frac{2\sqrt{6}}{3}\end{align}

であるから$,$

\begin{align}t+\sqrt{2}-\frac{2\sqrt{6}}{3}\geqq 0\end{align}

\begin{align}t\geqq \frac{2\sqrt{6}}{3}-\sqrt{2}~~~~\cdots \fbox{答}\end{align}

タ：２　チ：３　ツ：６　テ：２

(2) (c) の解答

$\displaystyle 0\leqq x \leqq \frac{\pi}{2}$ を満たすある $x$ に対して$,$ $f(x)\leqq h(x)$ となるための必要十分条件は

\begin{align}(F(x)~の最大値~)\geqq 0\end{align}

となることである. (2)(b) より$,$ $F(x)$ の最大値は

\begin{align}t+\sqrt{2}-\frac{\sqrt{6}}{3}\end{align}

であるから$,$

\begin{align}t+\sqrt{2}-\frac{\sqrt{6}}{3}\geqq 0\end{align}

\begin{align}t\geqq \frac{1}{3}\sqrt{6}-\sqrt{2}~~~~\cdots \fbox{答}\end{align}

ト：１　ナ：３　ニ：６　ヌ：２