\(\displaystyle \frac{1}{6}\) 公式とは
\(\displaystyle \int_{\alpha}^{\beta}(x-\alpha )(x-\beta )dx=-\frac{1}{6}(\beta -\alpha )^3\)
は \(\displaystyle \frac{1}{6}\) 公式と呼ばれています. 裏技として紹介されることもありますが\(,\) 裏技でもなんでもなく\(,\) 教科書にも載っている必ず身につけておくべき公式です.
「この公式を使うことで時短をする」のではなく\(,\) この公式が使えることは当たり前で\(,\) 「使えない場合かなりの時間をロスしてしまうもの」という感覚のほうが正しいと思っています.
理科大の入試問題もこの公式を使うことを前提に時間配分が設定されていると感じます. 確実に使えるように練習しておきましょう. また\(,\) 以下に記載する証明が自力でできることが大事です. 必ず自力でできるまで反復練習しておきましょう. 証明の変形が問題となっていることもあるからです.
\(\displaystyle \frac{1}{6}\) 公式の証明
証明①（推奨の変形）
\begin{align}\int_{\alpha}^{\beta}(x-\alpha )(x-\beta )dx=\int_{\alpha}^{\beta}(x-\alpha )\{(x-\alpha )+(\alpha -\beta )\}dx\end{align}
\begin{align}=\int_{\alpha}^{\beta}(x-\alpha )^2dx+(\alpha -\beta)\int_{\alpha}^{\beta}(x-\alpha )dx\end{align}
\begin{align}=\biggl[\frac{1}{3}(x-\alpha )^3\biggr]_{\alpha}^{\beta}+(\alpha -\beta )\biggl[\frac{1}{2}(x-\alpha )^2\biggr]_{\alpha}^{\beta}\end{align}
\begin{align}=\frac{1}{3}(\beta -\alpha )^3-\frac{1}{2}(\beta -\alpha )^3=-\frac{1}{6}(\beta -\alpha )^3\end{align}
quandle
\(x-\beta =(x-\alpha ) +(\alpha -\beta )\)
と見る変形がポイントです.
証明②（非推奨ですが１度はやっておきましょう）
\begin{align}\int_{\alpha}^{\beta}(x-\alpha )(x-\beta )dx=\int_{\alpha}^{\beta}\{x^2-(\alpha +\beta )x+\alpha \beta \}dx\end{align}
\begin{align}=\biggl[\frac{1}{3}x^3-\frac{1}{2}(\alpha +\beta )x^2+\alpha \beta x\biggr]_{\alpha}^{\beta}\end{align}
\begin{align}=\frac{1}{3}({\beta}^3 -{\alpha}^3)-\frac{1}{2}(\alpha +\beta )({\beta}^2-{\alpha}^2)+\alpha \beta(\beta -\alpha )\end{align}
\begin{align}=-\frac{1}{6}(\beta -\alpha )\{-2({\beta}^2+\alpha \beta +{\alpha}^2)+3({\alpha}^2+2\alpha \beta +{\beta}^2)-6\alpha \beta\}\end{align}
\begin{align}=-\frac{1}{6}(\beta -\alpha )({\beta}^2-2\alpha \beta +{\alpha}^2)=-\frac{1}{6}(\beta -\alpha )^3\end{align}
面積への応用
\(\displaystyle \frac{1}{6}\) 公式が真の力を発揮するのは面積の計算のときです.
大きく分けて次の場合には積分計算を省略して面積を求めることができるため非常に便利です.
① 放物線と直線で囲まれた部分の面積
② 放物線と放物線で囲まれた部分の面積
放物線と直線で囲まれた部分の面積
放物線と直線が異なる \(2\) 点で交わるとき\(,\) 囲まれた部分の面積を \(\displaystyle \frac{1}{6}\) 公式を用いて求めることができます. 具体的には以下のような図になるときの面積です.
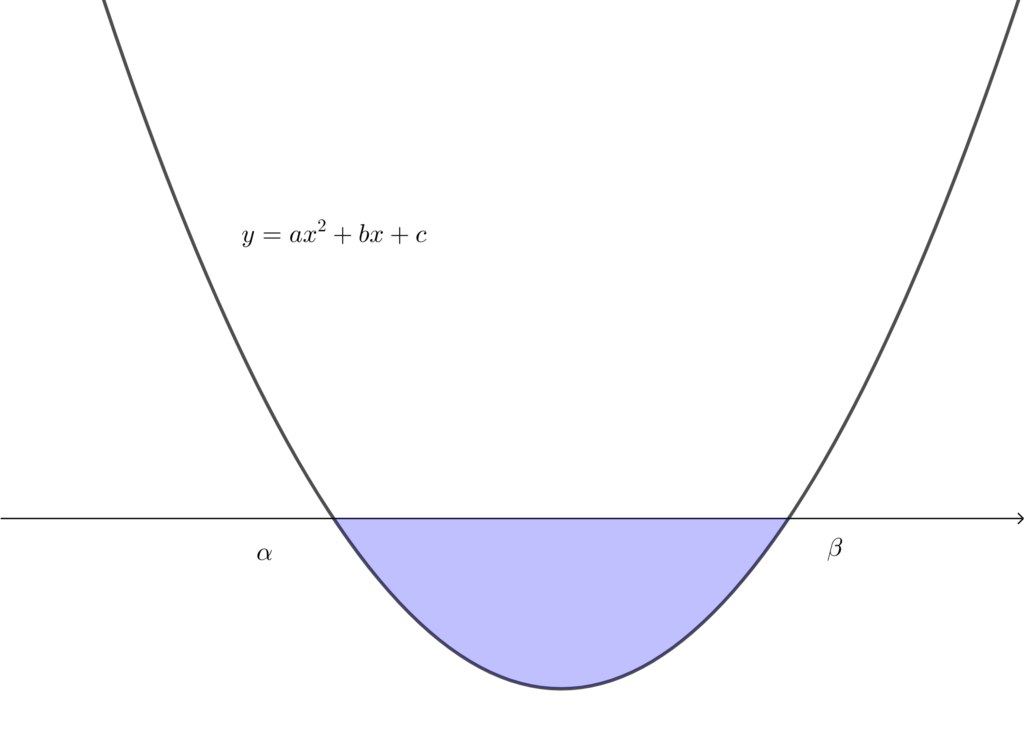下に凸の放物線と \(x\) 軸で囲まれた部分の面積
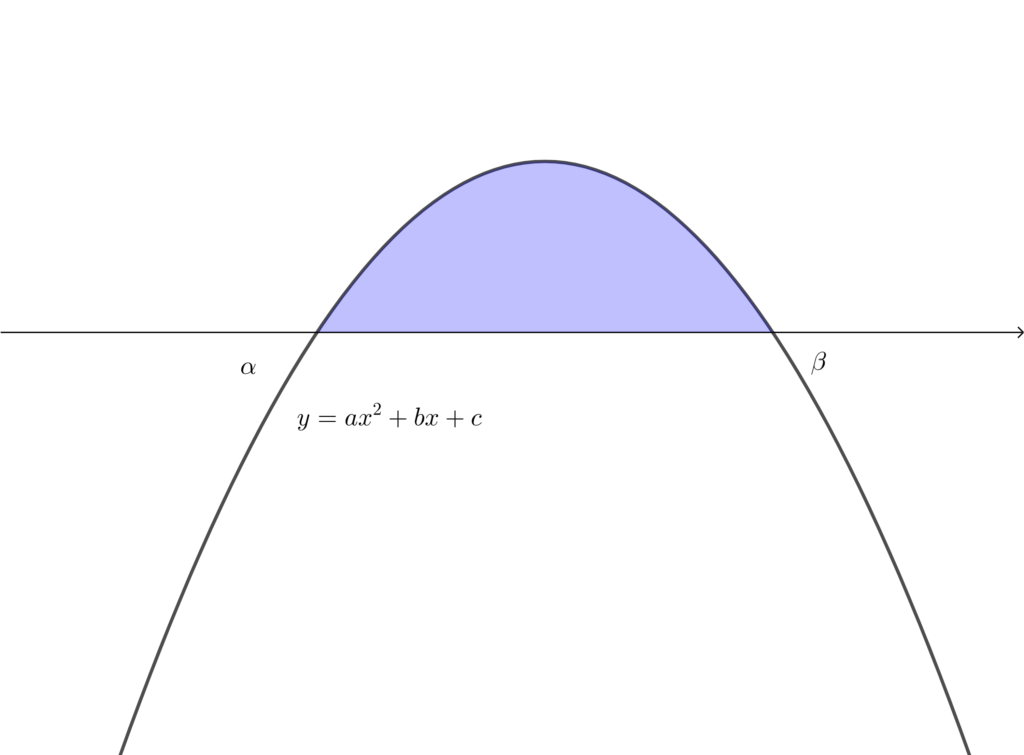上に凸の放物線と \(x\) 軸で囲まれた部分の面積
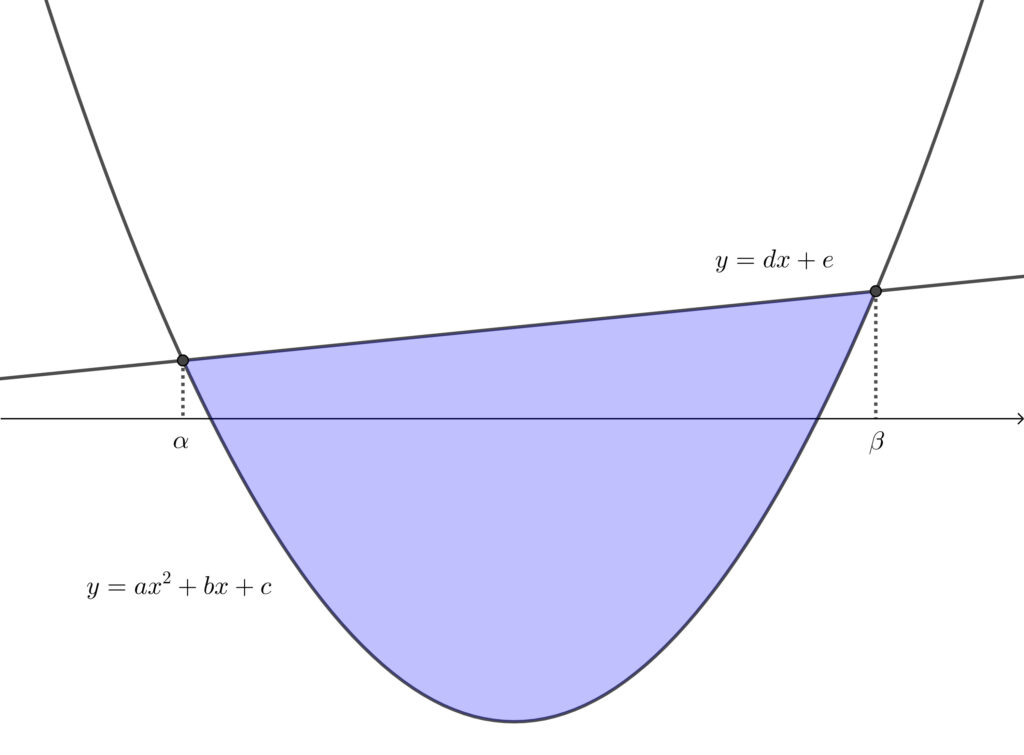下に凸の放物線と直線で囲まれた部分の面積
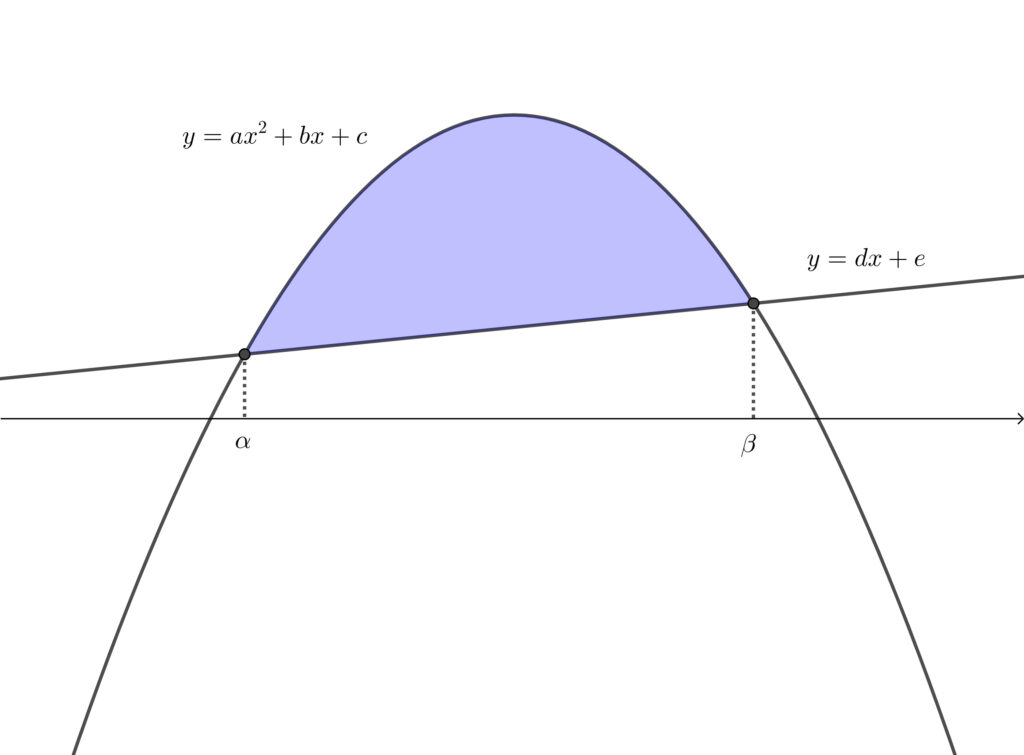上に凸の放物線と直線で囲まれた部分の面積
一般に放物線 \(y=ax^2+bx+c\) と直線 \(y=dx+e\) が異なる \(2\) 点で交わるとき\(,\) その交点の \(x\) 座標は連立方程式
\begin{align}ax^2+bx+c=dx+e\end{align}
の \(2\) 解で与えられます. その \(2\) 解を \(\alpha ,~\beta \) とおくと\(,\)
\(a>0\) のとき（下に凸の放物線のとき）
\begin{align}\int_{\alpha}^{\beta}\{dx+e-(ax^2+bx+c)\}dx=-a\int_{\alpha}^{\beta}(x-\alpha )(x-\beta )dx\end{align}
\begin{align}=-a\left\{-\frac{1}{6}(\beta -\alpha )^3\right\}=\frac{a}{6}(\beta -\alpha )^3\end{align}
\(a<0\) のとき（上に凸の放物線のとき）
\begin{align}\int_{\alpha}^{\beta}\{ax^2+bx+c-(dx+e)\}dx=a\int_{\alpha}^{\beta}(x-\alpha )(x-\beta )dx\end{align}
\begin{align}=-\frac{a}{6}(\beta -\alpha )^3\end{align}
quandle
\(a<0\) ですから\(,\) \(\displaystyle -\frac{a}{6}>0\) ですね！
で与えられるため\(,\) いずれの場合も
\begin{align}\frac{|a|}{6}(\beta -\alpha )^3\end{align}
で面積を計算することができます.
放物線と放物線で囲まれる部分の面積
\(2\) つの放物線で囲まれた部分の面積を求めるときにも \(\displaystyle \frac{1}{6}\) 公式を利用でき\(,\) 積分計算を省略することができます. 具体的には以下の図のようになるときです.
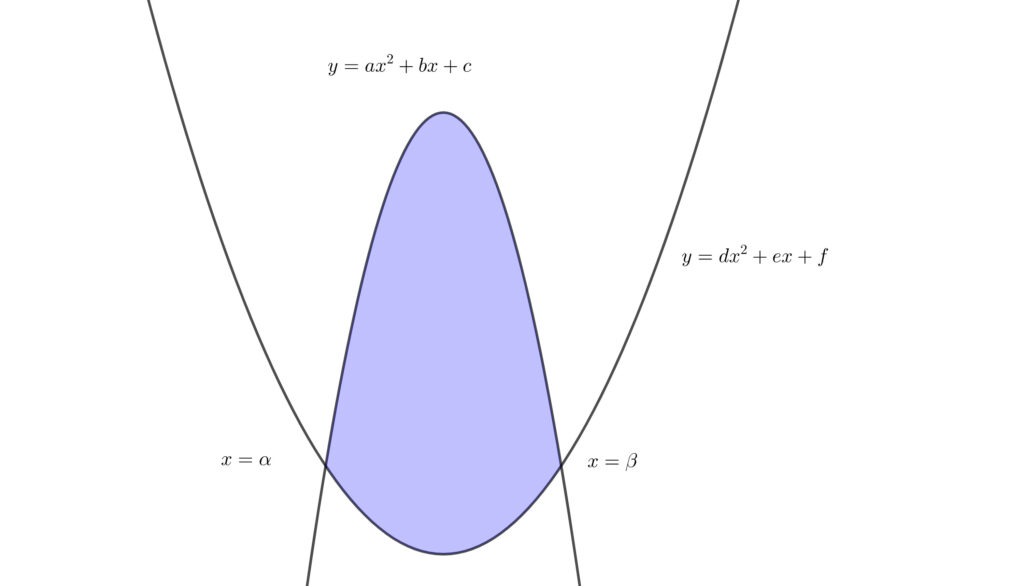上に凸の放物線と下に凸の放物線で囲まれた部分
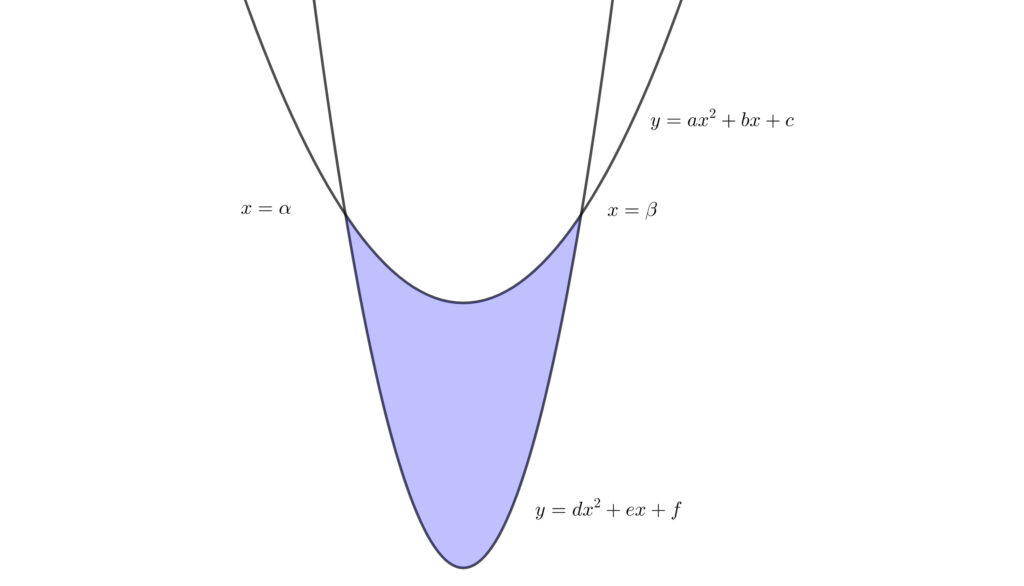2 つの下に凸の放物線で囲まれた部分
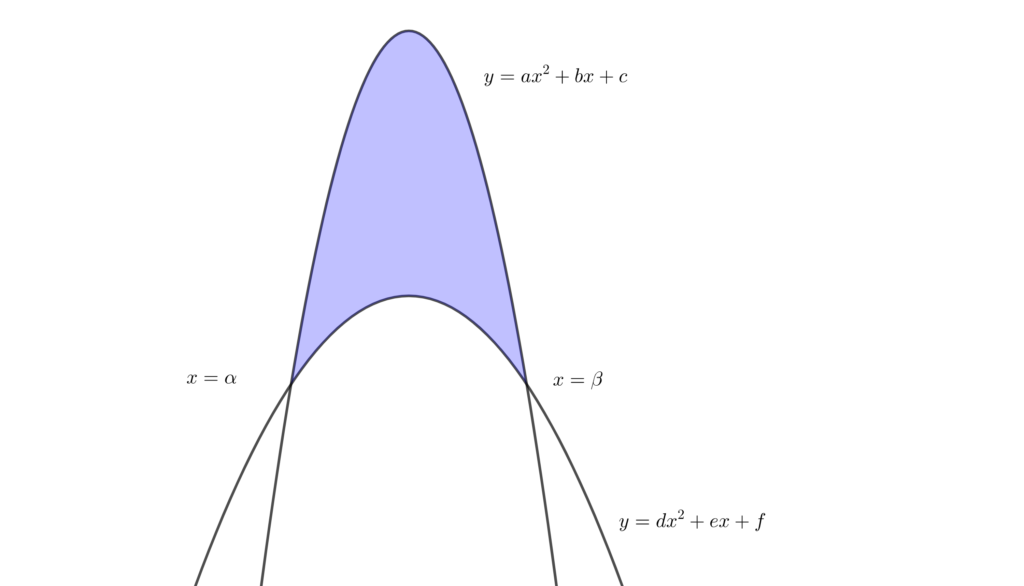2 つの上に凸の放物線で囲まれた部分
\(2\) つの放物線をそれぞれ\(,\) \(y=ax^2+bx+c,~y=dx^2+ex+f~(a<d)\) とおく. \(2\) つの放物線が異なる \(2\) 点で交わる場合を考えます.
\(a<d\) なので上図のどの場合においても上側の曲線は \(y=ax^2+bx+c\) であり\(,\) 下側の曲線は \(y=dx^2+ex+f\) となります.
また\(,\) \(2\) つの放物線の交点 の \(x\) 座標は連立方程式
\begin{align}ax^2+bx+c=dx^2+ex+f\end{align}
の \(2\) 解で与えられます. その \(2\) 解を \(\alpha ,~\beta\) とおくと\(,\) \(2\) つの放物線で囲まれた部分の面積は
\begin{align}\int_{\alpha}^{\beta}\{ax^2+bx+c-(dx^2+ex+f)\}dx=(a-d)\int_{\alpha}^{\beta}(x-\alpha )(x-\beta )dx\end{align}
\begin{align}=(a-d)\left\{-\frac{1}{6}(\beta -\alpha )^3\right\}=\frac{d-a}{6}(\beta -\alpha )^3\end{align}
となるので\(,\) \(\displaystyle \frac{1}{6}\) 公式を利用して面積が計算できることが分かります.
また\(,\) \(a<d\) より \(d-a>0\) なので\(,\) ちゃんと正の値で面積が計算されることも分かります.
練習問題〜理科大の過去問に挑戦〜
\(\displaystyle \frac{1}{6}\) 公式を利用する過去問を集めました. 挑戦してみてください.
経営学部（経営学科選択問題）2020年第３問
理工学部（数・物・情・応生・経営工）2021年第３問
コメント