先進工学部2022年第2問の問題文全文 関数
\begin{align}y=\sin^3{x}+\cos^3{x}+3\sin{x}\cos{x}-2\sin{x}-2\cos{x}-1~(0\leqq x < 2\pi )\end{align}
を考える.
(1) \(t=\sin{x}+\cos{x}\) とおくとき\(,\)
\begin{align}\sin{x}\cos{x}=\frac{t^{^{~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}}~-~\fbox{$\hskip0.4emイ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{\fbox{$\hskip0.4emウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}~,~\sin^3{x}+\cos^3{x}=\frac{-t^{^{~\fbox{$\hskip0.4emエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}}~+~\fbox{$\hskip0.4emオ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~t}{\fbox{$\hskip0.4emカ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}\end{align}
となるので\(,\) \(y\) を \(t\) の式で表すと\(,\)
\begin{align}y=-~\frac{\fbox{$\hskip0.4emキ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{\fbox{$\hskip0.4emク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}~t^3+~\frac{\fbox{$\hskip0.4emケ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{\fbox{$\hskip0.4emコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}~t^2-~\frac{\fbox{$\hskip0.4emサ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{\fbox{$\hskip0.4emシ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}~t-\frac{\fbox{$\hskip0.4emス\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{\fbox{$\hskip0.4emセ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}\end{align}
である.
(2) (1) で定めた \(t\) のとり得る値の範囲は\(,\)
\begin{align}-\sqrt{~\fbox{$\hskip0.4emソ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\leqq t \leqq \sqrt{~\fbox{$\hskip0.4emタ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である.
(3) \(y\) のとり得る値の範囲は\(,\)
\begin{align}-~\fbox{$\hskip0.4emチ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~-~\frac{\fbox{$\hskip0.4emツ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{\fbox{$\hskip0.4emテ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}~\sqrt{~\fbox{$\hskip0.4emト\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~\leqq y \leqq ~\frac{\fbox{$\hskip0.4emナ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{2}~+~\frac{\fbox{$\hskip0.4emニ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{2}~\sqrt{~\fbox{$\hskip0.4emヌ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である.
(4) 異なる \(2\) つの \(x\) の値で \(y=0\) となる. \(1\) つは \(x=\pi \) であり\(,\) もう \(1\) つは \(\displaystyle x=~\frac{\fbox{$\hskip0.4emネ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}{\fbox{$\hskip0.4emノ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}~\pi\) である.
(1) の解答〜三角関数の対称式〜 \(\sin{x}\cos{x}\) を \(t\) で表す.
\begin{align}t=\sin{x}+\cos{x}\end{align}
\begin{align}t^2=1+2\sin{x}\cos{x}\end{align}
\begin{align}\sin{x}\cos{x}=\frac{t^2-1}{2}~~~~\cdots \fbox{答}\end{align}
\(\sin^3{x}+\cos^3{x}\) を \(t\) で表す〜因数分解の利用〜
\begin{align}\sin^3{x}+\cos^3{x}=(\sin{x}+\cos{x})(1-\sin{x}\cos{x})\end{align}
\begin{align}=t\left(1-\frac{t^2-1}{2}\right)=\frac{-t^3+3t}{2}~~~~\cdots \fbox{答}\end{align}
\(\sin^3{x}+\cos^3{x}\) の別解〜対称式の変形の利用〜
\begin{align}\sin^3{x}+\cos^3{x}=(\sin{x}+\cos{x})^3-3\sin{x}\cos{x}(\sin{x}+\cos{x})\end{align}
\begin{align}=t^3-3\cdot \frac{t^2-1}{2}\cdot t=\frac{2t^3-3t^3+3t}{2}\end{align}
\begin{align}=\frac{-t^3+3t}{2}~~~~\cdots \fbox{答}\end{align}
\(y\) を \(t\) で表す
\begin{align}y=\frac{-t^3+3t}{2}+3\cdot \frac{t^2-1}{2}-2t-1\end{align}
\begin{align}=\frac{-t^3+3t+3t^2-3-6t-3}{2}\end{align}
\begin{align}y=-\frac{1}{2}t^3+\frac{3}{2}t^2-\frac{1}{2}t-\frac{5}{2}~~~~\cdots \fbox{答}\end{align}
ア:2 イ:1 ウ:2 エ:3 オ:3 カ:2 キ:1
(2) の解答〜三角関数の合成〜
\begin{align}t=\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)\end{align}
\(\displaystyle \frac{\pi}{4}\leqq x+\frac{\pi}{4}\leqq \frac{9\pi}{4}\) より\(,\)
\begin{align}-1\leqq \sin\left(x+\frac{\pi}{4}\right)\leqq 1\end{align}
\begin{align}-\sqrt{2}\leqq t \leqq \sqrt{2}~~~~\cdots \fbox{答}\end{align}
ソ:2 タ:2
(3) の解答〜次数下げを利用して計算量を減らす〜
\begin{align}f(t)=-\frac{1}{2}t^3+\frac{3}{2}t^2-\frac{1}{2}t-\frac{5}{2}~(-\sqrt{2}\leqq t \leqq \sqrt{2})\end{align}
とおく.
\begin{align}f^{\prime}(t)=-\frac{3}{2}t^2+3t-\frac{1}{2}=-\frac{1}{2}(3t^2-6t+1)\end{align}
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline t & -\sqrt{2} & \cdots & \displaystyle \frac{3-\sqrt{6}}{3} & \cdots & \sqrt{2} \\ \hline f^{\prime}(t) & {} & – & 0 & + & {} \\ \hline f(t) & \displaystyle \frac{1}{2}+\frac{3}{2}\sqrt{2} & \searrow & \displaystyle f\left(\frac{3-\sqrt{6}}{3}\right) & \nearrow & \displaystyle \frac{1}{2}-\frac{3}{2}\sqrt{2}\\ \hline \end{array}\end{align}
quandle
増減表から \(t=-\sqrt{2}\) のときに最大値を取ることが分かります. 問題は最小値ですが\(,\) \(\displaystyle t=\frac{3-\sqrt{6}}{3}\) を \(3\) 次式である \(f(t)\) に代入するのは明らかに大変ですね. \(f(t)\) を \(f^{\prime}(t)\) で割ることで \(1\) 次式に次数を下げることができます.
ここで \(f(t)\) を \(3t^2-6t+1(=-2f^{\prime}(t))\) で割ると以下の式を得る.
\begin{align}f(t)=(3t^2-6t+1)\left(-\frac{1}{6}t+\frac{1}{6}\right)+\frac{2}{3}t-\frac{8}{3}\end{align}
\(\displaystyle t=\frac{3-\sqrt{6}}{3}\) は \(3t^2-6t+1=0\) の解であるから\(,\)
\begin{align}f\left(\frac{3-\sqrt{6}}{3}\right)=\frac{2}{3}\cdot \frac{3-\sqrt{6}}{3}-\frac{8}{3}\end{align}
\begin{align}=\frac{6-2\sqrt{6}-24}{9}=-2-\frac{2}{9}\sqrt{6}\end{align}
よって\(,\) \(y\) のとり得る範囲は\(,\)
\begin{align}-2-\frac{2}{9}\sqrt{6}\leqq y \leqq \frac{1}{2}+\frac{3}{2}\sqrt{2}~~~~\cdots \fbox{答}\end{align}
チ:2 ツ:2 テ:9 ト:6 ナ:1 ニ:3 ヌ:2
(4) の解答〜三角方程式を解く〜
\begin{align}f(t)=-\frac{1}{2}(t+1)(t^2-4t+5)\end{align}
\(t^2-4t+5=(t-2)^2+1>0\) より\(,\) \(f(t)=0\) のとき\(,\)
\begin{align}t=-1\end{align}
\begin{align}\sin\left(x+\frac{\pi}{4}\right)=-\frac{1}{\sqrt{2}}\end{align}
\begin{align}x+\frac{\pi}{4}=\frac{5}{4}\pi ,~\frac{7}{4}\pi\end{align}
\begin{align}x=\pi ,~\frac{3}{2}\pi ~~~~\cdots \fbox{答}\end{align}
ネ:3 ノ:2
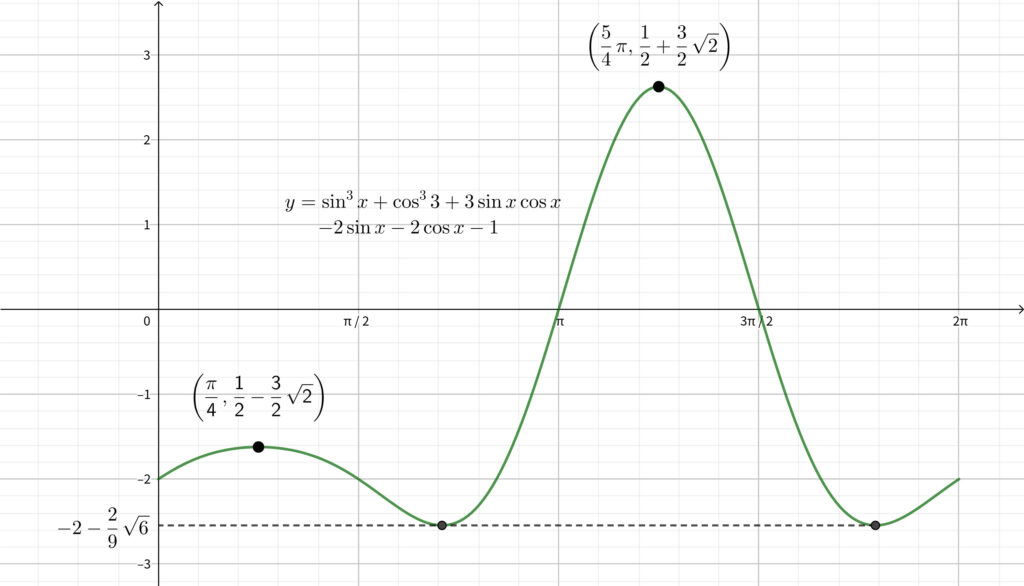
geogebraによる \(y\) のグラフの概形 今回の \(y\) のグラフの概形は以下のようになります.
①最大値をとる \(x\) の値は具体的に計算ができます. \(t=-\sqrt{2}\) の解ですから\(,\)
\begin{align}\sqrt{2}\sin{\left(x+\frac{\pi}{4}\right)}=-\sqrt{2}\end{align}
\begin{align}\sin{\left(x+\frac{\pi}{4}\right)}=-1\end{align}
\begin{align}x+\frac{\pi}{4}=\frac{3\pi}{2}\end{align}
\begin{align}x=\frac{5\pi}{4}\end{align}
②最小値 \(\displaystyle -2-\frac{2}{9}\sqrt{6}\) をとる \(x\) の値は \(2\) つあります.
具体的には\(,\) \(\displaystyle t=\frac{3-\sqrt{6}}{3}\) を解いて得られます.
逆三角関数を用いて表記すると\(,\) \(\displaystyle x=\sin^{-1}\left(\frac{1}{\sqrt{2}}-\frac{\sqrt{3}}{3}\right)-\frac{\pi}{4}\) です. 三角比の表を参照したところ\(,\) 約 \(121°\) と約 \(329°\) です.
② (4) で求めたように \(y=0\) のときの \(x\) の値は \(\displaystyle x=\pi,~\frac{3}{2}\pi\) になっていることがグラフからもわかります.





コメント