公立諏訪東京理科大学 中期 2022年第2問の問題文全文
\begin{align}f(x)=\frac{2x-\sin{2x}}{x^2}~(0<x\leqq \pi )\end{align}
\begin{align}g(x)=\sin{x}-x\cos{x}~(0<x \leqq \pi )\end{align}
で関数 \(f(x),~g(x)\) を定めるとき\(,\) 以下の問いに答えよ.
(1) 導関数 \(g^{\prime}(x)\) を求めよ.
(2) \(0<x \leqq \pi \) における関数 \(y=g(x)\) の最大値を求めよ.
(3) 導関数 \(f^{\prime}(x)\) を \(x,~\sin{x},~\cos{x}\) を用いて表せ.
(4) 導関数 \(f^{\prime}(x)\) を \(x,~\cos{x},~g(x)\) を用いて表せ.
(5) \(0<x \leqq \pi \) における関数 \(y=f(x)\) の最大値を求めよ.
(1) の解答〜積の微分〜
\begin{align}g^{\prime}(x)=\cos{x}-\{1\cdot \cos{x}+x(-\sin{x})\}\end{align}
\begin{align}=x\sin{x}~~~~\cdots \fbox{答}\end{align}
(2) の解答〜導関数の符号を調べる〜
\(0<x\leqq \pi\) より\(,\)
\begin{align}g^{\prime}(x)=x\sin{x}\geqq 0\end{align}
であるから\(,\) \(g(x)\) は \(0<x\leqq \pi\) において単調増加. よって最大値は\(,\)
\begin{align}g(\pi)=\sin{\pi}-{\pi}\cos{\pi}=\pi ~~~~\cdots{答}\end{align}
(3) の解答〜商の微分〜
\begin{align}f^{\prime}(x)=\frac{(2-2\cos{2x})x^2-(2x-\sin{2x})\cdot 2x}{x^4}\end{align}
\begin{align}=\frac{2x-2x\cos{2x}-4x+2\sin{2x}}{x^3}\end{align}
\begin{align}=\frac{-2x(1+\cos{2x})+2\sin{2x}}{x^3}\end{align}
\begin{align}=\frac{-2x\cdot 2\cos^2{x}+4\sin{x}\cos{x}}{x^3}\end{align}
\begin{align}=\frac{4\cos{x}(\sin{x}-x\cos{x})}{x^3}~~~~\cdots \fbox{答}\end{align}
(4) の解答〜(3) ができていればサービス問題〜
\begin{align}f^{\prime}(x)=\frac{4g(x)\cos{x}}{x^3}~~~~\cdots \fbox{答}\end{align}
(5) の解答〜 \(g(x)\) の増減から \(f(x)\) の増減を判断〜
(2) より\(,\) \(g(x)\) は \(0<x\leqq \pi\) において単調増加であり\(,\) \(g(0)=0\) であるから\(,\) \(g(x)>0\) である. よって\(,\) \(0<x\leqq \pi\) において\(,\)
\begin{align}\frac{4g(x)}{x^3}>0\end{align}
であるから\(,\) \(f^{\prime}(x)\) の符号と \(\cos{x}\) の符号は一致する.
よって\(,\) \(f(x)\) の増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline x & (0) & \cdots & \displaystyle \frac{\pi}{2} & \cdots & \pi \\ \hline f^{\prime}(x) & {} & + & 0 & – & {} \\ \hline f(x) & {} & \nearrow & 極大 & \searrow & {} \\ \hline \end{array}\end{align}
増減表より\(,\) 最大値は\(,\)
\begin{align}f\left(\frac{\pi}{2}\right)=2\cdot \frac{\pi}{2}\cdot \frac{4}{{\pi}^2}=\frac{4}{\pi}~~~~\cdots \fbox{答}\end{align}
補足〜 \(y=f(x)\) のグラフの概形〜
\(y=f(x)\) のグラフの概形は以下のようになります.
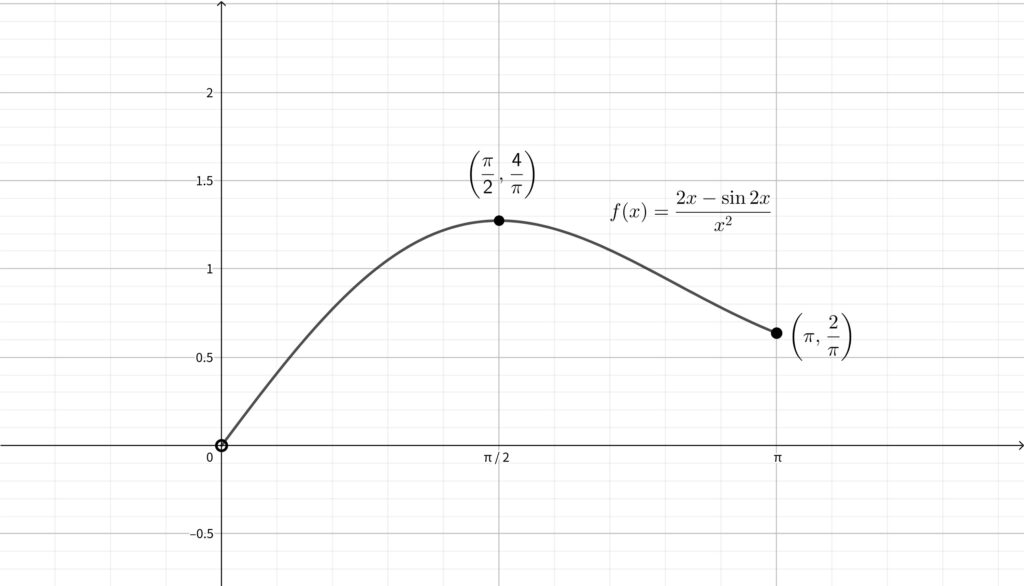
なお\(,\) 今回は最大値さえわかれば良いので不要ですが\(,\)
\begin{align}\lim_{x\to +0}f(x)=0\end{align}
となります. これはそんなに易しくはありません.
ちゃんとやろうと思えば不等式を作ってはさみうちの原理で求めることができます .
実践的にはロピタルの定理を用いることで簡単に極限を求めることができます.
最後に \(\displaystyle \lim_{x\to +0}f(x)=0\) についてまとめておきます.
補足〜 \(\displaystyle \lim_{x\to +0}f(x)\) を求める〜
方法1〜高校数学の範囲で求める(はさみうち)〜
結論から先にいうと\(,\) \(x>0\) において\(,\) 以下の不等式が成り立ちます.
\begin{align}0<\frac{2x-\sin{2x}}{x^2}<\frac{4}{3}x~~~~\cdots (★)\end{align}
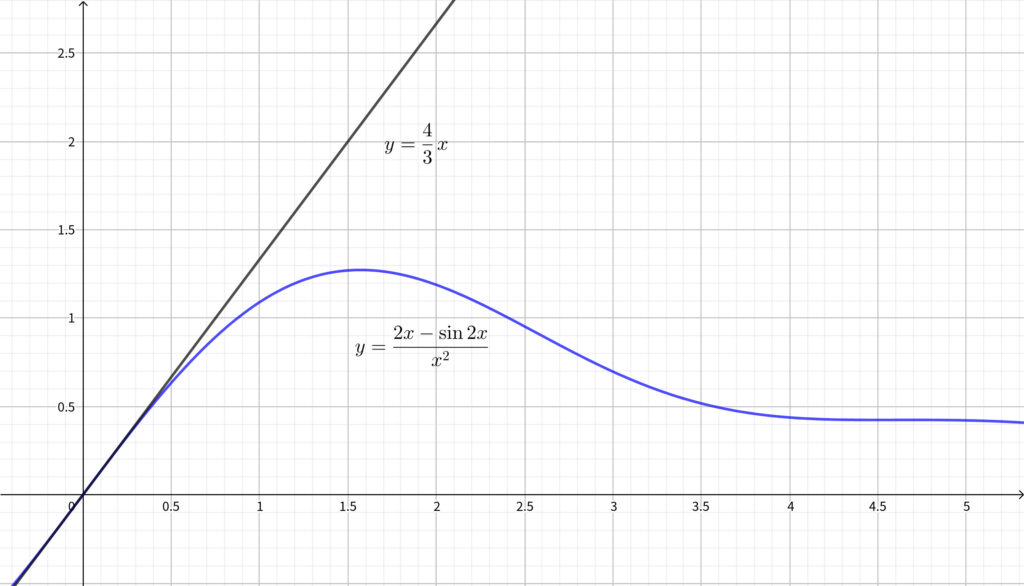
グラフで見ても★が成り立ちそうなのがわかります
\begin{align}\lim_{x\to +0}\frac{4}{3}x=0\end{align}
ですから\(,\) はさみうちの原理により\(,\)
\begin{align}\lim_{x\to +0}f(x)=0\end{align}
となります.
(★) を示すために \(2\) つの不等式を示す必要があります.
\begin{align}①~2x-\sin{2x}>0\end{align}
\begin{align}②~\sin{2x}<2x-\frac{4}{3}x^3\end{align}
① \(2x-\sin{2x}>0\) の証明
\begin{align}h_1(x)=2x-\sin{2x}\end{align}
とおく. \(x>0\) において\(,\)
\begin{align}{h_1}^{\prime}(x)=2-2\cos{2x}\end{align}
\begin{align}=2(1-\cos{2x})=4\sin^2{x}\geqq 0\end{align}
より\(,\) \(h_1(x)\) は \(x>0\) において単調増加. また\(,\) \(h_1(0)=0\) であるから\(,\)\(x>0\) において\(,\)
\begin{align}h_1(x)>0\end{align}
よって\(,\) ①は示された.
② \(\displaystyle \sin{2x}>2x-\frac{4}{3}x^3\) の証明
\begin{align}h_2(x)=\sin{2x}-\left(2x-\frac{4}{3}x^3\right)\end{align}
とおく. \(x>0\) において\(,\)
\begin{align}{h_2}^{\prime}(x)=2\cos{2x}-2+4x^2\end{align}

quandle
\(\cos{2x}\) と \(x^2\) が混在していて\(,\) \({h_2}^{\prime}(x)=0\) を解くことができず\(,\) \({h_2}^{\prime}(x)\) の符号を直ちに判断することが難しいです. こういうときは\(,\) もう \(1\) 回微分をすることで\(,\) \({h_2}^{\prime}(x)\) のグラフの増減を調べてみることが必要です.
\begin{align}{h_2}^{\prime \prime}(x)=-4\sin{2x}+8x\end{align}

quandle
これも \(\sin{2x}\) と \(x\) が混在しているので\(,\) もう \(1\) 回微分してみます.
\begin{align}{h_2}^{\prime \prime \prime}(x)=-8\cos{2x}+8\end{align}
\begin{align}=8(1-\cos{2x})=16\sin^2{x}>0\end{align}
よって\(,\) \({h_2}^{\prime \prime}(x)\) は \(x>0\) で単調増加\(,\) かつ \({h_2}^{\prime \prime}(0)=0\) であるから\(,\)
\begin{align}{h_2}^{\prime \prime}(x)>0\end{align}
ゆえに\(,\) \({h_2}^{\prime}(x)\) は \(x>0\) で単調増加\(,\) かつ \({h_2}^{\prime}(0)=2-2=0\) であるから\(,\)
\begin{align}{h_2}^{\prime}(x)>0\end{align}
したがって\(,\) \(h_2(x)\) は \(x>0\) で単調増加\(,\) かつ \(h_2(0)=0\) であるから\(,\)
\begin{align}h_2(x)>0\end{align}
以上より\(,\) ② は示された.
方法2〜ロピタルの定理を利用する〜
ロピタルの定理を適用することで極限値を出すことができます. 厳密には適用条件は複雑ですが\(,\) 今回は検算できるレベルで十分(そもそも極限を求める必要のない問題ですので)なので\(,\) 以下の大雑把な形でロピタルの定理を紹介して適用するにとどめます.
ロピタルの定理(超大雑把ver.)
微分可能な関数 \(f(x),~g(x)\) に対して\(,\) \(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}\) が \(\displaystyle \frac{0}{0}~\mathrm{or}~\frac{\infty}{\infty}\) の形の不定形であるとき\(,\)
\begin{align}\lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}\frac{f^{\prime}(x)}{g^{\prime}(x)}\end{align}
※ \(a\) は \(\pm \infty\) であっても成り立ちます.
ロピタルの定理より\(,\)
\begin{align}\lim_{x\to +0}\frac{2x-\sin{2x}}{x^2}=\lim_{x\to +0}\frac{2-2\cos{2x}}{2x}\end{align}
\begin{align}=\lim_{x\to +0}\frac{1-\cos{2x}}{x}=\lim_{x\to +0}\frac{2\sin^2{x}}{x}\end{align}
\begin{align}=\lim_{x\to +0}2\cdot \frac{\sin{x}}{x}\cdot \sin{x}=2\cdot 1\cdot 0=0\end{align}





2022年第3問-2.jpg)
2022年第3問-1-120x68.jpg)
2022年第3問-3-120x68.jpg)
コメント