山口東京理科大学 薬学部中期 2022年第5問の問題文全文
\(2\) つの関数 \(f(x)=x^3+3x^2+3x\) と \(g(x)=a^2x+b\) ( \(a\) と \(b\) は実数) を考える. このとき\(,\) 次の (1)\(,\) (2) の問題に答えなさい.
(1) \(a=3,~b=8\) のとき\(,\) 曲線 \(y=f(x)\) と直線 \(y=g(x)\) で囲まれた部分の面積を求めなさい.
(2) \(b=-1\) のとき\(,\) 曲線 \(y=f(x)\) と直線 \(y=g(x)\) が \(3\) 点で交わるような \(a\) の範囲を求めなさい.
(1) の解答〜面積は (上の式)ー(下の式)〜
\(a=3,~b=8\) のとき\(,\) \(g(x)=9x+8\) である.
\begin{align}f(x)-g(x)=x^3+3x^2+3x-(9x+8)\end{align}
\begin{align}=x^3+3x^2-6x-8=(x+1)(x+4)(x-2)\end{align}
であるから\(,\) \(y=f(x)\) と \(y=g(x)\) の位置関係は以下の図のようになる.
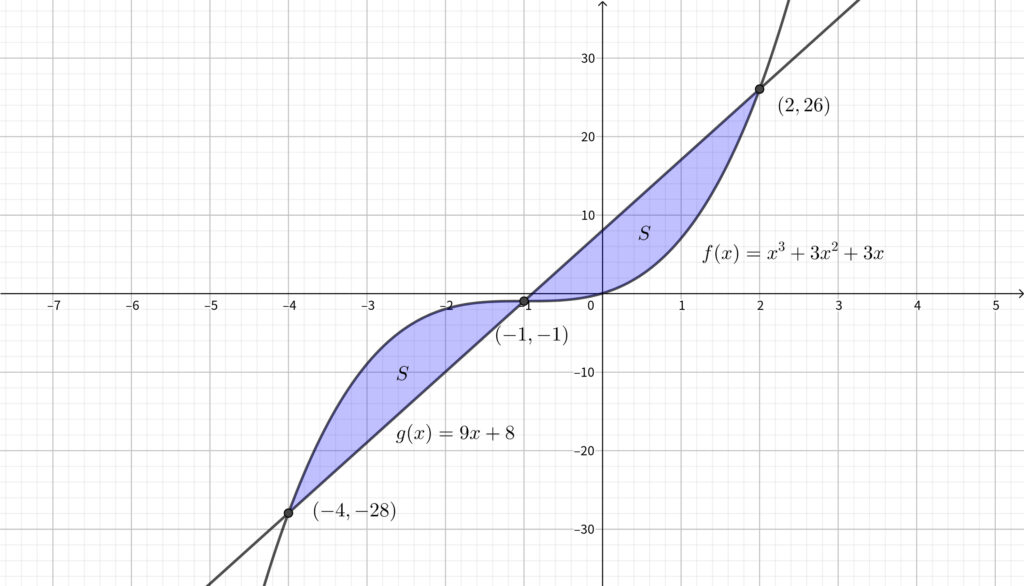
求める面積を \(S\) とおくと\(,\)
\begin{align}S=\int_{-4}^{-1}\{f(x)-g(x)\}dx+\int_{-1}^4\{g(x)-f(x)\}dx\end{align}
である. ここで\(,\)
\begin{align}F(x)=\frac{1}{4}x^4+x^3-3x^2-8x\end{align}
とおくと\(,\) \(F^{\prime}(x)=f(x)-g(x)\) であるから\(,\)
\begin{align}S=\biggl[F(x)\biggr]_{-4}^{-1}-\biggl[F(x)\biggr]_{-1}^2\end{align}
\begin{align}=2F(-1)-F(-4)-F(-2)\end{align}
\begin{align}=2\left(\frac{1}{4}-1-3+8\right)-(64-64-48+32)-(4+8-12-16)\end{align}
\begin{align}=\frac{17}{2}+16+16=\frac{81}{2}~~~~\cdots \fbox{答}\end{align}

quandle
\(F(x)\) とおいて計算することで\(,\) 計算量と記述量をへらすことができるのでおすすめです!
(2) の解答〜「3点で交わる」を「極大値×極小値<0」と読み替える〜
\begin{align}f^{\prime}(x)=3x^2+6x+3=3(x+1)^2\geqq 0\end{align}
であるから \(f(x)\) は単調増加関数である.
\(a=0\) のとき\(,\) \(g(x)=-1\) であり\(,\) \(x\) 軸と平行な直線になるから\(,\) \(y=f(x)\) と \(y=g(x)\) が異なる \(3\) 点で交わることはない. よって\(,\) \(a\neq 0\) としてよい.
曲線 \(y=f(x)\) と直線 \(y=g(x)\) が \(3\) 点で交わるとき\(,\) 方程式
\begin{align}x^3+3x^2+3x=a^2x-1\end{align}
は異なる \(3\) つの実数解を持つ.
\begin{align}h(x)=x^3+3x^2+(3-a^2)x+1\end{align}
とおくと\(,\) \(h(x)=0\) が異なる \(3\) つの実数解をもてばよい. つまり\(,\) \(h(x)\) が極大値と極小値をもち\(,\) その積が負となればよい.
\begin{align}h^{\prime}(x)=3x^2+6x+(3-a^2)\end{align}
であり\(,\) \(h^{\prime}(x)=0\) の判別式を \(D\) とすると\(,\) \(a\neq 0\) より\(,\)
\begin{align}\frac{D}{4}=3^2-3(3-a^2)=3a^2>0\end{align}
であるから\(,\) \(h^{\prime}(x)=0\) は異なる \(2\) つの実数解 \(\alpha ,~\beta~(\alpha <\beta)\) をもつ.
さらに\(,\)
\begin{align}h(x)=\left(\frac{1}{3}x+\frac{1}{3}\right)(3x^2+6x+3-a^2)-\frac{2}{3}a^2x+\frac{1}{3}a^2\end{align}
\begin{align}=\frac{1}{3}(x+1)h^{\prime}(x)-\frac{a^2}{3}(2x-1)\end{align}
であり\(,\) \(h^{\prime}(\alpha )=0,~h^{\prime}(\beta )=0\) より\(,\)
\begin{align}h(\alpha )h(\beta )=-\frac{a^2}{3}(2\alpha -1)\cdot \left\{-\frac{a^2}{3}(2\beta -1)\right\}\end{align}
\(a\neq 0\) より\(,\) \(a^2>0\) であるから\(,\) \(h(\alpha )h(\beta )<0\) のとき\(,\)
\begin{align}(2\alpha -1)(2\beta -1)<0\end{align}
\begin{align}4\alpha \beta -2(\alpha +\beta )+1<0\end{align}
解と係数の関係より\(,\)
\begin{align}\alpha +\beta =-2,~\alpha \beta =\frac{3-a^2}{3}\end{align}
だから\(,\)
\begin{align}\frac{4(3-a^2)}{3}+5<0\end{align}
\begin{align}4a^2-27>0\end{align}
\begin{align}(2a-3\sqrt{3})(2a+3\sqrt{3})>0\end{align}
\(a\neq 0\) より\(,\)
\begin{align}a<-\frac{3\sqrt{3}}{2},~\frac{3\sqrt{3}}{2}<a~~~~\cdots \fbox{答}\end{align}






コメント