理学部第二部2022年第１問の問題文全文
関数 \(f(x)\) を \(f(x)=(x-1)^2(x-2)\) とする.
関数 \(S(t)\) を \(\displaystyle S(t)=\int_t^{t+1}|f(x)|dx~(0\leqq t \leqq 2)\) と定める.
(1) \(f(x)\) の不定積分は\(,\) 部分積分法を用いることにより\(,\)
\begin{align}\int f(x)dx=\frac{~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emイウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}(x-1)^3\left(~\fbox{$\hskip0.4emエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~x-~\fbox{$\hskip0.4em オ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\right)+C\end{align}
のように求められる. ただし\(,\) \(C\) は積分定数である.
また\(,\) \(\displaystyle S(0)=\frac{~\fbox{$\hskip0.4emカ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emキク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\) である.
(2) \(S(t)\) の導関数を \(S^{\prime}(t)\) とおく.
\(0<t<1\) のとき\(,\) \(S^{\prime}(t)=-~\fbox{$\hskip0.4emケ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~t^2+~\fbox{$\hskip0.4emコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~t-~\fbox{$\hskip0.4emサ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である.
\(1<t<2\) のとき\(,\) \(S^{\prime}(t)=~\fbox{$\hskip0.4emシ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~t^3~-\fbox{$\hskip0.4emス\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~t^2+~\fbox{$\hskip0.4emセ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~t-~\fbox{$\hskip0.4emソ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である.
(3) \(t\) が \(0\leqq t \leqq 2\) のとき\(,\) \(S(t)\) は \(\displaystyle t=~\frac{~\fbox{$\hskip0.4emタ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emチ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\) で最小値 \(\displaystyle \frac{~\fbox{$\hskip0.4emツ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{~\fbox{$\hskip0.4emテトナ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\) をとる.
(1) の解答〜部分積分法を利用〜
\begin{align}\int f(x)dx=\int (x-1)^2(x-2)dx\end{align}
\begin{align}=\frac{1}{3}(x-1)^3(x-2)-\int \frac{1}{3}(x-1)^3dx\end{align}
\begin{align}=\frac{1}{3}(x-1)^3(x-2)-\frac{1}{12}(x-1)^4+C\end{align}
\begin{align}=\frac{1}{12}(x-1)^3\{4(x-2)-(x-1)\}+C\end{align}
\begin{align}=\frac{1}{12}(x-1)^3(3x-7)+C~~~~\cdots \fbox{答}\end{align}
\begin{align}S(0)=\int_0^1|f(x)|dx=\int_0^1-f(x)dx\end{align}
\begin{align}=\biggl[-\frac{1}{12}(x-1)^3(3x-7)\biggr]_0^1=\frac{7}{12}~~~~\cdots \fbox{答}\end{align}
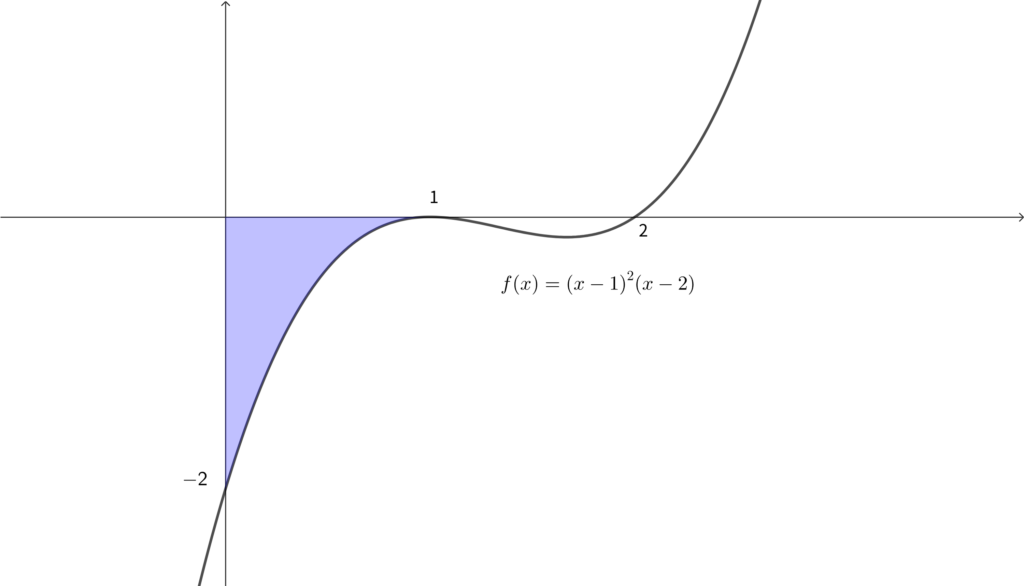\(0\leqq x \leqq 1\) において \(f(x)\) は負の値をとる
ア：１ イ：１ ウ：２ エ：３ オ：７ カ：７ キ：１ ク：２
(1) の別解〜計算だけならこっちの方が楽〜
\begin{align}\int f(x)dx=\int (x-1)^2(x-2)dx\end{align}
\begin{align}=\int (x-1)^2\{(x-1)-1\}dx=\int (x-1)^3dx-\int (x-1)^2dx\end{align}
\begin{align}=\frac{1}{4}(x-1)^4-\frac{1}{3}(x-1)^3+C=\frac{1}{12}(x-1)^3\{3(x-1)-4\}+C\end{align}
\begin{align}=\frac{1}{12}(x-1)^3(3x-7)+C\end{align}
quandle
別解の方が早いし楽ですが\(,\) わざわざ「部分積分を用いて」と誘導があるので素直に従ったほうがいいと思います. 出題者が部分積分をあえて使わせることで何かに気づいてほしいということがあるからです.
(2) の解答〜(1) の結果を使う〜
\(0\leqq t \leqq 1\) のとき\(,\) \(t\leqq x \leqq t+1\) において \(f(x)\) は正の値をとる
\(0\leqq t \leqq 1\) のとき\(,\)
\begin{align}S(t)=\int_t^{t+1}|f(x)|dx=\int_t^{t+1}-f(x)dx\end{align}
\begin{align}=\biggl[-\frac{1}{12}(x-1)^3(3x-7)\biggr]_t^{t+1}\end{align}
\begin{align}=-\frac{1}{12}\left\{t^3(3t-4)-(t-1)^3(3t-7)\right\}=-\frac{1}{12}\left(12t^3-30t^2+24t-7\right)\end{align}
\(0<t<1\) において\(,\)
\begin{align}S^{\prime}(t)=-\frac{1}{12}\left(36t^2-60t+24\right)=-3t^2+5t-2~~~~\cdots \fbox{答}\end{align}
quandle
\(S(t)\) の定義域は \(0\leqq t \leqq 1\) ですが\(,\) \(S^{\prime}(t)\) の定義域は \(0<t<1\) となります. 端点での微分は考慮しないためです.
\(\displaystyle F(x)=\frac{1}{12}(x-1)^3(3x-7)\) とおく.
\(1\leqq t \leqq 2\) のとき\(,\)
\begin{align}S(t)=\int_t^2-f(x)dx+\int_2^{t+1}f(x)dx\end{align}
\begin{align}=\biggl[-F(x)\biggr]_t^2+\biggl[F(x)\biggr]_2^{t+1}=F(t)+F(t+1)-2F(2)\end{align}
\begin{align}=\frac{1}{12}(t-1)^3(3t-7)+\frac{1}{12}t^3(3t-4)-2\cdot \left(-\frac{1}{12}\right)\end{align}
\begin{align}=\frac{1}{12}\left(6t^4-20t^3+30t^2-24t+9\right)\end{align}
\(1<t<2\) において\(,\)
\begin{align}S^{\prime}(t)=\frac{1}{12}\left(24t^3-60t^2+60t-24\right)\end{align}
\begin{align}=2t^3-5t^2+5t-2~~~~\cdots \fbox{答}\end{align}
ケ：３ コ：５ サ：２ シ：２ ス：５ セ：５ ソ：２
(2) の別解〜微分積分学の基本定理（の一般化）の利用〜
積分範囲が定数でない場合は以下の公式が利用できることが多いです.
微分積分学の基本定理（の一般化）
連続関数 \(f(x)\)\(,\) 微分可能な関数 \(g(x),~h(x)\) に対して以下が成り立つ.
\begin{align}\frac{d}{dx}\int_{h(x)}^{g(x)}f(t)dt=f\left(g(x)\right)g^{\prime}(x)-f\left(h(x)\right)h^{\prime}(x)\end{align}
\(0\leqq t \leqq 1\) のとき\(,\)
\begin{align}S(t)=\int_t^{t+1}-f(x)dx\end{align}
\(0<t<1\) において\(,\)
\begin{align}S^{\prime}(t)=-f(t+1)\cdot (t+1)^{\prime}+f(t)\end{align}
\begin{align}=-t^2(t-1)+(t-1)^2(t-2)=(t-1)\{-t^2+(t-1)(t-2)\}\end{align}
\begin{align}=(t-1)(-3t+2)=-3t^2+5t-2~~~~\cdots \fbox{答}\end{align}
\(1\leqq t \leqq 2\) のとき\(,\)
\begin{align}S(t)=\int_t^2-f(x)dx+\int_2^{t+1}f(x)dx\end{align}
\(1<t<2\) において\(,\)
\begin{align}S^{\prime}(t)=f(t)+f(t+1)\cdot (t+1)^{\prime}\end{align}
\begin{align}=(t-1)^2(t-2)+t^2(t-1)=2t^3-5t^2+5t-2~~~~\cdots \fbox{答}\end{align}
(3) の解答〜\(t=1\) で微分可能かを確認〜
\(t=1\) における微分可能性を調べる. \(\displaystyle S(1)=\frac{1}{12}\) であることに注意して\(,\)
\begin{align}\lim_{h\to +0}\frac{S(1+h)-S(1)}{h}\end{align}
\begin{align}=\lim_{h\to +0}\cfrac{\cfrac{1}{12}\{6(1+h)^4-20(1+h)^3+30(1+h)^2-24(1+h)+9\}-\cfrac{1}{12}}{h}\end{align}
\begin{align}=\lim_{h\to +0}\frac{6h^4+4h^3+6h^2}{12h}=\lim_{h\to +0}\left(\frac{1}{2}h^3+\frac{1}{3}h^2+\frac{1}{2}h\right)=0\end{align}
\begin{align}\lim_{h\to -0}\frac{S(1+h)-S(1)}{h}\end{align}
\begin{align}=\lim_{h\to -0}\cfrac{-\cfrac{1}{12}\{12(1+h)^3-30(1+h)^2+24(1+h)-7\}-\cfrac{1}{12}}{h}\end{align}
\begin{align}=\lim_{h\to -0}\frac{12h^3+6h^2}{-12h}=\lim_{h\to -0}\left(-h^2-\frac{1}{2}h\right)=0\end{align}
よって\(,\) \(S(t)\) は \(t=1\) で微分可能であり\(,\) \(S^{\prime}(1)=0\) である.
quandle
今回の問題は穴埋め式なのと\(,\) 最小値さえわかればいいことから\(,\) 実際の試験では微分可能性の議論はスキップします. 記述だとしたらここまで書かないと満点解答にはならないかと思います.
(2) の結果と合わせると\(,\)
\begin{align}S^{\prime}(t)=\left\{\begin{array}{ccc}-(3t-2)(t-1) & (0<t<1) \\ 0 & (t=1) \\ 2t^3-5t^2+5t-2 & (1<t<2) \end{array}\right.\end{align}
ここで\(,\) \(0<t<1\) のとき\(,\) \(-(t-1)>0\) であるから\(,\) \(S^{\prime}(t)\) の符号と\(,\) \(3t-2\) の符号は一致する.
また\(,\) \(1<t<2\) のとき\(,\)
\begin{align}2t^3-5t^2+5t-2=(t-1)(2t^2-3t+2)\end{align}
\begin{align}=(t-1)\left\{2\left(t-\frac{3}{4}\right)^2+\frac{7}{8}\right\}>0\end{align}
あるから\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|}\hline t & 0 & \cdots & \displaystyle \frac{2}{3} & \cdots & 1 & \cdots & 2 \\ \hline S^{\prime}(t) & ✕ & – & 0 & + & 0 & + & ✕ \\ \hline S(t) & \displaystyle \frac{7}{12} & \searrow & \displaystyle \frac{7}{108} & \nearrow & \displaystyle \frac{1}{12} & \nearrow & \displaystyle \frac{17}{12}\\ \hline \end{array}\end{align}
増減表より\(,\)
\begin{align}t=\frac{2}{3}~のとき,~最小値~\frac{7}{108}~をとる~~~~\cdots \fbox{答}\end{align}
タ：２ チ：３ ツ：７ テ：１ ト：０ ナ：８
コメント