東京理科大学先進工学部2023年第2問の問題文全文
\(f(x)=x^3-6x^2+9x+2\) とおく.
(1) \(3\) 次方程式 \(f(x)=4\) の解は\(,\)
\begin{align}x=~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~,~ x=~\fbox{$\hskip0.4emイ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\pm \sqrt{~\fbox{$\hskip0.4emウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である.
(2) \(3\) 次方程式 \(f(x)=k\) が異なる \(2\) 個の実数解をもつような実数 \(k\) の値は\(,\) 小さい順に\(,\)
\begin{align}k=~\fbox{$\hskip0.4emエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~,~\fbox{$\hskip0.4emオ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\end{align}
である.
\(k=~\fbox{$\hskip0.4em エ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) のとき\(,\) 異なる実数解は小さい順に \(x=~\fbox{$\hskip0.4emカ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) \(,\) \(x=~\fbox{$\hskip0.4emキ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である.
\(k=~\fbox{$\hskip0.4em オ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) のとき\(,\) 異なる実数解は小さい順に \(x=~\fbox{$\hskip0.4emク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) \(,\) \(x=~\fbox{$\hskip0.4emケ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である.
(3) \(3\) 次方程式 \(f(x)=k\) が異なる \(3\) つの実数解をもつような実数 \(k\) の値の範囲は\(,\)
\begin{align}\fbox{$\hskip0.4emコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~<k<~\fbox{$\hskip0.4emサ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\end{align}
である.
(1) の解答〜因数定理を用いて因数分解〜
\begin{align}x^3-6x^2+9x+2=4\end{align}
\begin{align}\Leftrightarrow x^3-6x^2+9x-2=0\end{align}
\begin{align}\Leftrightarrow (x-2)(x^2-4x+1)=0\end{align}
\begin{align}\therefore x=2,~2\pm \sqrt{3}~~~~\cdots \fbox{答}\end{align}
ア:2 イ:2 ウ:3
(2) の解答〜 「方程式の解」を「グラフの共有点」と言い換える〜
\begin{align}f^{\prime}(x)=3x^2-12x+9=3(x-1)(x-3)\end{align}
このとき\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline x & \cdots & 1 & \cdots & 3 & \cdots \\ \hline f^{\prime}(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & 6 & \searrow & 2 & \nearrow \\ \hline \end{array}\end{align}
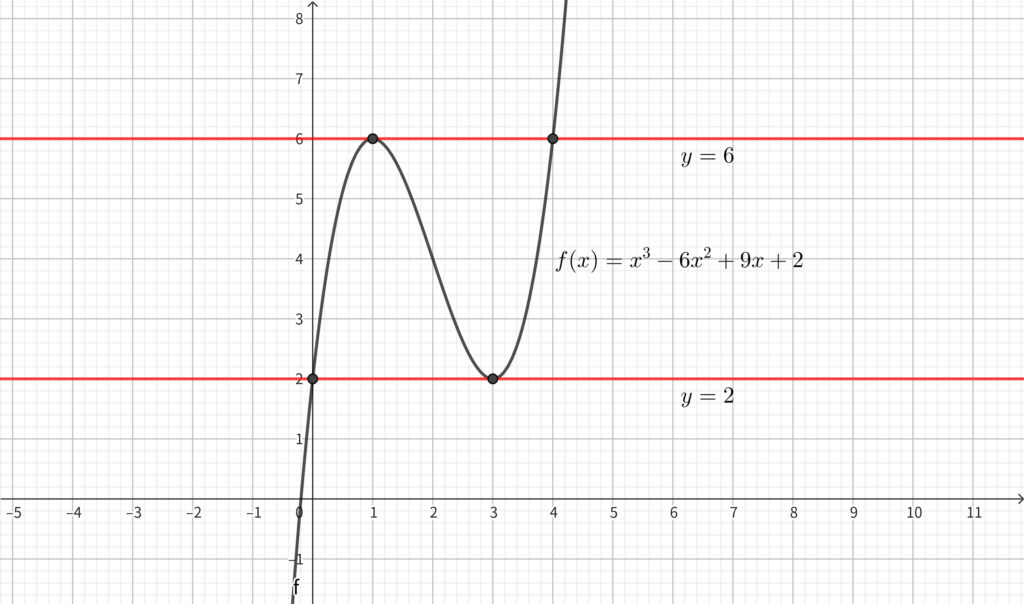
グラフより\(,\) 求める \(k\) の値は小さい順に
\begin{align}k=2,~6~~~~\cdots \fbox{答}\end{align}
\(k=2\) のとき\(,\)
\begin{align}x^3-6x^2+9x=0\end{align}
\begin{align}\Leftrightarrow x(x-3)^2=0\end{align}
\begin{align}\therefore x=0,~3~~~~\cdots \fbox{答}\end{align}
\(k=6\) のとき\(,\)
\begin{align}x^3-6x^2+9x-4=0\end{align}
\begin{align}\Leftrightarrow (x-1)^2(x-4)=0\end{align}
\begin{align}\therefore x=1,~4~~~~\cdots \fbox{答}\end{align}
エ:2 オ:6 カ:0 キ:3 ク:1 ケ:4
(3) の解答〜(2) のグラフを使えば瞬殺〜
(2) のグラフより\(,\)
\begin{align}2<k<6~~~~\cdots \fbox{答}\end{align}
コ:2 サ:6





コメント