C方式・グローバル方式2023年第5問の問題文全文
座標平面上の曲線 \(C\) の方程式を
\begin{align}y=|x^3-3x^2|\end{align}
とする. 曲線 \(C\) 上の点 \((1,~2)\) における接線を \(\ell \) とすると\(,\) \(\ell \) の方程式は
\begin{align}y=~\fbox{$\hskip0.4emア\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~x-~\fbox{$\hskip0.4emイ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\end{align}
であり\(,\) 曲線 \(C\) と \(\ell \) で囲まれた部分の面積を \(S\) とすると
\begin{align}S=-~\fbox{$\hskip0.4emウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~+~\fbox{$\hskip0.4emエ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\sqrt{~\fbox{$\hskip0.4emオ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}\end{align}
である.
\(b\) を実数とし\(,\) 直線 \(m\) の方程式を
\begin{align}y=-x+b\end{align}
とする. 直線 \(m\) が曲線 \(C\) と異なる \(4\) つの共有点をもつとき\(,\) \(b\) の値の範囲は
\begin{align}\fbox{$\hskip0.4emカ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~<b<~\frac{~\fbox{$\hskip0.4emキク\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~+~\fbox{$\hskip0.4emケコ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\sqrt{~\fbox{$\hskip0.4emサ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}~}{\fbox{$\hskip0.4emシ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}\end{align}
である.
\(C\) の概形をかいてみる〜絶対値付き関数のグラフ〜
<確認>絶対値付き関数のグラフのかきかた
絶対値付きの関数のグラフは
中身の関数のグラフをかいて \(x\) 軸より下の部分を折り返す
ことで場合分けせずにかくことが可能です. 詳しくは下のリンクをご参照ください.(「高校数学の美しい物語」さんはブログでの無断使用OKと明記されていますので使用させていただきました.)
https://manabitimes.jp/math/1212
\(C\) の概形
\begin{align}f(x)=x^3-3x^2\end{align}
とおく.
\begin{align}f^{\prime}(x)=3x^2-6x=3x(x-2)\end{align}
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline x & \cdots & 0 & \cdots & 2 & \cdots \\ \hline f^{\prime}(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & 0 & \searrow & -4 & \nearrow \\ \hline \end{array}\end{align}
増減表より\(,\) \(y=|f(x)|\) のグラフの概形は下図のようになる.
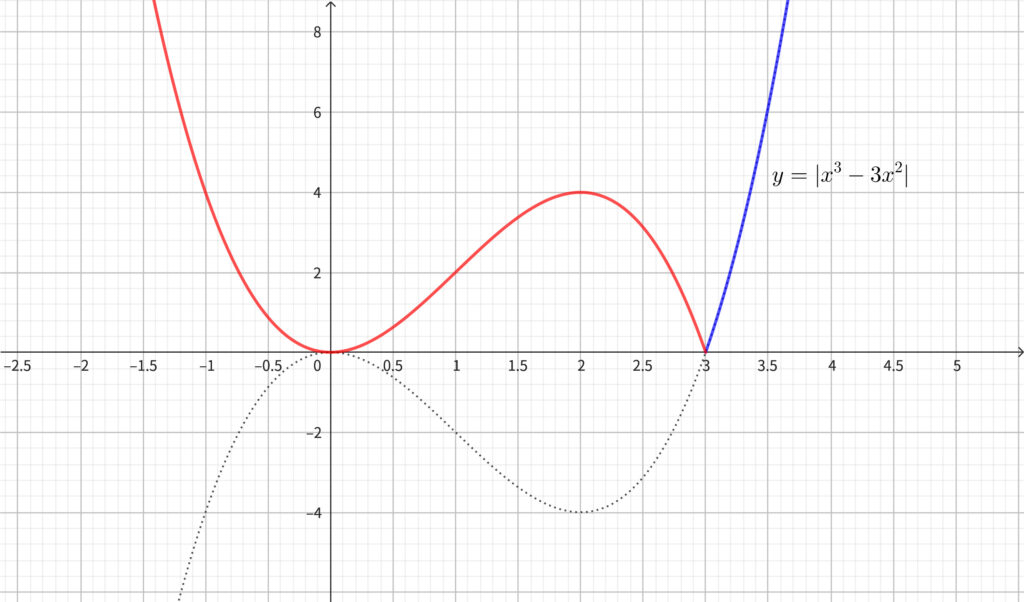
\(\ell \) を求める〜 \(x<3\) のときの導関数を利用〜
\(x<3\) のとき\(,\)
\begin{align}y=-x^3+3x^2,~y^{\prime}=-3x^2+6x\end{align}
であるから\(,\) \(x=1\) のとき\(,\) \(y^{\prime}=3\) である. よって\(,\) \(\ell \) の方程式は\(,\)
\begin{align}\ell ~:~y=3(x-1)+2\end{align}
\begin{align}\therefore \ell ~:~y=3x-1~~~~\cdots \fbox{答}\end{align}
ア:3 イ:1
\(S\) を求める〜グラフの位置関係を正しく把握する〜
\(C\) と \(\ell \) の共有点を求める
\(x\leqq 3\) のとき\(,\)
\begin{align}-x^3+3x^2=3x-1\end{align}
\begin{align}\Leftrightarrow x^3-3x^2+3x-1=0\end{align}
\begin{align}\Leftrightarrow (x-1)^3=0\end{align}
\begin{align}\therefore x=1\end{align}
\(x\geqq 3\) のとき\(,\)
\begin{align}x^3-3x^2=3x-1\end{align}
\begin{align}\Leftrightarrow (x+1)(x^2-4x+1)=0\end{align}
\begin{align}\therefore x=-1,~2\pm \sqrt{3}\end{align}
\(x\geqq 3\) より\(,\)
\begin{align}x=2+\sqrt{3}\end{align}
以上より\(,\) 曲線 \(C\) と 直線 \(\ell \) の位置関係は下図のようになる.
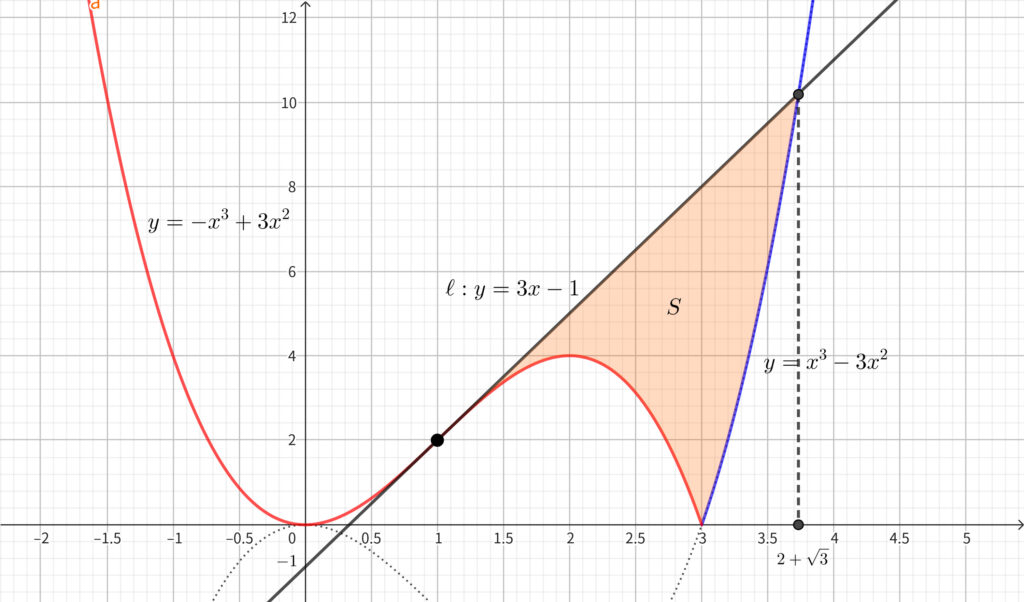

quandle
\(x<3\) において\(,\)
\begin{align}y^{\prime \prime}=-6x+6=-6(x-1)\end{align}
であることから\(,\) \(x=1\) のとき\(,\) \(y^{\prime \prime}=0\) になります.
また\(,\) \(x=1\) の近くで \(y^{\prime \prime}\) の符号が変わるので\(,\)点 \((1,~2)\) は変曲点であることがわかります. 変曲点であることがわかっていれば接線もかきやすいですね.
\(S\) を求める〜\(x=3\) の前後で被積分関数が変わる〜
\begin{align}S=\int_1^3\{(3x-1)-(-x^3+3x^2)\}dx+\int_3^{2+\sqrt{3}}\{(3x-1)-(x^3-3x^2)\}dx\end{align}
\begin{align}=\int_1^3(x-1)^3dx+\int_3^{2+\sqrt{3}}(-x^3+3x^2+3x-1)dx\end{align}
\begin{align}=\biggl[\frac{1}{4}(x-1)^4\biggr]_1^3+\biggl[-\frac{1}{4}x^4+x^3+\frac{3}{2}x^2-x\biggr]_3^{2+\sqrt{3}}\end{align}
\begin{align}=4-\frac{1}{4}\{(2+\sqrt{3})^4-81\}+\{(2+\sqrt{3})^3-27\}+\frac{3}{2}\{(2+\sqrt{3})^2-9\}-\{(2+\sqrt{3})-3\}\end{align}
\begin{align}=4-\frac{1}{4}(16+56\sqrt{3})+(-1+15\sqrt{3})+\frac{3}{2}(-2+4\sqrt{3})-(-1+\sqrt{3})\end{align}
\begin{align}=-3+6\sqrt{3}~~~~\cdots \fbox{答}\end{align}
ウ:3 エ:6 オ:3
\(b\) を求める〜\(3\) 個になるところを調べる〜
\(y=-x+b\) は傾きが \(-1\) で固定で \(y\) 切片 \(b\) が変化することで動きます.
下図の緑色の直線と青色の直線のときに共有点が \(3\) 個になります. 赤色の直線のように青色と緑色の直線の間にあるときに共有点が \(4\) 個になります.
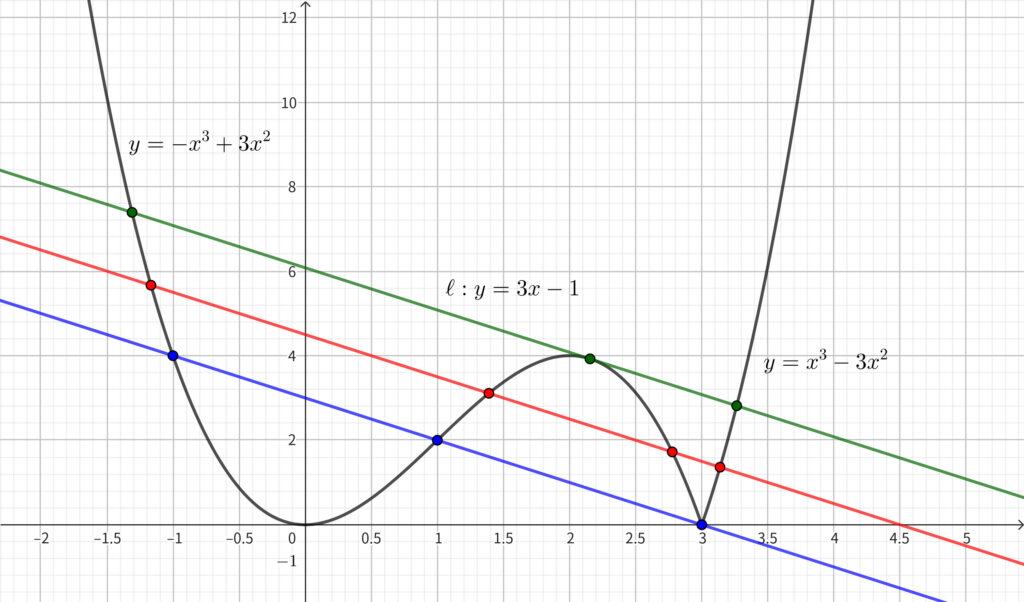
青色の直線の \(y\) 切片を求める
直線 \(y=-x+b\) が点 \((3,~0)\) を通るとき
\begin{align}0=-3+b\end{align}
\begin{align}\therefore b=3\end{align}
緑色の直線の \(y\) 切片を求める
曲線 \(C\) と \(2<x<3\) の範囲で接するときを考える.
\(2<x<3\) における導関数は \(y^{\prime}=-3x^2+6x\) であるから\(,\) \(y^{\prime}=-1\) のとき\(,\)
\begin{align}-3x^2+6x=-1\end{align}
\begin{align}3x^2-6x-1=0\end{align}
\begin{align}\therefore x=\frac{3\pm 2\sqrt{3}}{3}\end{align}
\(2<x<3\) より\(,\)
\begin{align}x=\frac{3+2\sqrt{3}}{3}\end{align}
ここで\(,\) \(g(x)=-x^3+3x^2\) とおくと\(,\)
\begin{align}g(x)=\left(-\frac{1}{3}x+\frac{1}{3}\right)(3x^2-6x-1)+\frac{5}{3}x+\frac{1}{3}\end{align}
より\(,\)
\begin{align}g\left(\frac{3+2\sqrt{3}}{3}\right)=\frac{5}{3}\cdot \frac{3+2\sqrt{3}}{3}+\frac{1}{3}\end{align}
\begin{align}=\frac{18+10\sqrt{3}}{9}\end{align}
よって\(,\) 接点の座標は
\begin{align}\left(\frac{3+2\sqrt{3}}{3},~\frac{18+10\sqrt{3}}{9}\right)\end{align}
であるから\(,\) \(y=-x+b\) が接点を通るとき\(,\)
\begin{align}\frac{18+10\sqrt{3}}{9}=-\frac{3+2\sqrt{3}}{3}+b\end{align}
\begin{align}\therefore b=\frac{27+16\sqrt{3}}{9}\end{align}
よって\(,\) 求める \(b\) の範囲は
\begin{align}3<b<\frac{27+16\sqrt{3}}{9}~~~~\cdots \fbox{答}\end{align}
カ:3 キ:2 ク:7 ケ:1 コ:6 サ:3 シ:9









コメント