山口東京理科大学 前期(共通)2023年第3問(1)の問題文全文
実数 \(x\) の関数 \(f(x)=|x^2-3x-4|\) とする. このとき\(,\)
\begin{align}\int_0^5f(x)dx=\frac{~\fbox{$\hskip0.4emアイ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~}{\fbox{$\hskip0.4emウ\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}}\end{align}
である.
解答〜絶対値を適切に外す〜
\(g(x)=x^2-3x-4\) とおき\(,\) \(g(x)\) の原始関数のうち\(,\) 定数項が \(0\) のものを \(G(x)\) とおく.
\begin{align}G(x)=\frac{1}{3}x^3-\frac{3}{2}x^2-4x\end{align}
\(g(x)=(x+1)(x-4)\) より\(,\)
\begin{align}f(x)=\left\{\begin{array}{cc}-g(x) & (0\leqq x \leqq 4) \\ g(x) & (4\leqq x \leqq 5)\end{array}\right. \end{align}
\begin{align}\int_0^5f(x)dx=\int_0^4-g(x)dx+\int_4^5g(x)dx\end{align}
\begin{align}=\biggl[-G(x)\biggr]_0^4+\biggl[G(x)\biggr]_4^5\end{align}
\begin{align}=\{-G(4)+G(0)\}+\{G(5)-G(4)\}=G(5)-2G(4)+G(0)\end{align}
ここで\(,\)
\begin{align}G(5)=\frac{1}{3}\cdot 125-\frac{3}{2}\cdot 25-20=\frac{250-225-120}{6}=-\frac{95}{6}\end{align}
\begin{align}G(4)=\frac{1}{3}\cdot 64-\frac{3}{2}\cdot 16-16=\frac{64-120}{3}=-\frac{56}{3}\end{align}
\begin{align}G(0)=0\end{align}
であるから\(,\)
\begin{align}\int_0^5f(x)dx=-\frac{95}{6}-2\left(-\frac{56}{3}\right)\end{align}
\begin{align}=\frac{-95+224}{6}=\frac{129}{6}=\frac{43}{2}~~~~\cdots \fbox{答}\end{align}
ア:4 イ:3 ウ:2
補足〜グラフと求めた面積〜
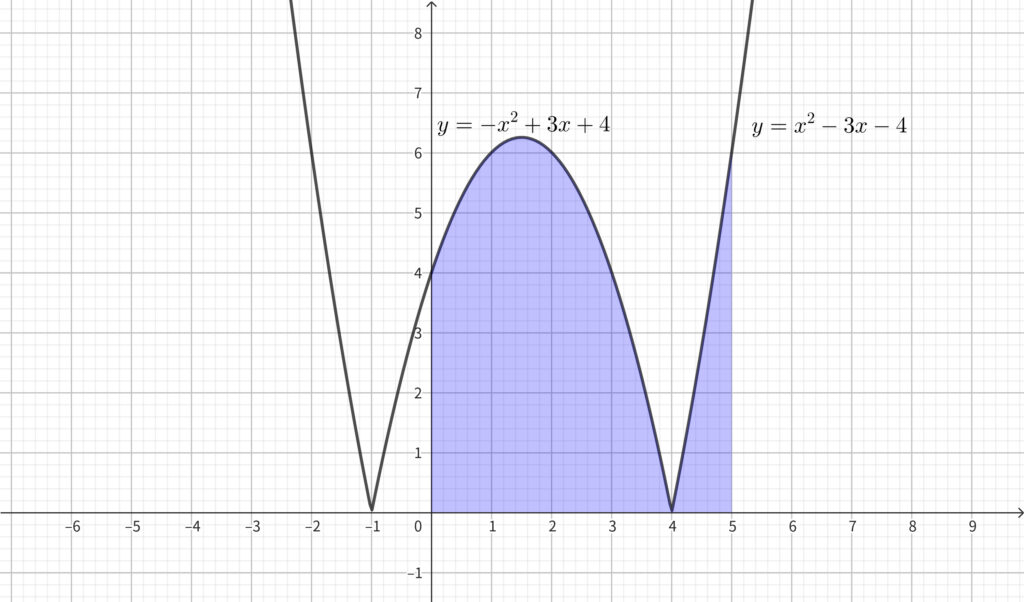
今回の問題で求めた積分の値は以下の図の青色部分の面積である.




コメント