理学部(共通問題)第2問の問題文全文
実数 \(a\) に対して\(,\) \(f(x,~y)=x^3+y^3-a\) とおき\(,\) \(g(x,~y)=x^2+y^2-1\) とおく. 以下の問いに答えよ.
(1) 実数 \(x,~y\) が \(g(x,~y)=0\) を満たすとき\(,\) \(x+y\) のとり得る値の範囲を求めよ. また\(,\) \(g(x,~y)=0\) を満たす正の実数 \(x,~y\) に対する \(x+y\) のとり得る値の範囲も求めよ.
(2) \(t=x+y,~u=xy\) とするとき\(,\) \(x^3+y^3\) を \(t\) と \(u\) の多項式として表わせ. さらに\(,\) \(x,~y\) が \(g(x,~y)=0\) を満たすとき\(,\) \(x^3+y^3\) を \(t\) のみの多項式として表わせ.
(3) \(f(x,~y)=0\) と \(g(x,~y)=0\) を共に満たすような実数 \(x,~y\) が存在するような \(a\) の値の範囲を求めよ.
(4) \(f(x,~y)=0\) と \(g(x,~y)=0\) を共に満たすような正の実数 \(x,~y\) が存在するような \(a\) の値の範囲を求めよ.
(5) \(f(x,~y)=0\) と \(g(x,~y)=0\) を共に満たすような正の実数 \(x,~y\) がただ \(1\) 組だけ存在するような \(a\) の値を求めよ. また\(,\) そのときの \(x,~y\) の値も求めよ.
(1) の解答〜\(2\) つの解法〜
<推奨>解法①〜線形計画法による解答〜
\begin{align}x+y=k\end{align}
とおくと\(,\)
\begin{align}y=-x+k\end{align}
となる. 実数 \(x,~y\) が \(x^2+y^2=1\) を満たすときの \(y\) 切片の最大値・最小値を求めればよい.
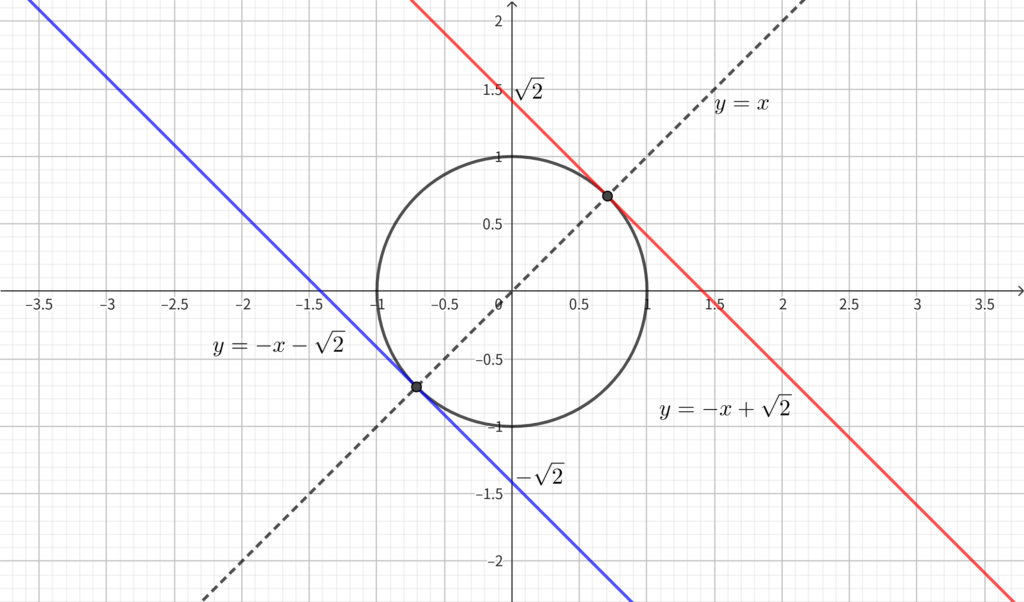
上図の赤い直線のとき \(y\) 切片が最大\(,\) 青い直線のとき \(y\) 切片が最小になる. これらの直線は円 \(x^2+y^2=1\) の接線であるから\(,\) \(x+y-k=0\) と原点との距離が \(1\) である.
\begin{align}\frac{|-k|}{\sqrt{1^2+1^2}}=1\end{align}
\begin{align}k=\pm \sqrt{2}\end{align}
よって\(,\) 求める範囲は\(,\)
\begin{align}-\sqrt{2}\leqq x+y \leqq \sqrt{2}~~~~\cdots \fbox{答}\end{align}
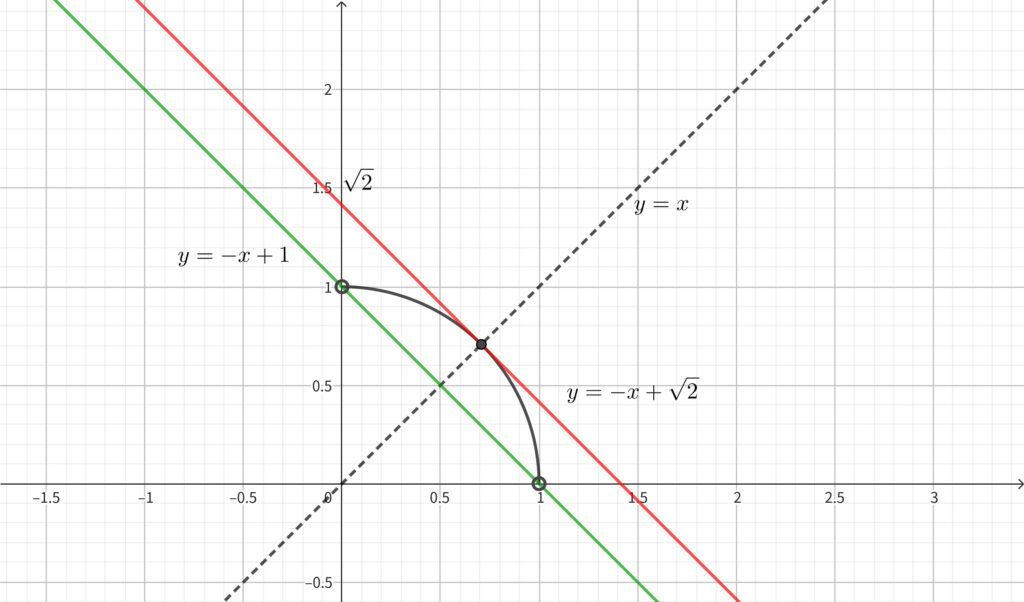
正の実数 \(x,~y\) に制限すると上図のようになる. 緑の直線のとき \(y\) 切片が最小となる. よって\(,\) 求める範囲は
\begin{align}1<x+y \leqq \sqrt{2}~~~~\cdots \fbox{答}\end{align}
解法②〜解の配置問題に帰着〜
\begin{align}x+y=k\end{align}
とおくと\(,\)
\begin{align}y=-x+k\end{align}
であるから\(,\) \(x^2+y^2-1=0\) に代入すると\(,\)
\begin{align}x^2+(-x+k)^2-1=0\end{align}
\begin{align}2x^2-2kx+k^2-1=0\end{align}
となる. この \(2\) 次方程式が実数解をもてばよい. 判別式を \(D\) とおくと\(,\) \(D\geqq 0\) より\(,\)
\begin{align}\frac{D}{4}=(-k)^2-2(k^2-1)\geqq 0\end{align}
\begin{align}(k+\sqrt{2})(k-\sqrt{2})\leqq 0\end{align}
\begin{align}\therefore -\sqrt{2}\leqq x+y \leqq \sqrt{2}~~~~\cdots \fbox{答}\end{align}
正の実数 \(x,~y\) に制限したときは\(,\) 上記の \(2\) 次方程式が正の実数解をもてばよい.
\begin{align}F(x)=2x^2-2kx+k^2-1=2\left(x-\frac{k}{2}\right)^2+\frac{k^2}{2}-1\end{align}
とおく.
\begin{align}\left\{\begin{array}{cc} \displaystyle \frac{k}{2} >0 & \cdots ①\\ D\geqq 0 & \cdots ②\\ f(0)>0 & \cdots ③\end{array}\right.\end{align}
①より\(,\)
\begin{align}k>0\end{align}
②より\(,\)
\begin{align}-\sqrt{2}\leqq k \leqq \sqrt{2}\end{align}
③より\(,\)
\begin{align}f(0)=k^2-1>0\end{align}
\begin{align}(k+1)(k-1)>0\end{align}
\begin{align}\therefore k<-1,~1<k\end{align}
以上より\(,\)
\begin{align}1<x+y\leqq \sqrt{2}~~~~\cdots \fbox{答}\end{align}

quandle
解の配置問題では\(,\) 軸の位置\(,\) 判別式の符号\(,\) 定義域の境界での符号の \(3\) つを調べるのがセオリーです.
(2) の解答〜対称式の変形〜
\begin{align}x^3+y^3=(x+y)^3-3xy(x+y)\end{align}
\begin{align}=t^3-3ut~~~~\cdots \fbox{答}\end{align}
\begin{align}(x+y)^2-2xy=1\end{align}
\begin{align}t^2-2u=1\end{align}
\begin{align}u=\frac{1}{2}t^2-\frac{1}{2}\end{align}
\begin{align}x^3+y^3=t^3-3\left(\frac{1}{2}t^2-\frac{1}{2}\right)t\end{align}
\begin{align}=-\frac{1}{2}t^3+\frac{3}{2}t~~~~\cdots \fbox{答}\end{align}
(3) の解答〜定数分離〜
(1)\(,\) (2) より\(,\)
\begin{align}-\frac{1}{2}t^3+\frac{3}{2}t=a\end{align}
が \(\sqrt{2}\leqq t \leqq \sqrt{2}\) において\(,\) 実数解をもつような \(a\) の値の範囲を求めればよい.
\begin{align}G(t)=-\frac{1}{2}t^3+\frac{3}{2}t\end{align}
とおく.
\begin{align}G^{\prime}(t)=-\frac{3}{2}t^2+\frac{3}{2}=-\frac{3}{2}(t+1)(t-1)\end{align}
より\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|}\hline t & -\sqrt{2} & \cdots & -1 & \cdots & 1 & \cdots & \sqrt{2} \\ \hline G^{\prime}(t) & {} & – & 0 & + & 0 & – & {} \\ \hline G(t) & \displaystyle \frac{\sqrt{2}}{2} & \searrow & -1 & \nearrow & 1 & \searrow & \displaystyle \frac{\sqrt{2}}{2} \\ \hline \end{array}\end{align}
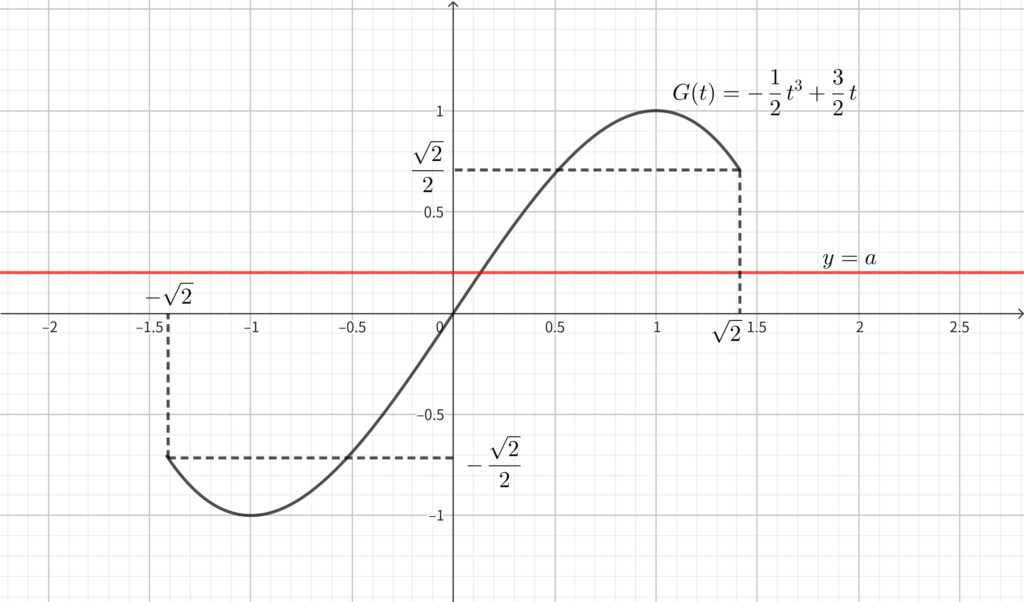
\(y=G(t)\) のグラフは上図のようになり\(,\) これが直線 \(y=a\) と共有点をもてばよいので\(,\)
\begin{align}-1\leqq a \leqq 1~~~~\cdots \fbox{答}\end{align}
(4) の解答〜(3) から即答できる〜
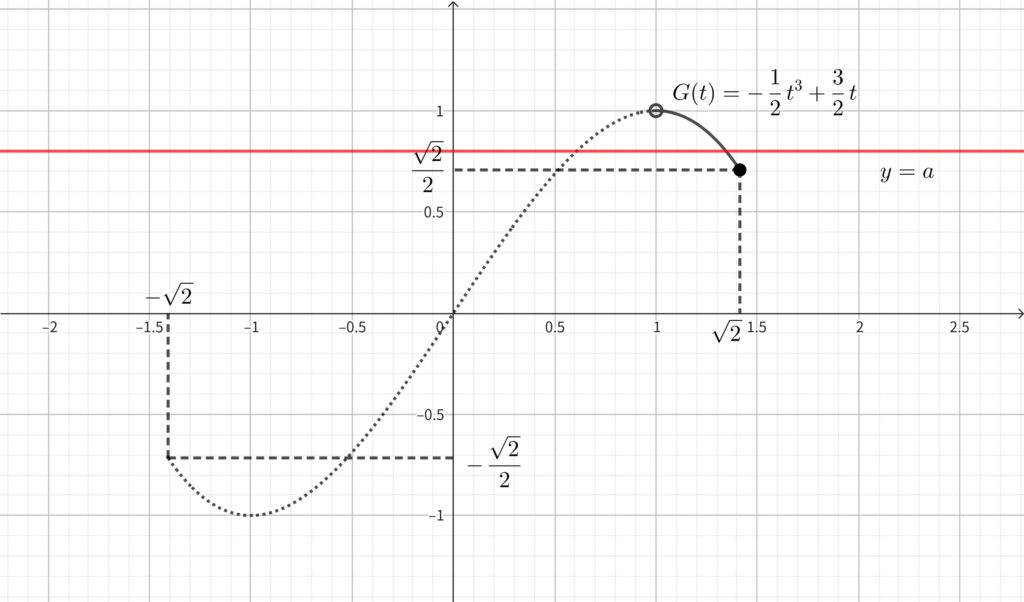
(1)\(,\) (2)\(,\) (3) より\(,\) \(y=G(t)\) のグラフと直線 \(y=a\) が \(1<t\leqq \sqrt{2}\) において\(,\) 共有点をもてばよいので\(,\) (3) のグラフより直ちに
\begin{align}\frac{\sqrt{2}}{2}\leqq a <1~~~~\cdots \fbox{答}\end{align}
とわかる.
(5) の解答〜流れを理解すれば即答できる〜
(1) の図より \(g(x,~y)=0\) を満たす 正の実数 \(x,~y\) は \(,\) \(1<t<\sqrt{2}\) のとき\(,\) \(2\) 組あり\(,\) \(t=\sqrt{2}\) のとき\(,\) \(1\) 組だけ存在する.
(4) より\(,\) \(f(x,~y)=0\) と \(g(x,~y)=0\) を同時に満たす正の実数 \(x,~y\) は \(1<t\leqq \sqrt{2}\) において\(,\) \(\displaystyle \frac{\sqrt{2}}{2}\leqq a<1\) のときに限り\(,\) ただ \(1\) 組存在する.
まとめると\(,\) \(f(x,~y)=0\) と \(g(x,~y)=0\) を満たす正の実数 \(x,~y\) は \(t=\sqrt{2}\)\(,\) つまり \(\displaystyle a=\frac{\sqrt{2}}{2}\) のとき\(,\) ただ \(1\) 組存在する.
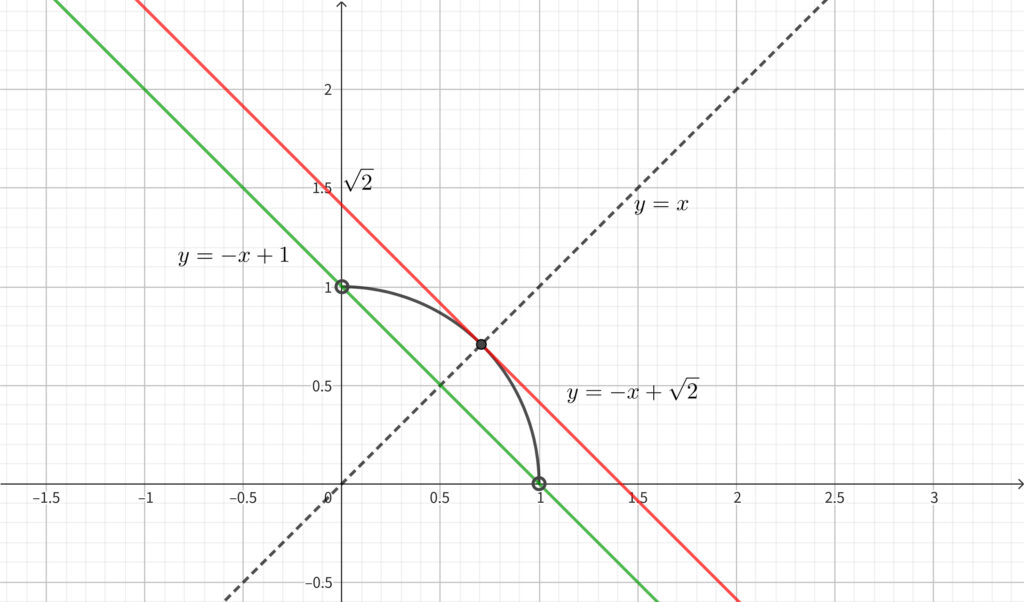
(1) の図より\(,\) \(y=x\) と \(y=-x+\sqrt{2}\) を同時に満たす正の実数 \(x,~y\) を求めると\(,\)
\begin{align}x=y=\frac{\sqrt{2}}{2}\end{align}
以上より\(,\)
\begin{align}a=\frac{\sqrt{2}}{2}~\left(x=y=\frac{\sqrt{2}}{2}\right)~~~~\cdots \fbox{答}\end{align}

quandle
(1) を解法②で解いている場合は\(,\) \(D=0\) のときを考えれば同様の解答になります.











コメント