創域理工学部(数理・先物・情計・生生・経シス)2024年第3問の問題文全文
関数 \(f(x)\) を
\begin{align}f(x)=\frac{\log{x}}{\sqrt{x}}~(x>0)\end{align}
と定める. ただし\(,\) \(\log{}\) は自然対数とする.
(1) 導関数 \(f^{\prime}(x)\) と第 \(2\) 次導関数 \(f^{\prime\prime}(x)\) をそれぞれ求めよ.
座標平面上の曲線 \(y=f(x)\) \((x>0)\) を \(C\) とおき\(,\) \(C\) の変曲点を \(\mathrm{P}\) とおく. \(C\) と \(x\) 軸の交点を \(\mathrm{Q}\) とする. \(C\) と直線 \(\mathrm{PQ}\) で囲まれた部分を \(A\) とし\(,\) \(A\) を \(x\) 軸の周りに \(1\) 回転して得られる回転体の体積を \(V\) とする.
(2) \(\mathrm{P}\) の座標を求めよ.
(3) \(V\) を求めよ.
(4) \(A\) の面積を求めよ.
(1) の解答
\(f^{\prime}(x)\) を求める
\begin{align}f^{\prime}(x)=\cfrac{\cfrac{1}{x}\cdot \sqrt{x}-\log{x}\cdot \cfrac{1}{2\sqrt{x}}}{x}\end{align}
\begin{align}=\frac{2-\log{x}}{2x\sqrt{x}}~~~~\cdots \fbox{答}\end{align}
\(f^{\prime\prime}(x)\) を求める
\begin{align}f^{\prime\prime}(x)=\cfrac{-\cfrac{1}{x}\cdot 2x\sqrt{x}-(2-\log{x})\cdot 3\sqrt{x}}{4x^3}\end{align}
\begin{align}=\frac{3\log{x}-8}{4x^2\sqrt{x}}~~~~\cdots \fbox{答}\end{align}
(2) の解答~\(f^{\prime\prime}(x)\) の符号を調べる~
\(4x^2\sqrt{x}>0\) より\(,\) \(f^{\prime\prime}(x)\) の符号は \(y=3\log{x}-8\) の符号と一致する.
\begin{align}\log{x}=\frac{8}{3}\Leftrightarrow x=e^{\frac{8}{3}}\end{align}
のとき\(,\) \(f^{\prime\prime}(x)=0\) となり\(,\) かつ\(,\) その前後で \(f^{\prime\prime}(x)\) は符号が変化する. よって\(,\) 変曲点 \(\mathrm{P}\) の座標は\(,\)
\begin{align}\mathrm{P}\left(e^{\frac{8}{3}},~\frac{8}{3e^{\frac{4}{3}}}\right)~~~~\cdots \fbox{答}\end{align}
(3) の解答
グラフの概形をかく
\begin{align}f^{\prime}(x)=0\end{align}
のとき\(,\)
\begin{align}\log{x}=2\Leftrightarrow x=e^2\end{align}
であるから\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|c|}\hline x & (0) & \cdots & e^2 & \cdots & \displaystyle e^{\frac{8}{3}} & \cdots \\ \hline f^{\prime}(x) & \times & + & 0 & – & – & – \\ \hline f^{\prime\prime}(x) & \times & – & – & – & 0 & + \\ \hline f(x) & \times & \nearrow \cap & \displaystyle \frac{2}{e} & \searrow \cap & \displaystyle \frac{8}{3e^{\frac{4}{3}}} & \searrow \cup \\ \hline \end{array}\end{align}
また\(,\)
\begin{align}\lim_{x\to +0}f(x)=-\infty ,~\lim_{x\to \infty}=0\end{align}
であるから\(,\) グラフの概形は以下のようになる.
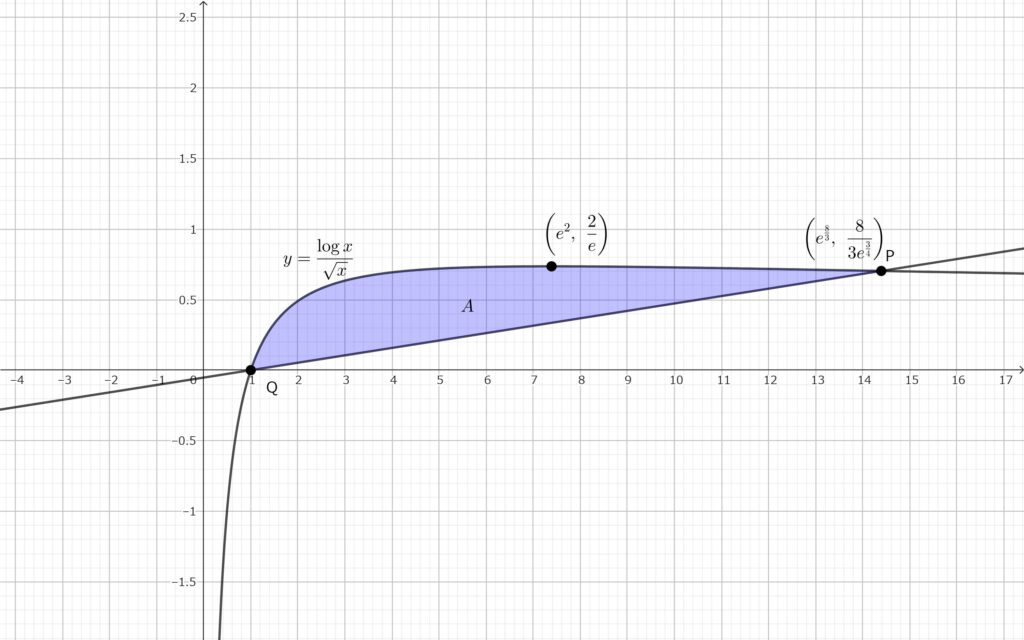
\(V\) を求める~円錐をくりぬく~
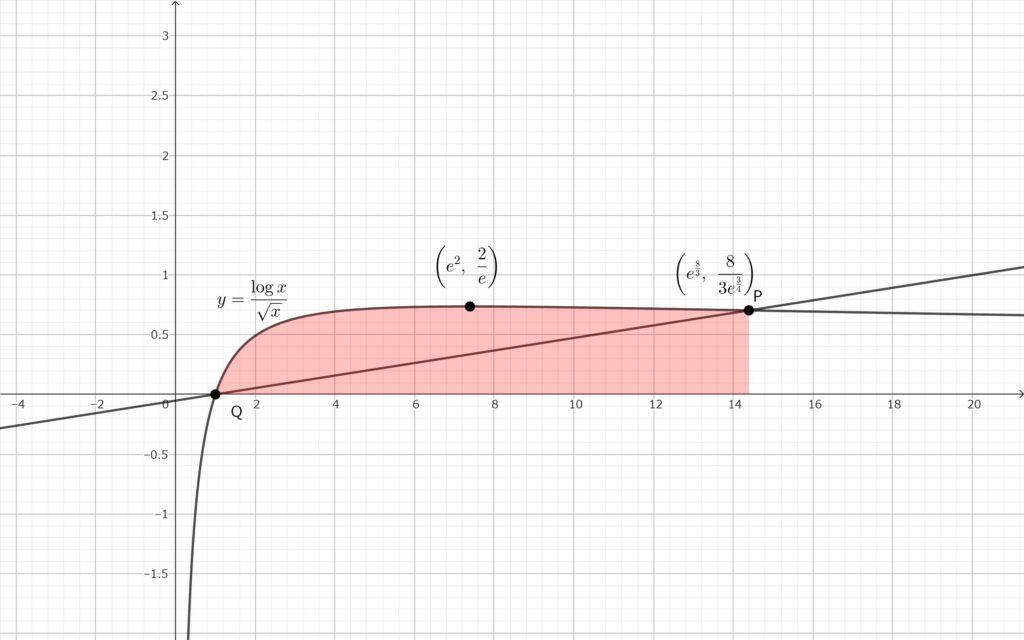
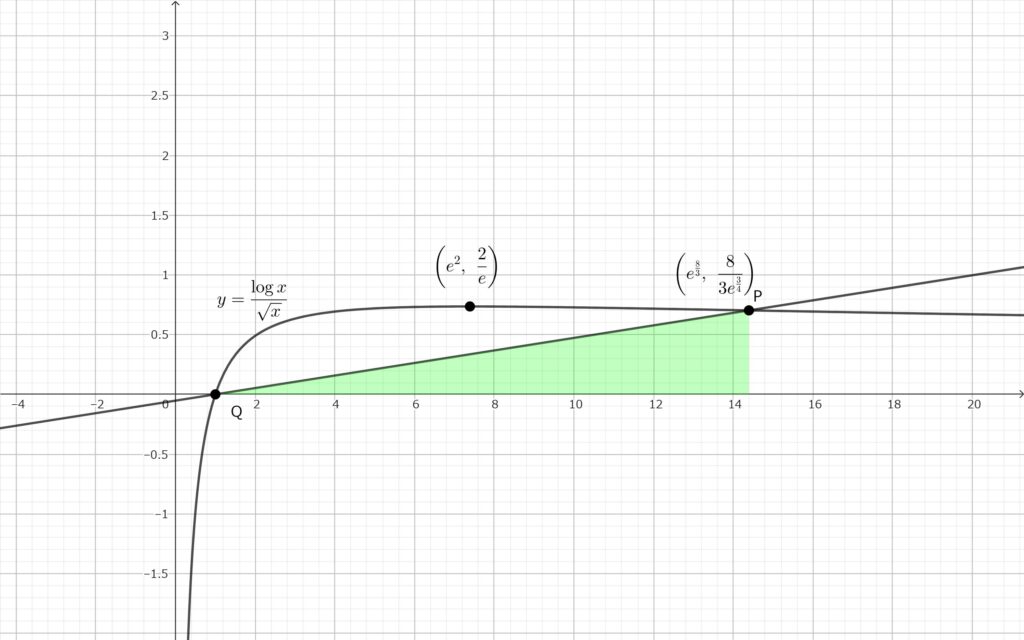
領域 \(A\) を \(x\) 軸に関して \(1\) 回転させたときにできる立体は\(,\) 下図の赤色部分を \(x\) 軸に関して \(1\) 回転させたときにできる立体から下図の緑色部分を \(x\) 軸に関して \(1\) 回転させたときにできる円錐をくりぬいてできる.
\begin{align}V=\pi \int_1^{e^{\frac{8}{3}}}\frac{(\log{x})^2}{x}dx-\frac{\pi}{3}\left(\frac{8}{3e^{\frac{4}{3}}}\right)^2\left(e^{\frac{8}{3}}-1\right)\end{align}
\begin{align}=\pi \biggl[\frac{1}{3}(\log{x})^3\biggr]_1^{e^{\frac{8}{3}}}-\frac{64}{27}\pi \left(1-e^{-\frac{8}{3}}\right)\end{align}
\begin{align}=\left(\frac{512}{81}-\frac{64}{27}+\frac{64}{27e^{\frac{8}{3}}}\right)\pi\end{align}
\begin{align}=\left(\frac{320}{81}+\frac{64}{27e^{\frac{8}{3}}}\right)\pi ~~~~\cdots \fbox{答}\end{align}

quandle
\begin{align}u(x)=x^2,~v(x)=\log{x}\end{align}
とおくと\(,\)
\begin{align}\frac{(\log{x})^2}{x}=u(v(x))v^{\prime}(x)\end{align}
ですので微分接触型になっています. \(u(x)\) を積分したものに \(v(x)\) を代入するだけで積分計算が完了します.
(4) の解答~直角三角形をくりぬく~
\(A\) の面積を \(S\) とおく. (3) の赤色部分の面積から緑色部分の面積を引けばよい.
\begin{align}S=\int_1^{e^{\frac{8}{3}}}\frac{\log{x}}{\sqrt{x}}dx-\frac{1}{2}\cdot \frac{8}{3e^{\frac{4}{3}}}\left(e^{\frac{8}{3}}-1\right)\end{align}
ここで\(,\) \(t=\sqrt{x}\) とおくと\(,\) \(t^2=x\) より\(,\)
\begin{align}2tdt=dx\end{align}
であり\(,\)
\begin{align}\begin{array}{|c|ccc|}\hline x & 1 & \to & \displaystyle e^{\frac{8}{3}}\\ \hline t & 1 & \to & \displaystyle e^{\frac{4}{3}}\\ \hline \end{array}\end{align}
であるから\(,\)
\begin{align}S=\int_1^{e^{\frac{4}{3}}}\frac{\log{t^2}}{t}\cdot 2tdt-\frac{4}{3}e^{\frac{4}{3}}+\frac{4}{3}e^{-\frac{4}{3}}\end{align}
\begin{align}=4\biggl[t\log{t}-t\biggr]_1^{e^{\frac{4}{3}}}-\frac{4}{3}e^{\frac{4}{3}}+\frac{4}{3}e^{-\frac{4}{3}}\end{align}
\begin{align}=4\left(\frac{4}{3}e^{\frac{4}{3}}-e^{\frac{4}{3}}+1\right)-\frac{4}{3}e^{\frac{4}{3}}+\frac{4}{3}e^{-\frac{4}{3}}\end{align}
\begin{align}=\frac{4}{3}e^{-\frac{4}{3}}+4~~~~\cdots \fbox{答}\end{align}






コメント