創域理工学部(建築・先化・電電・航空宇宙・社基工)2024年第2問の問題文全文
関数 \(f(x)\) を
\begin{align}f(x)=(x-3)^2-2|x-3|-3\end{align}
とする. \(a\) を正の実数\(,\) \(b\) を実数とする. 座標平面において\(,\) 曲線 \(y=f(x)\) を \(C,\) 直線 \(y=ax+b\) を \(\ell \) とおく.
(1) 関数 \(f(x)\) の極値を与える \(x\) の値をすべて求めよ. 極大値を与えるか極小値を与えるかも明記せよ.
(2) \(-4<b<-3\) のとき\(,\) 曲線 \(C\) と直線 \(\ell \) の共有点の個数が \(4\) 個となる正の実数 \(a\) の範囲を \(b\) を用いて表せ.
(3) \(0<a<2\) とする. 直線 \(\ell \) が点 \((3,~-3)\) を通るとき\(,\) 曲線 \(C\) と直線 \(\ell \) で囲まれた部分の面積を \(a\) を用いて表せ.
(1) の解答〜極値の定義を正しく理解できていますか?〜
\begin{align}f(x)=\left\{\begin{array}{cc}(x-3)^2-2(x-3)-3 & (x\geqq 3) \\ (x-3)^2+2(x-3)-3 & (x<3) \end{array}\right. \end{align}
\begin{align}=\left\{\begin{array}{cc}\{(x-3)-1\}^2-4 & (x\geqq 3) \\ \{(x-3)+1\}^2-4 & (x<3) \end{array}\right. \end{align}
\begin{align}=\left\{\begin{array}{cc}(x-4)^2-4 & (x\geqq 3) \\ (x-2)^2-4 & (x<3) \end{array}\right. \end{align}
グラフは以下のようになる.
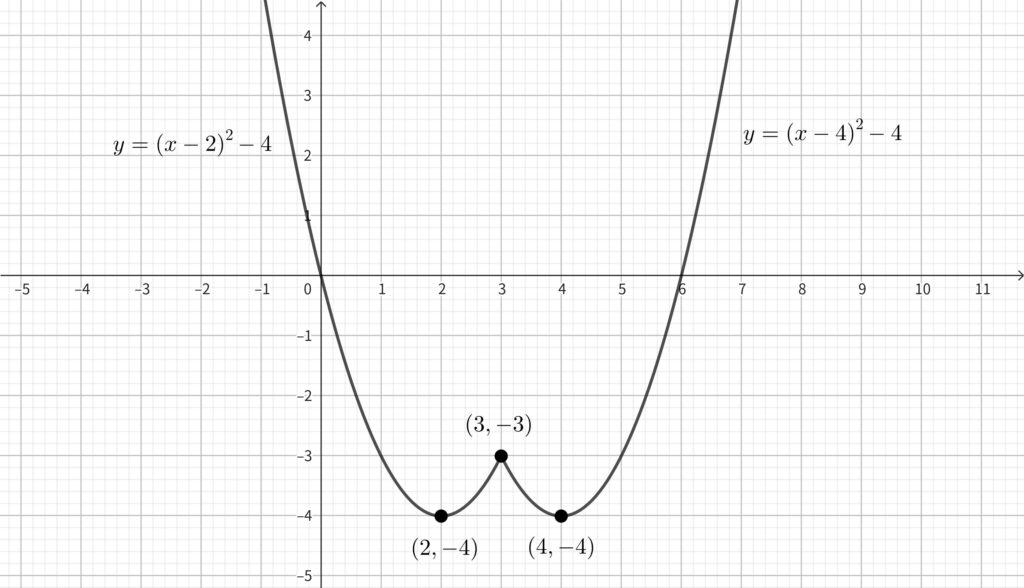
グラフより\(,\)
\begin{align}x=3~のとき極大値をとり,~x=2~\mathrm{or}~4~のとき極小値をとる~~~~\cdots \fbox{答}\end{align}

quandle
\(x=3\) のとき極大値を取るのですが違和感や自信がない人がいると思います.
「尖っているのに極大」と言っていいのか自信がないからだと思います.
極大値とは「局所的な最大値」のことです. 極大値の定義自体に微分可能性(もっと言えば連続性すらも)は一切含まれていませんので尖っていようが不連続だろうが局所的に最大値を取っていれば極大値になります. もっとちゃんと言うなら\(,\)
\(x=a\) で極大値をとるとは\(,\) ある正の実数 \(\varepsilon\) が存在して\(,\)
\begin{align}a-\varepsilon <x<a+\varepsilon~ならば~f(x)\leqq f(a)\end{align}
が成り立つことを意味しています.
(2) の解答〜3個になる場合を考える〜
\(-4<b<-3\) なる \(b\) に対して\(,\) \(y=ax+b\) の直線は \((0,~b)\)を通る.
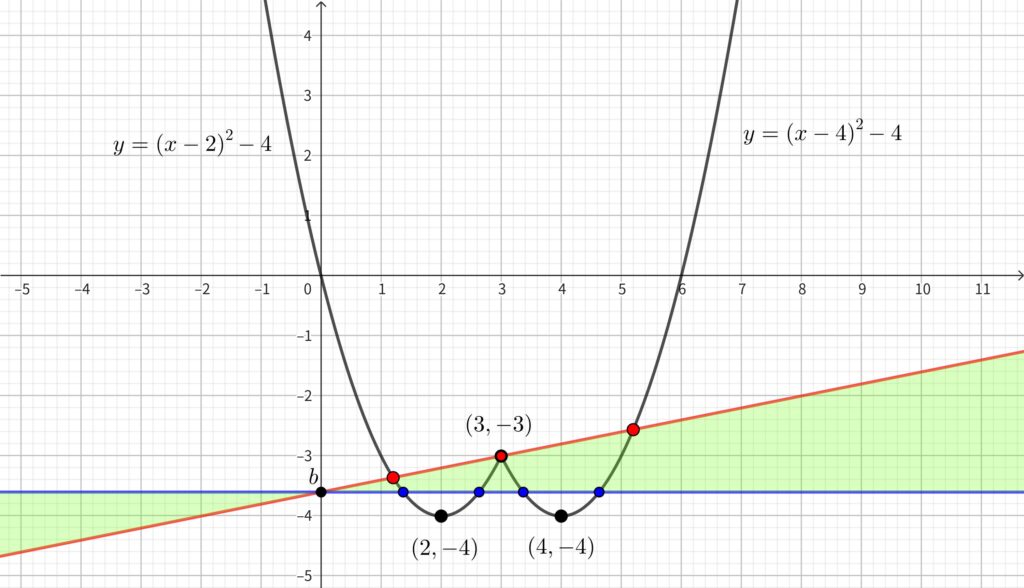
上図のように緑色部分を通る直線は共有点が \(4\) 個になる. 青色の直線は \(a=0\) のときを表し\(,\) 赤色の直線は \((3,~-3)\) を通る直線を表す.
\(y=ax+b\) が \((3,~-3)\) を通るとき\(,\)
\begin{align}-3=3a+b\end{align}
\begin{align}\therefore a=-\frac{1}{3}b-1\end{align}
であるから\(,\) 求める \(a\) の範囲は
\begin{align}0<a<-\frac{1}{3}b-1~~~~\cdots \fbox{答}\end{align}
(3) の解答〜\(\displaystyle \frac{1}{6}\) 公式の利用〜
\(\ell \) が点 \((3,-3)\) を通るので\(,\)
\begin{align}-3=3a+b\end{align}
\begin{align}\therefore b=-3a-3\end{align}
このとき\(,\)
\begin{align}\ell ~:~y=ax-3a-3\end{align}
\(C\) と \(\ell \) の交点の \(x\) 座標を求める.
\(x<3\) において\(,\)
\begin{align}(x-2)^2-4=ax-3a-3\end{align}
\begin{align}x^2-(a+4)x+3a+3=0\end{align}
\begin{align}(x-3)\{x-(a+1)\}=0\end{align}
\(x<3\) より\(,\)
\begin{align}x=a+1\end{align}
\(x\geqq 3\) において\(,\)
\begin{align}(x+2)^2-4=ax-3a-3\end{align}
\begin{align}x^2-(a-4)x+3a+3=0\end{align}
\begin{align}(x-3)\{x-(a+5)\}=0\end{align}
\begin{align}\therefore x=3,~a+5\end{align}
よって\(,\) 下図のようになる.
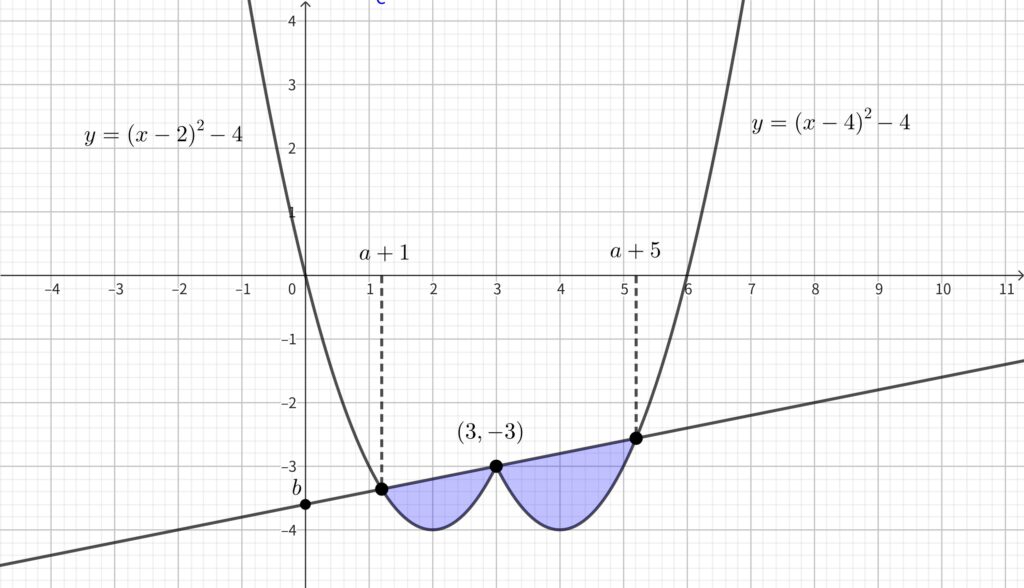
求める青色部分の面積を \(S\) とおく.
\begin{align}S=\int_{a+1}^3\{ax-3a-3-(x^2-4x)\}dx+\int_3^{a+5}\{ax-3a-3-(x^2-8x+12)\}dx\end{align}
\begin{align}=\int_{a+1}^3-(x-3)\{x-(a+1)\}dx+\int_3^{a+5}-(x-3)\{x-(a+5)\}dx\end{align}
\begin{align}=\frac{1}{6}\{3-(a+1)\}^3+\frac{1}{6}\{(a+5)-3\}^3\end{align}
\begin{align}=\frac{1}{6}\{(2-a)^3+(a+2)^3\}=\frac{6a^2+8}{3}~~~~\cdots \fbox{答}\end{align}

quandle
放物線と直線で囲まれる部分の面積は \(\displaystyle \frac{1}{6}\) 公式で瞬殺できますね!








コメント