問題文全文
\(t>1\) とする. 座標平面において, 連立不等式
\begin{align}0\leqq x\leqq e-1,~~1\leqq y\leqq t\log (x+1)\end{align}
の表す領域の面積を \(S_1(t)\) とし, 連立不等式
\begin{align}0\leqq x\leqq e-1,~~0\leqq y\leqq t\log (x+1),~~0\leqq y\leqq 1\end{align}
の表す領域の面積を \(S_2(t)\) とする. ただし, \(\log\) は自然対数, \(e\) は自然対数の底とする.
以下の問いに答えよ.
(1) 曲線 \(y=t\log (x+1)\) と直線 \(y=1\) の交点の \(x\) 座標を求めよ.
(2) \(S_1(t)\) を求めよ.
(3) \(S_2(t)\) を求めよ.
(4) \(\displaystyle \lim_{t\to \infty}\frac{S_1(t)-S_2(t)+t}{t-1}\) を求めよ.
(1)の解答
\begin{align}t\log (x+1)=1\Leftrightarrow x+1=e^{\frac{1}{t}}\end{align}
よって,
\begin{align}x=e^{\frac{1}{t}}-1.\end{align}
(2) の解答
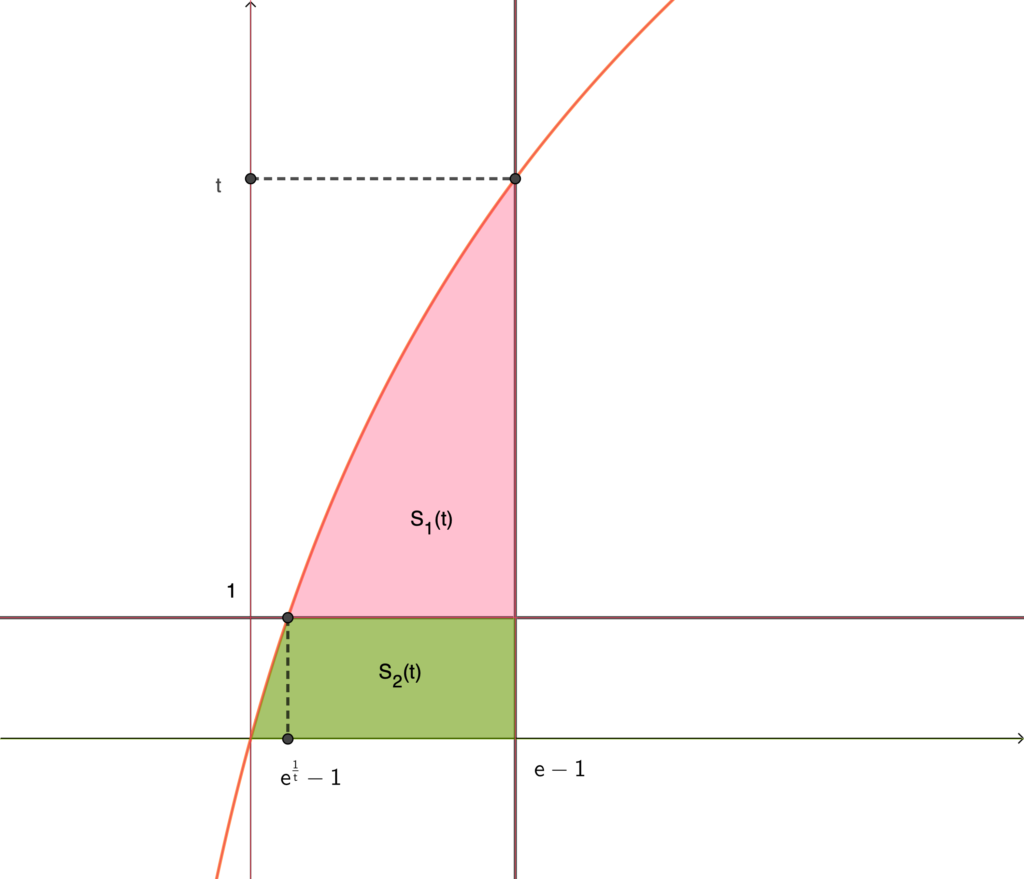
上図より
\begin{align}S_1(t)=\int_{e^{\frac{1}{t}}-1}^{e-1}\left\{t\log (x+1)-1\right\}dx\end{align}
\begin{align}=\biggl[t\left\{(x+1)\log (x+1)-x\right\}-x\biggr]_{e^{\frac{1}{t}}-1}^{e-1}\end{align}
\begin{align}=\biggl[t(x+1)\log (x+1)-(t+1)x\biggr]_{e^{\frac{1}{t}}-1}^{e-1}\end{align}
\begin{align}=te-(t+1)(e-1)-te^{\frac{1}{t}}\cdot \frac{1}{t}+(t+1)\left(e^{\frac{1}{t}}-1\right)=te^{\frac{1}{t}}-e.\end{align}
(3) の解答
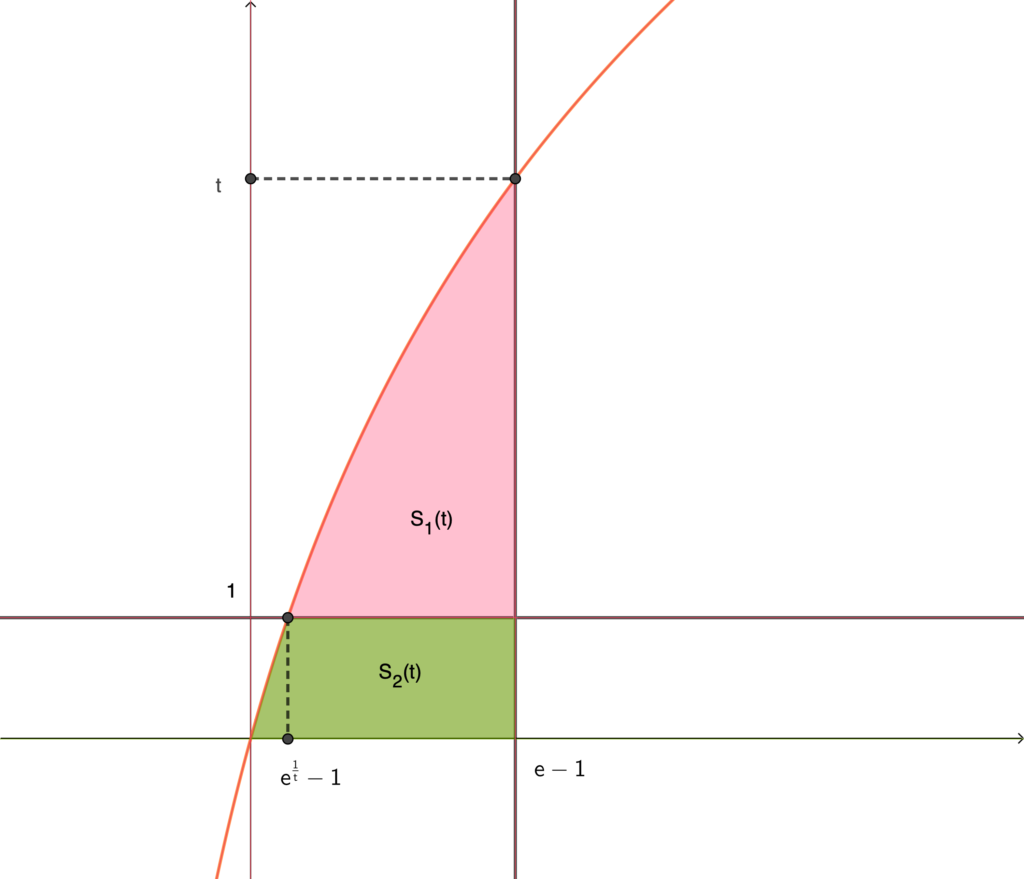
上図より
\begin{align}S_2(t)=\int_0^{e-1}t\log (x+1)dx-S_1(t)\end{align}
\begin{align}=\biggl[t\left\{(x+1)\log (x+1)-x\right\}\biggr]_0^{e-1}-\left(te^{\frac{1}{t}}-e\right)\end{align}
\begin{align}=te-(e-1)t-te^{\frac{1}{t}}+e=\left(1-e^{\frac{1}{t}}\right)t+e.\end{align}
(4) の解答
\begin{align}S_1(t)-S_2(t)+t\end{align}
\begin{align}=te^{\frac{1}{t}}-e-\left(t-te^{\frac{1}{t}}+e\right)+t=2te^{\frac{1}{t}}-2e\end{align}
であるから,
\begin{align}\lim_{t\to \infty}\frac{S_1(t)-S_2(t)+t}{t-1}=\lim_{t\to \infty}\frac{2te^{\frac{1}{t}}-2e}{t-1}\end{align}
\begin{align}=\lim_{n\to \infty}\cfrac{2e^{\frac{1}{t}}-\cfrac{2e}{t}}{1-\cfrac{1}{t}}=\frac{2\cdot 1-0}{1-0}=2.\end{align}




コメント