問題文全文
\(a\) は正の実数とする. 座標平面における曲線 \(C_1\) を,
\begin{align}C_1~:~y=ax^2+1\end{align}
とする. \(C_1\) 上の点 \((1,~a+1)\) における接線を \(l_1\) とし, 曲線 \(C_1\) の接線のうち \(l_1\) と直交するものを \(l_2\) とする. さらに, 直線 \(l_1\) と直線 \(l_2\) の交点の \(x\) 座標を \(t\) とする.
(1) 以下の問いに答えよ.
(a) 直線 \(l_1\), 直線 \(l_2\) の方程式を求めよ.
(b) 曲線 \(C_1\), 直線 \(l_1\) および直線 \(x=t\) によって囲まれる部分の面積を \(S_1\) とするとき, \(\displaystyle \frac{S_1}{a}\) を \(t\) を用いて表せ.
(c) \(a^2\) を \(t\) を用いて表せ. また, 曲線 \(C_1\), 直線 \(l_1\) および直線 \(l_2\) によって囲まれる部分の面積を \(S_2\) とするとき, \(\displaystyle \frac{S_2}{a}\) を \(t\) を用いて表せ.
(2) \(b\) を実数とし, 曲線 \(C_2\) を,
\begin{align}C_2~:~y=-a(x-2)^2+b\end{align}
とする.
(a) 曲線 \(C_1\) と曲線 \(C_2\) の共有点の個数を求めよ.
(b) 直線 \(l_1\) が曲線 \(C_2\) に接するとき, \(b\) を \(a\) を用いて表せ.
(c) 直線 \(l_1\) が曲線 \(C_2\) に接するとする. \(s>2\) とし, 点 \((s, -a(s-2)^2+b)\) における曲線 \(C_2\) の接線 \(l_3\) を考える. 曲線 \(C_2\), 直線 \(l_1\) および直線 \(l_3\) によって囲まれる部分の面積 \(S_3\) が, (1)(c) における \(S_2\) と等しくなるとき, \(s\) を \(a\) を用いて表せ.
2次関数と2接線の関係について
今回は入試頻出である「2次関数に引かれている2接線」が出てきます. 知っておくと格段に見通しが良くなる性質がいくつかありますのでまとめて紹介しておきます.

① 2 次関数 \(C~:~y=ax^2+\cdots\) と \(C\) の\(x=\alpha\) における接線 \(\ell_1\), \(x=\beta\) における接線 \(\ell_2\) で囲まれる部分の面積 \(S_1\) は
\begin{align}S_1=\frac{|a|}{12}(\beta -\alpha)^3\end{align}
で求められる.
② \(\ell_1\) と \(\ell_2\) の交点の \(x\) 座標は \(\displaystyle x=\frac{\alpha +\beta}{2}\) となる.
③ 上図において, 線分 \(\mathrm{AB}\) と \(C\) によって囲まれる面積を \(S_2\) とすると,
\begin{align}S_1~:~S_2=~1~:~2~\end{align}
である.
④ \(S_1\) の面積は \(\displaystyle x=\frac{\alpha +\beta}{2}\) を境目に面積が2等分される.
(1) の (a) の解答
\(y^{\prime}=2ax\) より
\begin{align}y=2a(x-1)+a+1\end{align}
\begin{align}\ell_1~:~y=2ax-a+1.\end{align}
\(\ell_1 \perp \ell_2\) より, \(\ell_2\) の傾きは \(\displaystyle -\frac{1}{2a}\) であるから,
\begin{align}\ell_2~:~y=-\frac{1}{2a}x+b\end{align}
とおく. \(C_1\) と \(\ell_2\) は接するので,
\begin{align}ax^2+1=-\frac{1}{2a}x+b\leftrightarrow ax^2+\frac{1}{2a}x-b+1=0~~\cdots 【1】\end{align}
の判別式 \(D_1\) とすると, \(D_1=0\) であるから,
\begin{align}D_1=\left(\frac{1}{2a}\right)^2-4\cdot a\cdot (-b+1)=0\end{align}
これを解いて,
\begin{align}b=1-\frac{1}{16a^3}\end{align}
よって,
\begin{align}\ell_2~:~y=-\frac{1}{2a}x+1-\frac{1}{16a^3}.\end{align}
(1) の (b) の解答
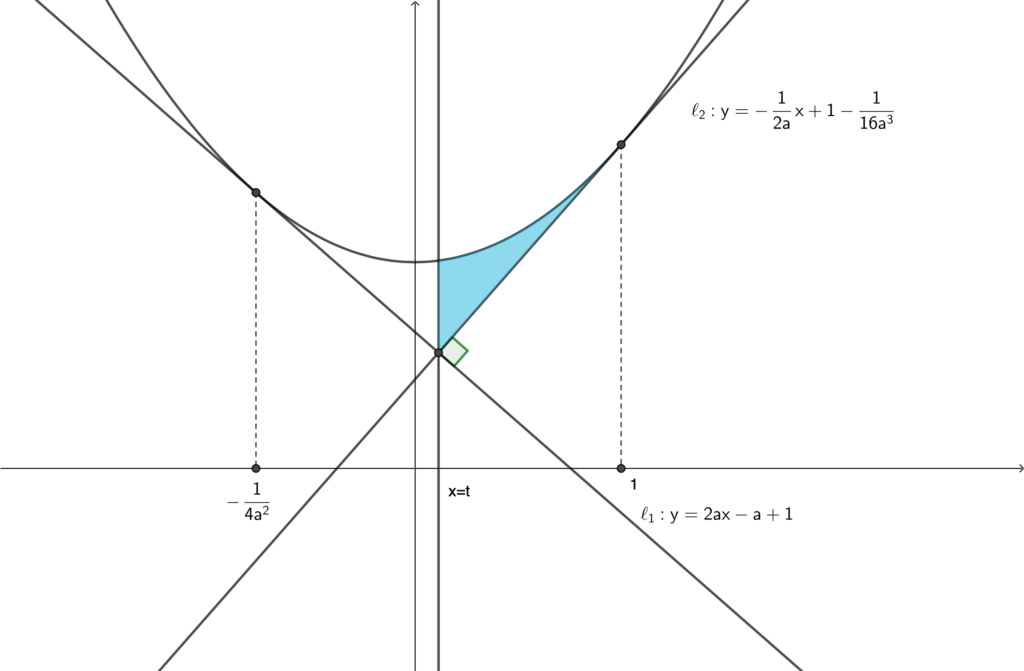
上図の青色領域の面積が \(S_1\) であるから,
\begin{align}S_1=\int_t^1\left\{ax^2+1-(2ax-a+1)\right\}dx\end{align}
\begin{align}=a\int_t^1(x-1)^2dx=a\biggl[\frac{1}{3}(x-1)^3\biggr]_t^1=\frac{a}{3}(1-t)^3\end{align}
よって,
\begin{align}\frac{S_1}{a}=\frac{1}{3}(1-t)^3.\end{align}

quandle
\(C_1\) と \(\ell_1\) は \(x=1\) で接しているのですから, 当然 \(x=1\) で重解を持つはずです. つまり \(C_1\) や \(\ell_1\) がどんなに複雑な式で書かれても引いた結果は \(a(x-1)^2\) になります. こういうところで余計な計算をしないようにしましょう.
(1) の (c) の着眼点
① 問題文から \(S_2\) は 2 次関数と 2 本の接線で囲まれた部分の面積ですから,
\begin{align}S_2=\frac{a}{12}(1-t)^3~~\cdots ✳︎\end{align}
であることはすぐに分かります. マーク式であれば瞬殺ですが, 今回は記述ですのできちんと答案を書かないといけません. 結果が ✴︎ になるということがわかっているので, 計算ミスに気付きやすくなります.
② 記述式ですから, \(S_2\) は \(\ell_1\) と \(\ell_2\) の交点を境に 2 つに分けて計算をする必要があります. その交点の \(x\) 座標は 2 つの接点の \(x\) 座標の平均になることを利用すれば簡単に結果がわかります. 実際は 2 つの直線の方程式を連立して求めることになりますが, 結果がわかっている分計算ミスに気付きやすくなります.
① も ② も「こうなるはず」と思って計算できる分, 精神的に楽になります.
③ \(S_2\) は \(x=t\) を境に 2 等分されます. つまり \(S_1\) 2 個分になるはずです. 容易に
\begin{align}S_2=2S_1=\frac{2a}{3}(1-t)^3\end{align}
であることが予想できます.
(1) の (c) の解答
\(C_1\) と \(\ell_2\) が接するので, 【1】は重解 \(\displaystyle x=-\frac{1}{4a^2}\) をもつ.

quandle
一般に \(ax^2+bx+c=0\) の重解は以下で求められます.
\begin{align}x=-\frac{b}{2a}\end{align}
\(\ell_1\) と \(\ell_2\) の交点の \(x\) 座標 \(t\) を求める.
\begin{align}2ax-a+1=-\frac{1}{2a}x+1-\frac{1}{16a^3}\Leftrightarrow \left(2a+\frac{1}{2a}\right)x=a-\frac{1}{16a^3}\end{align}
\begin{align}t=\cfrac{a-\cfrac{1}{16a^3}}{2a+\cfrac{1}{2a}}=\frac{16a^4-1}{32a^4+8a^2}\end{align}
\begin{align}=\frac{(4a^2-1)(4a^2+1)}{8a^2(4a^2+1)}=\frac{4a^2-1}{8a^2}\end{align}

quandle
接点の \(x\) 座標が \(\displaystyle x=-\frac{1}{4a^2}\) と \(x=1\) ですから, \(\ell_1\) と \(\ell_2\) の交点の \(x\) 座標は
\begin{align}t=\cfrac{-\cfrac{1}{4a^2}+1}{2}=\frac{4a^2-1}{8a^2}\end{align}
であることは最初に予想できますね.
よって,
\begin{align}8a^2t=4a^2-1\Leftrightarrow (4-8t)a^2=1\end{align}
\begin{align}a^2=\frac{1}{4(1-2t)}.\end{align}

quandle
\(\displaystyle t=\frac{1}{2}\) は
\begin{align}8a^2t=4a^2-1\end{align}
を満たさないので, \(\displaystyle t\neq \frac{1}{2}\) です.
\begin{align}S_2=\int_{-\frac{1}{4a^2}}^t\left\{ax^2+1-\left(-\frac{1}{2a}x+1-\frac{1}{16a^3}\right)\right\}dx+S_1\end{align}
\begin{align}=a\int_{-\frac{1}{4a^2}}^t\left(x+\frac{1}{4a^2}\right)^2dx+S_1=a\biggl[\frac{1}{3}\left(x+\frac{1}{4a^2}\right)^3\biggr]_{-\frac{1}{4a^2}}^t+S_1\end{align}

quandle
\(\displaystyle x=-\frac{1}{4a^2}\) で接していますね. (b) と同様に重解になるはずです.
\begin{align}=\frac{a}{3}\left(t+\frac{1}{4a^2}\right)^3+S_1=\frac{a}{3}(1-t)^3+\frac{a}{3}(1-t)^3=\frac{2a}{3}(1-t)^3\end{align}

quandle
\(\displaystyle a^2=\frac{1}{4(1-2t)}\) より, \(\displaystyle \frac{1}{4a^2}=1-2t\) とかけます. よって,
\begin{align}\frac{a}{3}\left(t+\frac{1}{4a^2}\right)^3=\frac{a}{3}(t+1-2t)^3=\frac{a}{3}(1-t)^3\end{align}
となります.
以上より,
\begin{align}\frac{S_2}{a}=\frac{2}{3}(1-t)^3.\end{align}
(2) の (a) の解答
\(C_1\) と \(C_2\) の共有点の個数は
\begin{align}ax^2+1=-a(x-2)^2+b\end{align}
の実数解の個数と一致する. 展開して整理すると,
\begin{align}2ax^2-4ax+4a-b+1=0~~\cdots 【2】\end{align}
となる. この 2 次方程式の判別式を \(D_2\) とおく.
\begin{align}\frac{D_2}{4}=(-2a)^2-2a(4a-b+1)=-2a(2a-b+1)\end{align}
\(-2a<0\) より,
\(2a-b+1>0\) のとき \(D_2<0\) より 0 個
\(2a-b+1=0\) のとき \(D_2=0\) より 1 個
\(2a-b+1<0\) のとき \(D_2>0\) より 2 個.
(2) の (b) の解答
\(\ell_1\) と \(C_2\) が接するので,
\begin{align}-a(x-2)^2+b=2ax-a+1\end{align}
つまり
\begin{align}ax^2-2ax+3a-b+1=0\end{align}
の判別式を \(D_3\) とおくと, \(D_3=0\) となる.
\begin{align}\frac{D_3}{4}=(-a)^2-a(3a-b+1)=0\end{align}
これを解いて,
\begin{align}b=2a+1.\end{align}
(2) の (c) の解答


quandle
\(S_3\) も 2 次関数と 2 接線に囲まれる部分の面積です. 接点の \(x\) 座標が \(x=1\) と \(x=s\) ですから, \(\ell_1\) と \(\ell_3\) の交点が
\begin{align} x=\frac{s+1}{2}\end{align}
であることと,
\begin{align}S_3=\frac{a}{12}(s-1)^3\end{align}
であることがすぐに予想できますね.
(b) より,
\begin{align}C_2~:~y=-a(x-2)^2+2a+1\end{align}
\(y^{\prime}=-2a(x-2)\) より, \(\ell_3\) の方程式は,
\begin{align}y=-2a(s-2)(x-s)-a(s-2)^2+2a+1\end{align}
\begin{align}\ell_3~:~y=-2a(s-2)x+as^2-2a+1\end{align}
\(\ell_1\) と \(\ell_3\) の交点を求める. \(a>0,~s>2\) より, \(a(s-1)\neq 0\) であることに注意して,
\begin{align}2ax-a+1=-2a(s-2)x+as^2-2a+1\end{align}
\begin{align}2(s-1)ax-as^2+a=0\end{align}
\begin{align}2(s-1)ax=a(s-1)(s+1)\end{align}
\begin{align}x=\frac{s+1}{2}\end{align}
\begin{align}S_3=\int_1^{\frac{s+1}{2}}[2ax-a+1-\{-a(x-2)^2+2a+1\}]dx+\int_{\frac{s+1}{2}}^s[-2a(s-2)x+as^2-2a+1-\{-a(x-2)^2+2a+1\}]dx\end{align}
\begin{align}=a\int_1^{\frac{s+1}{2}}(x-1)^2dx+a\int_{\frac{s+1}{2}}^s(x-s)^2dx=a\biggl[\frac{1}{3}(x-1)^3\biggr]_1^{\frac{s+1}{2}}+a\biggl[\frac{1}{3}(x-s)^3\biggr]_{\frac{s+1}{2}}^s\end{align}
\begin{align}=\frac{a}{3}\left(\frac{s+1}{2}-1\right)^3-\frac{a}{3}\left(\frac{s+1}{2}-s\right)^3=\frac{a}{24}(s-1)^3-\frac{a}{24}(1-s)^3=\frac{a}{12}(s-1)^3\end{align}
\(S_3=S_2\) より, \(\displaystyle \frac{S_3}{a}=\frac{S_2}{a}\) であるから,
\begin{align}\frac{1}{12}(s-1)^3=\frac{2}{3}(1-t)^3\Leftrightarrow (s-1)^3=8(1-t)^3\end{align}
\(s-1\) は実数であるから,
\begin{align}s-1=2(1-t)\end{align}
\begin{align}s=2-2t+1=3-2\cdot \frac{4a^2-1}{8a^2}=2+\frac{1}{4a^2}.\end{align}














コメント