問題文全文
関数 \(f(x)=-8x^3+6x+\sqrt{2}\) を考える.
(1) \(f(\cos{\theta})=0\) を満たす 3 つの \(\theta~(0\leqq \theta \leqq \pi)\) は
\begin{align}\frac{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emイウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi,~\frac{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emオカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi,~\frac{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\end{align}
である. 但し\(,\) \(\displaystyle 0\leqq \frac{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emイウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}<\frac{\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emオカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}<\frac{\fbox{$\hskip0.8emキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\leqq 1\) とする.
(2) 曲線 \(y=f(x)\) と \(x\) 軸で囲まれる 2 つの部分の面積の和は
\begin{align}\frac{\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-{\frac{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}\end{align}
である.
(1) の着眼点
いきなり \(\cos{\theta}\) を代入してもいいですが\(,\) たくさん \(\cos{\theta}\) を書くことになりそうなので\(,\) まずは \(x\) のまま因数分解できないかを確認します.
高次方程式の因数分解では因数定理を用います. 代入して 0 になる \(x\) の値を見つける必要があります.
注目すべきは \(x^3\) の係数である -8 と\(,\) 定数項である \(\sqrt{2}\) です. 特に定数項の \(\sqrt{2}\) の縛りが強く\(,\) \(x=k\sqrt{2}\) という形であることが予想されます.
また \(x^3\) の係数が -8 と大きいのでこれを消すように \(k\) の値を考えます.
すると \(\displaystyle f\left(-\frac{\sqrt{2}}{2}\right)=0\) であることが発見できます.
(1) の解答
\begin{align}f\left(-\frac{\sqrt{2}}{2}\right)=0\end{align}
より\(,\)
\begin{align}f(x)=-8\left(x+\frac{\sqrt{2}}{2}\right)\left(x^2-\frac{\sqrt{2}}{2}x-\frac{1}{4}\right)\end{align}
\(f(x)=0\) のとき\(,\)
\begin{align}x+\frac{\sqrt{2}}{2}=0~or~x^2-\frac{\sqrt{2}}{2}x-\frac{1}{4}=0\end{align}
\begin{align}x=-\frac{\sqrt{2}}{2}~or~x=\cfrac{\cfrac{\sqrt{2}}{2}\pm \sqrt{\cfrac{1}{2}+1}}{2}=\frac{\sqrt{2}\pm\sqrt{6}}{4}\end{align}
\(f(\cos{\theta})=0\) のとき
\begin{align}\cos{\theta}=\frac{\sqrt{2}+\sqrt{6}}{4},~\frac{\sqrt{2}-\sqrt{6}}{4},~-\frac{\sqrt{2}}{2}\end{align}
\(0\leqq \theta \leqq \pi\) より\(,\)
\begin{align}\theta =\frac{\pi}{12},~\frac{7}{12}\pi,~\frac{3}{4}\pi.\end{align}

quandle
\begin{align}\sin{\frac{\pi}{12}}=\frac{\sqrt{6}-\sqrt{2}}{4},~\cos{\frac{\pi}{12}}=\frac{\sqrt{6}+\sqrt{2}}{4}\end{align}
の 2 つは意外と入試で出る値なので知っておくといいです. この 2 つさえ覚えておけば
\begin{align}\frac{5}{12}\pi,~\frac{7}{12}\pi,~\frac{11}{12}\pi\end{align}
などの三角関数をすぐに求めることができます.
(2) の着眼点
(1) から \(f(x)=0\) の解がわかっています. それぞれを
\begin{align}\alpha =-\frac{\sqrt{2}}{2},~\beta =\frac{\sqrt{2}-\sqrt{6}}{4},~\gamma =\frac{\sqrt{2}+\sqrt{6}}{4}\end{align}
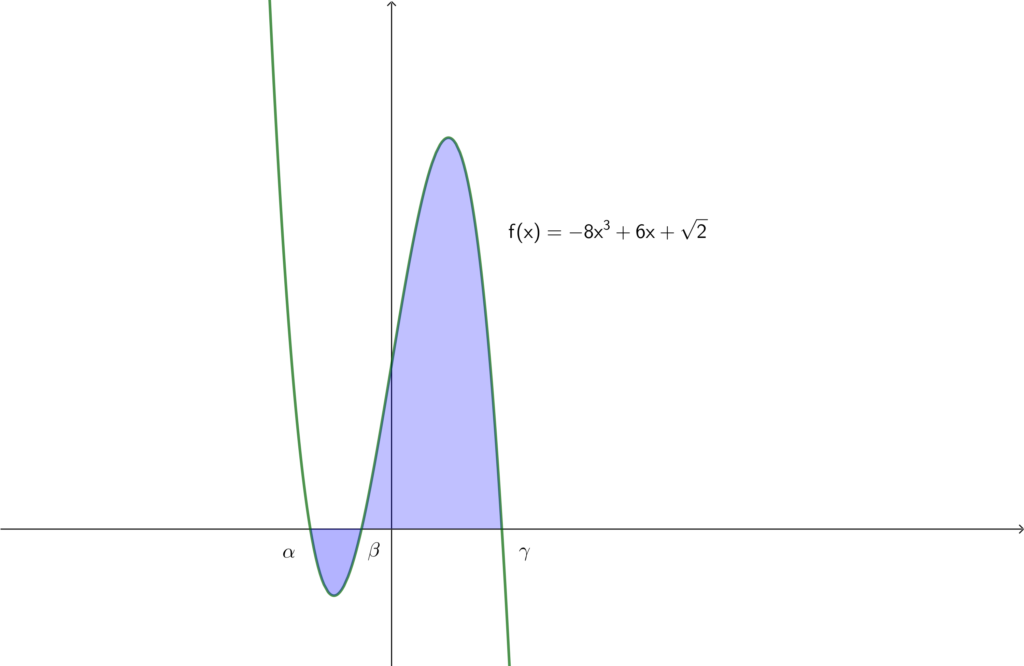
とすると\(,\) \(y=f(x)\) と \(x\) 軸との交点の \(x\) 座標は \(x=\alpha,~\beta,~\gamma\) です.
求める面積は
\begin{align}S=-\int_{\alpha}^{\beta}f(x)dx+\int_{\beta}^{\gamma}f(x)dx\end{align}
と表されます. この計算をいかに効率よくやるかでかかってくる時間が変わってきます.
一旦 \(f(x)\) の原始関数の 1 つを \(F(x)\) として
\begin{align}S=F(\alpha)-2F(\beta)+F(\gamma)\end{align}
と書きます. あとはそれぞれを計算すると比較的楽に計算できます. 先に
\begin{align}{\alpha}^2,~{\alpha}^4,~{\beta}^2,~{\beta}^4,~{\gamma}^2,~{\gamma}^4\end{align}
を計算しておくとよいです.
(2) の解答
\begin{align}\alpha =-\frac{\sqrt{2}}{2},~\beta =\frac{\sqrt{2}-\sqrt{6}}{4},~\gamma =\frac{\sqrt{2}+\sqrt{6}}{4}\end{align}
とおく. 上図より\(,\) 求める面積 \(S\) は
\begin{align}S=-\int_{\alpha}^{\beta}f(x)dx+\int_{\beta}^{\gamma}f(x)dx\end{align}
とかける. \(f(x)\) の原始関数の 1 つを \(F(x)\) とすると\(,\)
\begin{align}F(x)=\int f(x) dx=-2x^4+3x^2+\sqrt{2}x+C\end{align}
であり\(,\)
\begin{align}S=\biggl[F(x)\biggr]_{\alpha}^{\beta}+\biggl[F(x)\biggr]_{\beta}^{\gamma}\end{align}
\begin{align}=-(F(\beta)-F(\alpha))+F(\gamma)-F(\beta)=F(\alpha)-2F(\beta)+F(\gamma)\end{align}
と表される. ここで\(,\)
\begin{align}{\alpha}^2=\frac{1}{2},~{\alpha}^4=\frac{1}{4},~{\beta}^2=\frac{2-\sqrt{3}}{4},~{\beta}^4=\frac{7-4\sqrt{3}}{16},~{\gamma}^2=\frac{2+\sqrt{3}}{4},~{\gamma}^4=\frac{7+4\sqrt{3}}{16}\end{align}
であるから\(,\)
\begin{align}F(\alpha)=-2\cdot \frac{1}{4}+3\cdot \frac{1}{2}+\sqrt{2}\cdot \left(-\frac{\sqrt{2}}{2}\right)=0\end{align}
\begin{align}F(\beta)=-2\cdot \frac{7-4\sqrt{3}}{16}+3\cdot \frac{2-\sqrt{3}}{4}+\sqrt{2}\cdot \frac{\sqrt{2}-\sqrt{6}}{4}=\frac{9-6\sqrt{3}}{8}\end{align}
\begin{align}F(\gamma)=-2\cdot \frac{7+4\sqrt{3}}{16}+3\cdot \frac{2+\sqrt{3}}{4}+\sqrt{2}\cdot \frac{\sqrt{2}+\sqrt{6}}{4}=\frac{9+6\sqrt{3}}{8}\end{align}
となる. よって\(,\)
\begin{align}S=0-2\cdot \frac{9-6\sqrt{3}}{8}+\frac{9+6\sqrt{3}}{8}\end{align}
\begin{align}=\frac{9\sqrt{3}}{4}-\frac{9}{8}.\end{align}






コメント