C方式・グローバル方式2022年第３問の問題文全文
関数 \(f(x)=\cos{x}+\sin{x}\cos{x}~(0\leqq x \leqq 2\pi )\) について考える. 以下の問いに答えよ.
(1) \(f(x)=0\) を満たす \(x\) の値を小さい順に \(a_1,~a_2\) とすると\(,\)
\begin{align}a_1=\frac{\fbox{$\hskip0.8emテ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emト\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi ,~a_2=\frac{\fbox{$\hskip0.8emナ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emニ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi \end{align}
である.
(2) \(f^{\prime}(x)=0\) を満たす \(x\) の値を小さい順に \(b_1,~b_2,~b_3\) とすると\(,\)
\begin{align}b_1=\frac{\fbox{$\hskip0.8emヌ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emネ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi ,~b_2=\frac{\fbox{$\hskip0.8emノ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emハ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi ,~b_3=\frac{\fbox{$\hskip0.8emヒ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emフ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi \end{align}
である. ただし \(f^{\prime}(x)\) は \(f(x)\) の導関数である.
(3) \(x\) が \(0 \leqq x \leqq 2\pi \) の範囲を動くとき\(,\) \(f(x)\) は \(\displaystyle x=\frac{\fbox{$\hskip0.8emヘ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emホ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi \) で最大値 \(\displaystyle \frac{\fbox{$\hskip0.8emマ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emミ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emム\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) をとる.
(4)
\begin{align}\int_0^{2\pi}|f(x)|dx=\fbox{$\hskip0.8emメ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
である.
(1) の解答〜\(\cos{x}\) でくくる〜
\begin{align}\cos{x}(1+\sin{x})=0\end{align}
\begin{align}\cos{x}=0~~\mathrm{or}~~\sin{x}=-1\end{align}
\begin{align}a_1=\frac{1}{2}\pi ,~a_2=\frac{3}{2}\pi~~~~\cdots \fbox{答}\end{align}
テ：１ ト：２ ナ：３ ニ：２
(2) の解答〜\(\sin{x}\) で揃える〜
\begin{align}f^{\prime}(x)=-\sin{x}(1+\sin{x})+\cos^2{x}=-2\sin^2{x}-\sin{x}+1\end{align}
\(f^{\prime}(x)=0\) のとき\(,\)
\begin{align}2\sin^2{x}+\sin{x}-1=0\end{align}
\begin{align}(\sin{x}+1)(2\sin{x}-1)=0\end{align}
\begin{align}\sin{x}=-1~~\mathrm{or}~~\frac{1}{2}\end{align}
\begin{align}b_1=\frac{1}{6}\pi ,~b_2=\frac{5}{6}\pi ,~b_3=\frac{3}{2}\pi~~~~\cdots \fbox{答}\end{align}
ヌ：１ ネ：６ ノ：５ ハ：６ ヒ：３ フ：２
(3) の解答〜増減表をかく〜
\begin{align}\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle \frac{\pi}{6} & \cdots & \displaystyle \frac{5}{6}\pi & \cdots & \displaystyle \frac{3}{2}\pi & \cdots & 2\pi \\ \hline f^{\prime}(x) & {} & + & 0 & – & 0 & + & 0 & + & {} \\ \hline f(x) & 1 & \nearrow & \displaystyle \frac{3\sqrt{3}}{4} & \searrow & \displaystyle -\frac{3\sqrt{3}}{4} & \nearrow & 0 & \nearrow & 1 \\ \hline \end{array}\end{align}
増減表より\(,\)
\(\displaystyle x=\frac{1}{6}\pi\) のとき\(,\) 最大値 \(\displaystyle \frac{3}{4}\sqrt{3}\) をとる. \(\cdots \fbox{答}\)
へ：１ ホ：６ マ：３ ミ：４ ム：３
(4) の着眼点〜絶対値の外し方〜
絶対値がついているので\(,\) \(f(x)\) が正になる範囲と負になる範囲を調べる必要があります.
(3) の増減表から
\begin{align}f\left(\frac{\pi}{6}\right)=\frac{3\sqrt{3}}{4}>0,~f\left(\frac{5}{6}\pi \right)=-\frac{3\sqrt{3}}{4}<0\end{align}
であり\(,\) \(f(x)\) は連続ですから\(,\) \(\displaystyle \frac{\pi}{6} \leqq x \leqq \frac{5}{6}\pi \) の範囲に \(f(x)\) が正から負に切り替わる瞬間があるはずです.
そしてそれはすでに (1) で求めていて\(,\) \(\displaystyle x=\frac{\pi}{2}\) のときです.
これまでの問題の流れをきちんと理解していれば (4) は特に何も調べなくても絶対値を外すことができます. 参考までにグラフは以下のようになります.
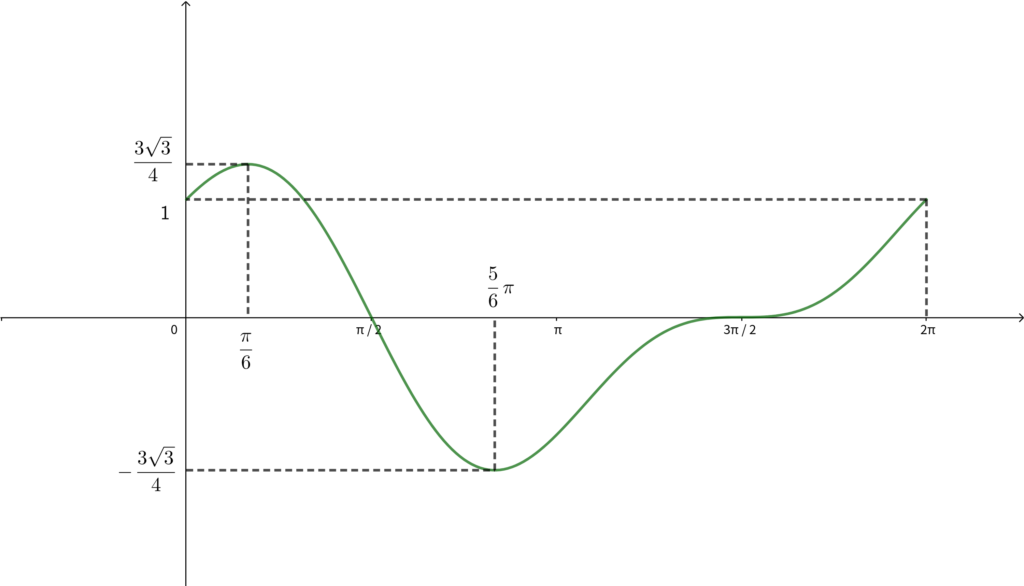\(f(x)=\cos{x}+\sin{x}\cos{x}\) のグラフ
(4) の解答〜周期性に注目して計算をさぼる〜
\(f(x)\) の原始関数の \(1\) つを \(F(x)\) とおくと\(,\) \(\displaystyle f(x)=\cos{x}+\frac{1}{2}\sin{2x}\) より\(,\)
\begin{align}F(x)=\sin{x}-\frac{1}{4}\cos{2x}\end{align}
\begin{align}\int_0^{2\pi}|f(x)|dx\end{align}
\begin{align}=\int_0^{\frac{\pi}{2}}f(x)dx-\int_{\frac{\pi}{2}}^{\frac{3}{2}\pi}f(x)dx+\int_{\frac{3}{2}\pi}^{2\pi}f(x)dx\end{align}
\begin{align}=\biggl[F(x)\biggr]_0^{\frac{\pi}{2}}-\biggl[F(x)\biggr]_{\frac{\pi}{2}}^{\frac{3}{2}\pi}+\biggl[F(x)\biggr]_{\frac{3}{2}\pi}^{2\pi}\end{align}
\begin{align}=2F\left(\frac{\pi}{2}\right)-2F\left(\frac{3}{2}\pi \right)-F(0)+F(2\pi)\end{align}
\begin{align}=2\left(1+\frac{1}{4}\right)-2\left(-1+\frac{1}{4}\right)=4~~~~\cdots \fbox{答}\end{align}
quandle
\(F(x)\) は周期 \(2\pi \) の関数です. なぜなら \(\sin{x}\) の周期が \(2\pi \) で \(\cos{2x}\) の周期が \(\pi \) ですからその最小公倍数の \(2\pi \) が周期となるからです. 周期が \(2\pi \) ということがわかっていれば \(-F(0)+F(2\pi )=0\) であることが直ちにわかるので計算不要です！
メ：４
コメント