東京理科大学先進工学部2022年第４問

先進工学

2022.03.12

先進工学部2022年第４問の問題文全文
(1) の解答
(2) の解答〜積の微分・合成関数の微分〜
(3) の解答〜増減表をかいて調べる〜
(4) の解答〜微分接触系の積分〜
1. 微分接触系の積分
2. 解答

先進工学部2022年第４問の問題文全文

関数 $f(x)$ を$,$

\begin{align}f(x)=xe^{-4x^2+1}\end{align}

と定める. ここで$,$ $e$ は $\displaystyle e=\lim_{k\to 0}(1+k)^{\frac{1}{k}}$ によって定まる実数である.

(1) $f(1)=\fbox{$\hskip0.8em（あ）\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ である.

(2) $f(x)$ を微分すると$,$

\begin{align}f^{\prime}(x)=\fbox{$\hskip0.8em（い）\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}

となる.

(3) $x$ が $0\leqq x \leqq 1$ の範囲を動くとき$,$ $f(x)$ は$,$ $x=~\fbox{$\hskip0.8em（う）\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ のとき最大値 $\fbox{$\hskip0.8em（え）\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ をとり$,$ $x=~\fbox{$\hskip0.8em（お）\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ のとき最小値 $\fbox{$\hskip0.8em（か）\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ をとる.

(4) 座標平面上で$,$ 原点 $\mathrm{O}$ と点 $(1,~f(1))$ の $2$ 点を通る直線を $\ell $ とおき$,$ 直線 $\ell $ と曲線 $y=f(x)~(x>0)$ で囲まれた図形を $D$ とおく. このとき $D$ の面積は $\fbox{$\hskip0.8em（き）\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ である.

(1) の解答

\begin{align}f(1)=1\cdot e^{-4\cdot 1+1}=e^{-3}~~~~\cdots \fbox{答}\end{align}

（あ） $\displaystyle e^{-3}$

(2) の解答〜積の微分・合成関数の微分〜

\begin{align}f^{\prime}(x)=e^{-4x^2+1}+x(-8xe^{-4x^2+1})\end{align}

\begin{align}=(1-8x^2)e^{-4x^2+1}~~~~\cdots \fbox{答}\end{align}

（い） $\displaystyle (1-8x^2)e^{-4x^2+1}$

(3) の解答〜増減表をかいて調べる〜

$\displaystyle e^{-4x^2+1}>0$ であるから$,$ $f^{\prime}(x)$ の符号と $1-8x^2$ の符号は一致する. よって増減表は以下のようになる.

\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline x & 0 & \cdots & \displaystyle \frac{\sqrt{2}}{4} & \cdots & 1 \\ \hline f^{\prime}(x) & {} & + & 0 & – & {} \\ \hline f(x) & 0 & \nearrow & \displaystyle \frac{\sqrt{2e}}{4} & \searrow & e^{-3} \\ \hline \end{array}\end{align}

増減表より$,$

$\displaystyle x=\frac{\sqrt{2}}{4}$ のとき最大値 $\displaystyle \frac{\sqrt{2e}}{4}~~~~\cdots \fbox{答}$

$x=0$ のとき最小値 $0~~~~\cdots \fbox{答}$

（う） $\displaystyle \frac{\sqrt{2}}{4}$ （え） $\displaystyle \frac{\sqrt{2e}}{4}$ （お）$0$ （か） $0$

(4) の解答〜微分接触系の積分〜

微分接触系の積分

関数 $f(x)$ の原始関数の $1$ つを $F(x)$ とするとき$,$

\begin{align}\int f(g(x))g^{\prime}(x)dx=F(g(x))+C\end{align}

と計算できます. これを「微分接触系の積分」と当サイトでは呼んでいます.

詳細は以下の記事にまとめていますのでご参照ください. 微分接触系と判断できたら置換積分せずに一気に積分計算できます. 必須の計算テクニックですのでできるようにしておきましょう.

（後日アップ予定）

今回の問題では $\displaystyle \int xe^{-4x^2+1}dx$ が微分接触系になっています.

解答

(1) より $\ell $ は原点と $(1,~e^{-3})$ を通る直線なので

\begin{align}\ell ~:~y=e^{-3}x\end{align}

また$,$ $D$ は以下の図のようになる.

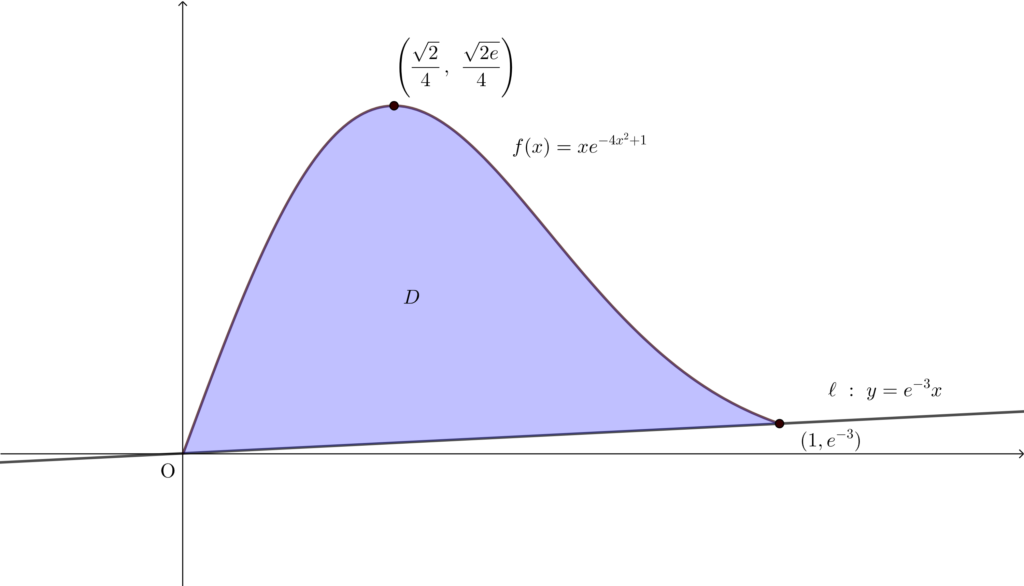
求める面積は

\begin{align}\int_0^1\left(xe^{-4x^2+1}-e^{-3}x\right)dx\end{align}

\begin{align}=\int_0^1\left\{-\frac{1}{8}(-8x)e^{-4x^2+1}-e^{-3}x\right\}dx\end{align}

\begin{align}=\biggl[-\frac{1}{8}e^{-4x^2+1}-\frac{1}{2}e^{-3}x\biggr]_0^1\end{align}

\begin{align}=-\frac{1}{8}e^{-3}-\frac{1}{2}e^{-3}+\frac{1}{8}e=\frac{1}{8}e-\frac{5}{8}e^{-3}~~~~\cdots \fbox{答}\end{align}