先進工学部2023年第4問の問題文全文
以下の問いに答えなさい.
関数 \(f(x)\) を
\begin{align}f(x)=\log{(x^2+e)}\end{align}
と定め\(,\) 座標平面上の曲線 \(y=f(x)\) を考える. ただし\(,\) \(\log \) は自然対数である. ここで\(,\) \(e\) は \(\displaystyle e=\lim_{t\to 0}(1+t)^{\frac{1}{t}}\) によって定まる実数とする.
(1) 関数 \(f(x)\) の導関数は \(f^{\prime}(x)=~\fbox{$\hskip0.4em(あ)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}~\) である.
(2) 点 \((\sqrt{e},~f(\sqrt{e}))\) における曲線 \(y=f(x)\) の接線 \(\ell \) の方程式は\(,\)
\begin{align}\fbox{$\hskip0.4em(い)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\end{align}
となる.
(3) 定積分 \(\displaystyle \int_0^{\sqrt{e}}\frac{e}{x^2+e}dx\) の値は\(,\)
\begin{align}\fbox{$\hskip0.4em(う)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\end{align}
である.
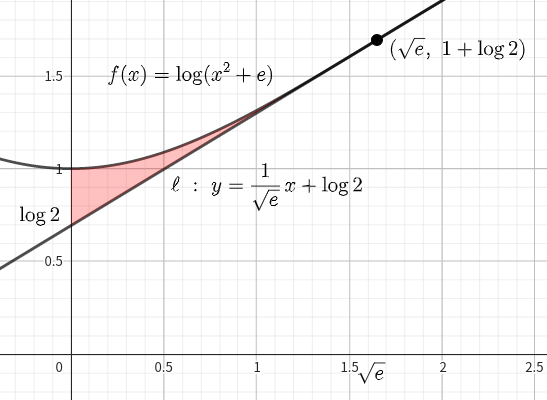
(4) 曲線 \(y=f(x)\) と (2) で求めた接線 \(\ell \) と \(y\) 軸で囲まれた図形を \(D\) とする. このとき\(,\) \(D\) の面積は \(\fbox{$\hskip0.4em(え)\hskip0.4em\Rule{0pt}{0.4em}{0.4em}$}\) である.
(1) の解答〜合成関数の微分〜
\begin{align}f^{\prime}(x)=\frac{2x}{x^2+e}~~~~\cdots \fbox{答}\end{align}
(あ)\(\displaystyle \frac{2x}{x^2+e}\)
(2) の解答〜接線の公式〜
\begin{align}f^{\prime}(\sqrt{e})=\frac{2\sqrt{e}}{e+e}=\frac{1}{\sqrt{e}}\end{align}
\begin{align}f(\sqrt{e})=\log{(e+e)}=1+\log{2}\end{align}
より\(,\) 接線 \(\ell \) の方程式は\(,\)
\begin{align}y=\frac{1}{\sqrt{e}}(x-\sqrt{e})+1+\log{2}\end{align}
\begin{align}\therefore \ell ~:~y=\frac{1}{\sqrt{e}}x+\log{2}~~~~\cdots \fbox{答}\end{align}
(い)\(\displaystyle y=\frac{1}{\sqrt{e}}x+\log{2}\)
(3) の解答〜\(\displaystyle \int \frac{dx}{x^2+a^2}\) 型は \(a\tan{\theta} \) で置換〜
\(x=\sqrt{e}\tan{\theta}\) とおくと\(,\) \(\displaystyle dx=\frac{\sqrt{e}}{\cos^2{\theta}}d\theta \) であり\(,\)
\begin{align}\begin{array}{|c|ccc|}\hline x & 0 & \to & \sqrt{e}\\ \hline \theta & 0 & \to & \displaystyle \frac{\pi}{4}\\ \hline \end{array}\end{align}
であるから\(,\)
\begin{align}\int_0^{\sqrt{e}}\frac{e}{x^2+e}dx=\int_0^{\frac{\pi}{4}}\frac{e}{e\tan^2{\theta}+e}\cdot \frac{\sqrt{e}}{\cos^2{\theta}}d\theta \end{align}
\begin{align}=\biggl[\sqrt{e}\theta \biggr]_0^{\frac{\pi}{4}}=\frac{\sqrt{e}}{4}\pi ~~~~\cdots \fbox{答}\end{align}
(う)\(\displaystyle \frac{\sqrt{e}}{4}\pi\)
(4) の解答〜台形をくり抜く〜
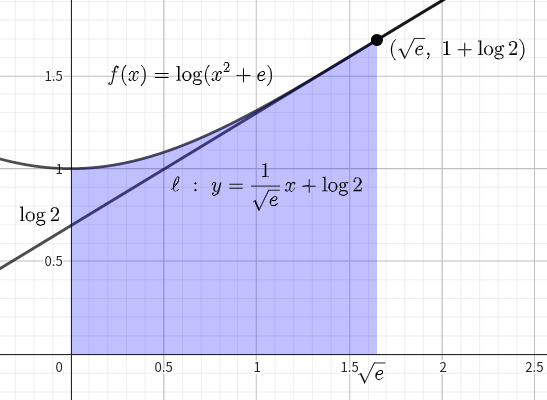
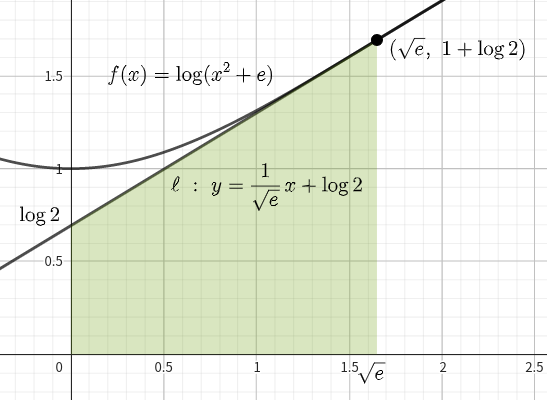
\(D\) (赤色部分)は青色部分から台形(緑色部分)をくり抜いたものであるから\(,\) \(D\) の面積 \(S\) は
\begin{align}S=\int_0^{\sqrt{e}}\log{(x^2+e)}dx-\frac{1}{2}(\log{2}+1+\log{2})\sqrt{e}\end{align}
\begin{align}=\biggl[x\log{(x^2+e)}\biggr]_0^{\sqrt{e}}-\int_0^{\sqrt{e}}x\cdot \frac{2x}{x^2+e}dx-\frac{\sqrt{e}}{2}(1+2\log{2})\end{align}

quandle
\begin{align}\log{(x^2+e)}=1\cdot \log{(x^2+e)}=(x)^{\prime}\cdot \log{(x^2+e)}\end{align}
と見て部分積分を利用しましょう!
\begin{align}=\sqrt{e}\log{2e}-2\int_0^{\sqrt{e}}\left(1-\frac{e}{x^2+e}\right)dx-\frac{\sqrt{e}}{2}(1+2\log{2})\end{align}

quandle
\begin{align}\int \frac{2x^2}{x^2+e}dx\end{align}
のように(分子の次数)\(\geqq \) (分母の次数)となっている分数式の積分では\(,\) まず分子を分母で割って分子の次数を落とすのが定石です.
\begin{align}=\sqrt{e}(1+\log{2})-2\sqrt{e}+2\cdot \frac{\sqrt{e}}{4}\pi -\frac{\sqrt{e}}{2}-\sqrt{e}\log{2}\end{align}
\begin{align}=\frac{\sqrt{e}}{2}\pi -\frac{3}{2}\sqrt{e}=\frac{\sqrt{e}}{2}(\pi -3)~~~~\cdots \fbox{答}\end{align}
(え)\(\displaystyle \frac{\sqrt{e}}{2}(\pi -3)\)






コメント