理学部第二部(数学科専用問題)2023年第3問の問題文全文
\(a\) を \(0<a<1\) を満たす実数とし\(,\) \(f(x)=(1-a)x^2(x-a)\) とする. このとき\(,\) 以下の問いに答えよ.
(1) 関数 \(f(x)\) の増減を調べよ. また\(,\) そのグラフの概形をかけ.
(2) 曲線 \(y=f(x)\) と \(x\) 軸で囲まれた部分の面積 \(S(a)\) を求めよ.
(3) 曲線 \(y=f(x)\) と \(x\) 軸で囲まれた部分を \(x\) 軸のまわりに一回転してできる回転体の体積 \(V(a)\) を求めよ.
(4) \(a\) が \(0<a<1\) の範囲を動くとき\(,\) \(\displaystyle \frac{V(a)}{S(a)}\) の最大値を求めよ.
(1) の解答〜\(1-a\) の符号に注意〜
\begin{align}f^{\prime}(x)=(1-a)\{2x(x-a)+x^2\}\end{align}
\begin{align}=(1-a)x(3x-2a)\end{align}
増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline x & \cdots & 0 & \cdots & \displaystyle \frac{2}{3}a & \cdots \\ \hline f^{\prime}(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & 0 & \searrow & \displaystyle -\frac{4}{27}(1-a)a^3 & \nearrow \\ \hline \end{array}\end{align}
増減表よりグラフの概形は以下のようになる.
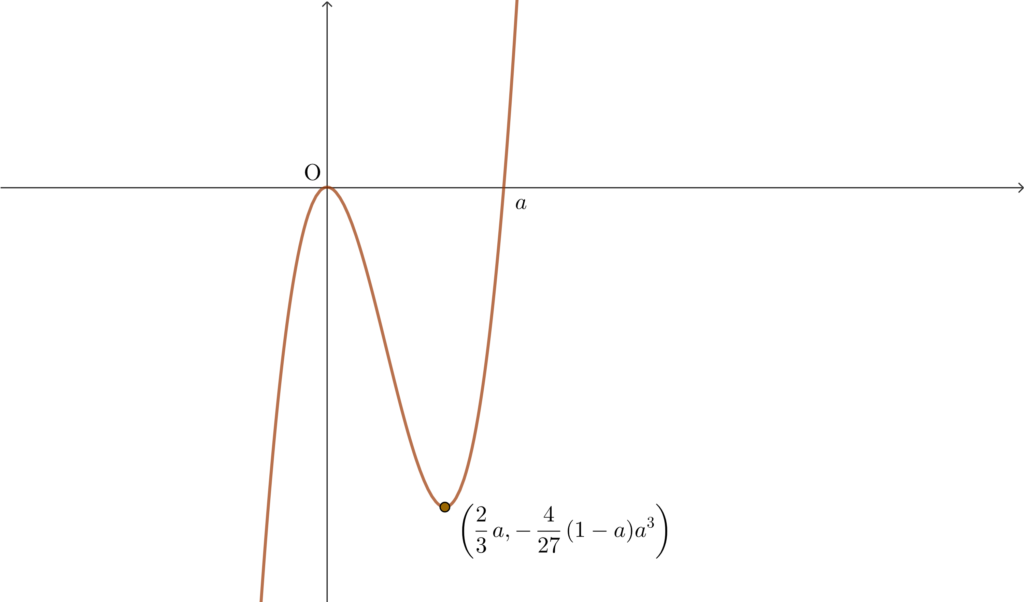
(2) の解答〜\(\displaystyle \frac{1}{12}\) 公式で瞬殺〜
\(\displaystyle \frac{1}{12}\) 公式とは?
\(3\) 次関数と接線で囲まれる部分の面積については \(\displaystyle \frac{1}{12}\) 公式を使って求めることができます. 参考URLをつけているので忘れた方や知らない方は参考にしてみてください. (「高校数学の美しい物語」さんはブログでの無断使用OKと明記されているので使用させていただきました.)
https://manabitimes.jp/math/796
\(\displaystyle \frac{1}{12}\) 公式を使って \(S(a)\) を求める
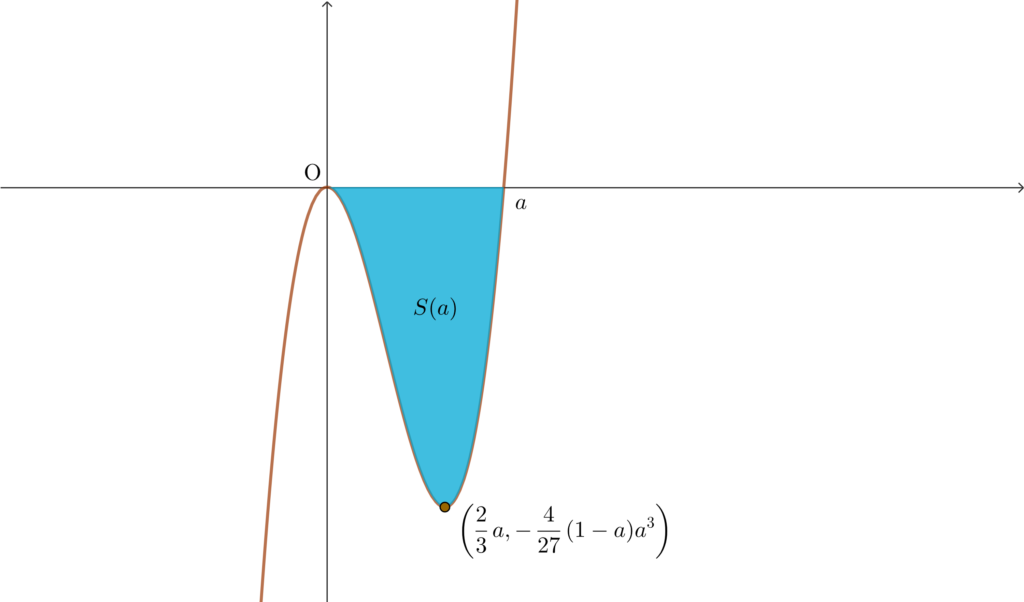
\begin{align}S(a)=\int_0^a -(1-a)x^2(x-a)dx\end{align}
\begin{align}=\frac{(1-a)a^4}{12}~~~~\cdots \fbox{答}\end{align}
(3) の解答〜回転体の体積は \(\pi y^2\) の積分〜
\begin{align}V(a)=\pi \int_0^a\{(1-a)x^2(x-a)\}^2dx\end{align}
\begin{align}=(1-a)^2\pi \int_0^a(x^6-2ax^5+a^2x^4)dx\end{align}
\begin{align}=(1-a)^2\pi \biggl[\frac{1}{7}x^7-\frac{a}{3}x^6+\frac{a^2}{5}x^5\biggr]_0^a\end{align}
\begin{align}=(1-a)^2\pi \left(\frac{a^7}{7}-\frac{a^7}{3}+\frac{a^7}{5}\right)\end{align}
\begin{align}=(1-a)^2\pi \cdot \frac{15-35+21}{105}a^7\end{align}
\begin{align}=\frac{(1-a)^2a^7}{105}\pi~~~~\cdots \fbox{答}\end{align}
(4) の解答〜計算ミスのないように丁寧に〜
\begin{align}g(a)=\frac{V(a)}{S(a)}\end{align}
\begin{align}=\frac{(1-a)^2a^7}{105}\pi \cdot \frac{12}{(1-a)a^4}\end{align}
\begin{align}=\frac{4\pi}{35}(1-a)a^3\end{align}
\begin{align}g^{\prime}(a)=\frac{4\pi}{35}\{-a^3+(1-a)\cdot 3a^2\}\end{align}
\begin{align}=\frac{4\pi}{35}a^2(3-4a)\end{align}
\(\displaystyle \frac{4\pi}{35}a^2>0\) であるから\(,\) \(3-4a\) の符号と \(g^{\prime}(a)\) の符号は一致する. よって\(,\) 増減表は以下のようになる.
\begin{align}\begin{array}{|c|c|c|c|c|c|}\hline a & 0 & \cdots & \displaystyle \frac{3}{4} & \cdots & 1 \\ \hline g^{\prime}(a) & {} & + & 0 & – & {} \\ \hline g(a) & 0 & \nearrow & 最大 & \searrow & 0 \\ \hline \end{array}\end{align}
増減表より\(,\) 最大値は
\begin{align}g\left(\frac{3}{4}\right)=\frac{4\pi}{35}\cdot \frac{1}{4}\cdot \frac{27}{64}=\frac{27}{2240}\pi~~~~\cdots \fbox{答}\end{align}





コメント