理学部第二部2020年第６問

理【二部】

2020.07.25

(3)は $\frac{1}{12}$ 公式を使えば瞬殺です. 穴埋め式なので積極的に使いたいところです.

問題文全文
(1) の解答
(2) の解答
(3) の解答（穴埋め問題として）
(3) の解答（記述式の場合）

問題文全文

$a, b$ を実数とする. 座標平面上で, 曲線 $y=x^2+2x-3$ を $C_1$ とし, 曲線 $y=(x+a)^2+b$ を $C_2$ とする. $C_2$ は 2 点 $\mathrm{A}(1, 9)$ と $\mathrm{B}(5, 17)$ を通る. また, 直線 $\ell$ は $C_1$ と $C_2$ の両方に接しているとする.

(1) $a=-\fbox{$\hskip0.8emの\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$},~~b=\fbox{$\hskip0.8emは\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ である. また, $C_1$ と $C_2$ の交点の $x$ 座標は $\displaystyle \frac{\fbox{$\hskip0.8emひ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emふ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}$ である.

(2) 直線 $\ell$ の方程式は $y=\fbox{$\hskip0.8emへ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}x-\fbox{$\hskip0.8emほ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ である. また, $C_1$ と $\ell$ との接点の $x$ 座標は $\fbox{$\hskip0.8emみ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}$ である.

(3) 2 つの曲線 $C_1,~C_2$ と直線 $\ell$ によって囲まれた部分の面積は $\displaystyle \frac{\fbox{$\hskip0.8emむ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emめ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}$ である.

(1) の解答

$C_2$ は 2 点 $\mathrm{A}(1, 9),~~\mathrm{B}(5, 17)$ を通るので

\begin{align}\left\{\begin{array}{l}9=(1+a)^2+b \\ 17=(5+a)^2+b \\ \end{array}\right.\end{align}

これを解いて, $a=-2, b=8$

quandle

$b$ の係数が揃ってるので, そのまま辺々を引きます. すると右辺が（２乗）ー（２乗）の形になるので, 和と差の積に因数分解できます.

つまり

\begin{align}8=(5+a)^2-(1+a)^2\Leftrightarrow 8=(2a+6)\cdot 4\end{align}

となるので両辺を 8 で割ればすぐに $a$ の値が求まります.

このとき, $C_2~:~y=(x-2)^2+8=x^2-4x+12$ となる. $C_1$ と $C_2$ の交点の $x$ 座標は $x^2+2x-3=x^2-4x+12$ の解であるから, これを解くと, $\displaystyle x=\frac{5}{2}$ を得る.

(2) の解答

$C_1$ と $\ell$ の接点を $(s, s^2+2s-3)$ とおくと, $y^{\prime}=2x+2$ より, 直線 $\ell$ の方程式は

\begin{align}y=(2s+2)(x-s)+s^2+2s-3\Leftrightarrow y=(2s+2)x-s^2-3~~\cdots ①\end{align}

となる. 一方, $C_2$ と $\ell$ の接点を $(t, t^2-4t+12)$ とおくと, $y^{\prime}=2x-4$ より, 直線 $\ell$ の方程式は

\begin{align}y=(2t-4)(x-t)+t^2-4t+12\Leftrightarrow y=(2t-4)x-t^2+12\cdots ②\end{align}

①と②は一致するので

\begin{align}\left\{\begin{array}{l}2s+2=2t-4 \\ -s^2-3=-t^2+12 \\ \end{array}\right.\end{align}

これを解いて, $s=1,~t=4$ を得る. よって, $C_1$ と $\ell$ の接点の $x$ 座標は 1, $C_2$ と $\ell$ の接点の $x$ 座標は 4 である.

(3) の解答（穴埋め問題として）

quandle

今回は穴埋め式の問題ですから $\frac{1}{12}$ 公式を使えば瞬殺です. 実際の入試の時はこちらを使いましょう.

(2) より, $C_1$ と $\ell$ の接点の $x$ 座標は 1, $C_2$ と $\ell$ の接点の $x$ 座標は 4 であるから, 求める面積は

\begin{align}\frac{1}{12}(4-1)^3=\frac{27}{12}=\frac{9}{4}.\end{align}

(3) の解答（記述式の場合）

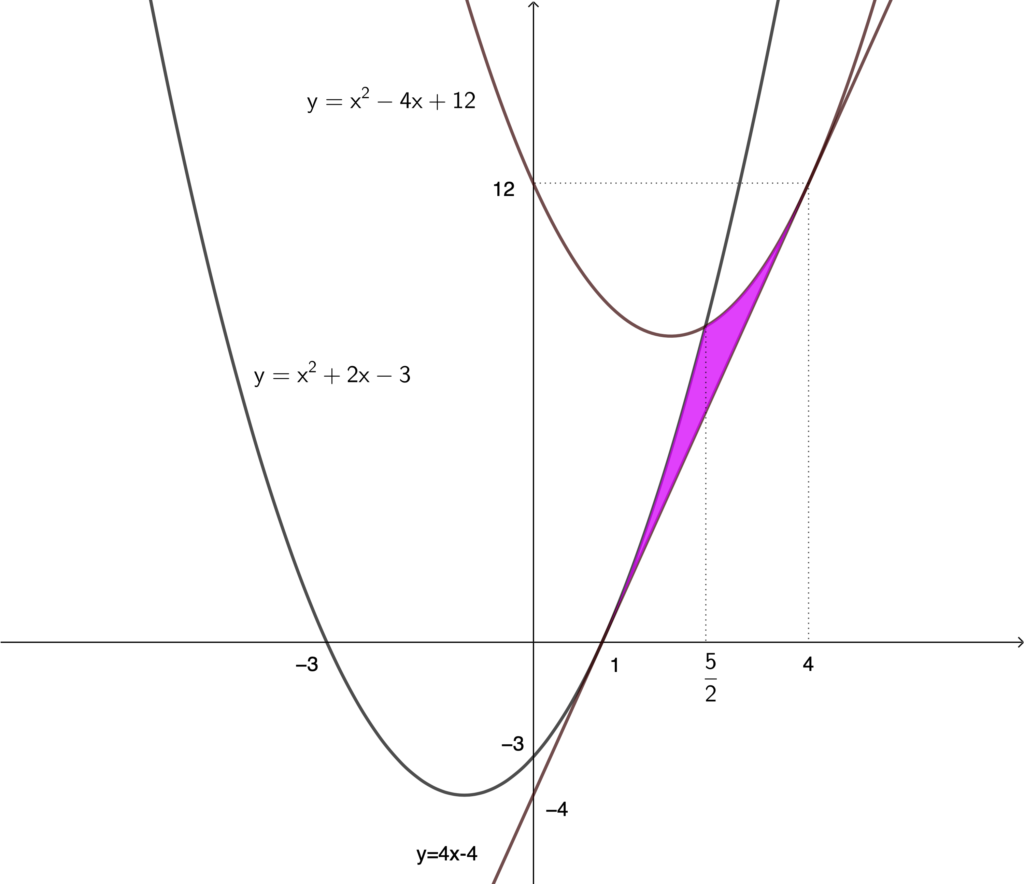
求める面積は上図の斜線部分の面積である.

\begin{align}\int_1^{\frac{5}{2}}\left\{x^2+2x-3-(4x-4)\right\}dx+\int_{\frac{5}{2}}^4\left\{x^2-4x+12-(4x-4)\right\}dx\end{align}

\begin{align}=\int_{1}{\frac{5}{2}}(x-1)^2dx+\int_{\frac{5}{2}}^4(x-4)^2dx=\biggl[\frac{1}{3}(x-1)^3\biggr]_1^{\frac{5}{2}}+\biggl[\frac{1}{3}(x-4)^3\biggr]_{\frac{5}{2}}^4\end{align}

\begin{align}=\frac{9}{8}+\frac{9}{8}=\frac{9}{4}.\end{align}