問題文全文
自然数 \(n\) に対して\(,\) 関数 \(f_n(x),~g_n(x)\) を
\begin{align}f_n(x)=2\left(\frac{x}{2}\right)^{-\frac{1}{n}},~g_n(x)=2\left(\frac{x}{2}\right)^{-n}~~(x>0)\end{align}
と定める. また\(,\) 座標平面において\(,\) 原点を中心とする半径 \(r_n\) の円 \(C_n\) が\(,\) 曲線 \(y=f_n(x),~y=g_n(x)\) のそれぞれと\(,\) 第一象限においてただ 1 つの共有点をもつとする.
(1) 円 \(C_1\) と曲線 \(y=f_1(x)\) の共有点の座標は\(,\) \(\left(\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}, ~\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)\) である.
(2) \(n\geqq 2\) とする. このとき\(,\) 2 曲線 \(y=f_n(x),~y=g_n(x)\) はただ 1 つの共有点をもち\(,\) その座標は \(\left(\fbox{$\hskip0.8emウ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}, ~\fbox{$\hskip0.8emエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\right)\) である.
(3) \(r_2=2^{\frac{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emカ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}}\sqrt{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) をとる.
(4) \(n\) が自然数全体を動くとき\(,\) \(r_n\) は\(,\) \(n=\fbox{$\hskip0.8emク\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\)のとき\(,\) 最大値 \(\fbox{$\hskip0.8emケ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\) をとる.
(5) \(n\geqq 2\) のとき\(,\) 円 \(C_n\) と 2 曲線 \(y=f_n(x),~ y=g_n(x)\) で囲まれた図形の面積を\(S_n\) とする. このとき\(,\) \(\displaystyle \lim_{n\rightarrow \infty}\frac{\log n}{n}=0\) ということなどから\(,\)
\begin{align}\lim_{n\rightarrow \infty}S_n=\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}-\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\pi\end{align}
であることがわかる.
(1) の着眼点
共有点の座標と言われているので\(,\) ノータイムで連立方程式を解きたくなりますが\(,\) 連立した後の式が4次式になるので抵抗があります.
\(C_1~:~x^2+y^2=r_1^2\) と \(\displaystyle f_1(x)=\frac{4}{x}\) つまり \(xy=4\) はどちらも \(x,~y\) の対称式になっています. つまり\(,\) どちらも \(y=x\) 対称なグラフです.
\(C_1\) も \(y=f_1(x)\) も第 1 象限では \(y=x\) と共有点を 1 つだけ持つので\(,\) \(C_1\) と \(y=f_1(x)\) が共有点を 1 つしか持たないのであれば一致するはずです.
\(y=x\) との共有点を考えるのは \(y=f(x)\) とその逆関数 \(y=f^{-1}(x)\) の共有点を求めるときには特に有効です.
(1) の解答
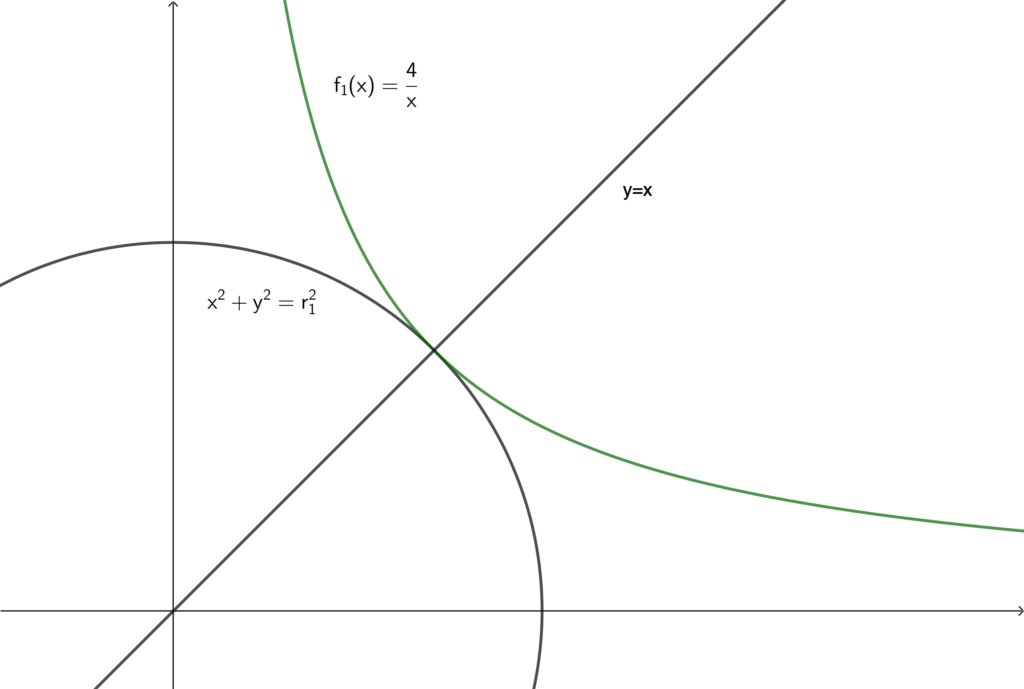
\begin{align} C_1~:~x^2+y^2=r_1^2,~~f_1(x)=2\cdot \left(\frac{x}{2}\right)^{-1}=\frac{4}{x}\end{align}
はどちらも直線 \(y=x\) に関して対称なグラフである. \(C_1\) と \(y=f_1(x)\) はただ一つの共有点をもち\(,\) かつ\(,\) 第 1 象限においては \(C_1\) と \(y=f_1(x)\) は共に \(y=x\) と共有点を 1 つだけ持つのでこれらはすべて一致する.
よって\(,\) 求める共有点は \(\displaystyle y=\frac{4}{x}\) と \(y=x\) の共有点に一致する.
\(x>0\) において \(\displaystyle x=\frac{4}{x}\) より\(,\) \(x=2\)
求める共有点は \((2,~2)\).
(2) の解答
\begin{align}2\cdot \left(\frac{x}{2}\right)^{-\frac{1}{n}}=2\cdot \left(\frac{x}{2}\right)^{-n}\end{align}
のとき\(,\) \(n\geqq 2\) より\(,\) \(\displaystyle -\frac{1}{n}\neq -n\) であるから\(,\) 等号が成立するのは
\begin{align}\frac{x}{2}=1\end{align}
のときのみである. よって\(,\) 共有点の座標は
\begin{align}\left(2,~2\cdot \left(\frac{2}{2}\right)^{-\frac{1}{n}}\right)=(2,~2).\end{align}
(3) の着眼点
条件より\(,\) \(y=g_2(x)\) と \(C_2\) はある 1 点で接しています. 2 曲線が接するというのは\(,\) その点において共通接線を持つということです.
\(\displaystyle g_2(x)=\frac{8}{x^2}\) 上の点 \(\displaystyle \left(t,~\frac{8}{t^2}\right)\) における接線は微分を利用して求めることができます. 出てくる接線は \(t\) を用いて表されます.
一方\(,\) \(x^2+y^2=r_2^2\) 上の点 \((r_2\cos \theta,~r_2\sin \theta)\) における接線は円の接線の公式からすぐに求めることができます. 出てくる接線は \(r_2\) と \(\theta\) を用いて表されます.
未知数 \(t,~r_2,~\theta\) の 3 つに対して式が二つ立ちました. 最後の 1 個は接点が共通ということから \(\displaystyle \left(t,~\frac{8}{t^2}\right)=(r_2\cos \theta,~r_2\sin \theta)\) という関係式が作れます. これで未知数の数と式の数が一致しました.
(3) の解答
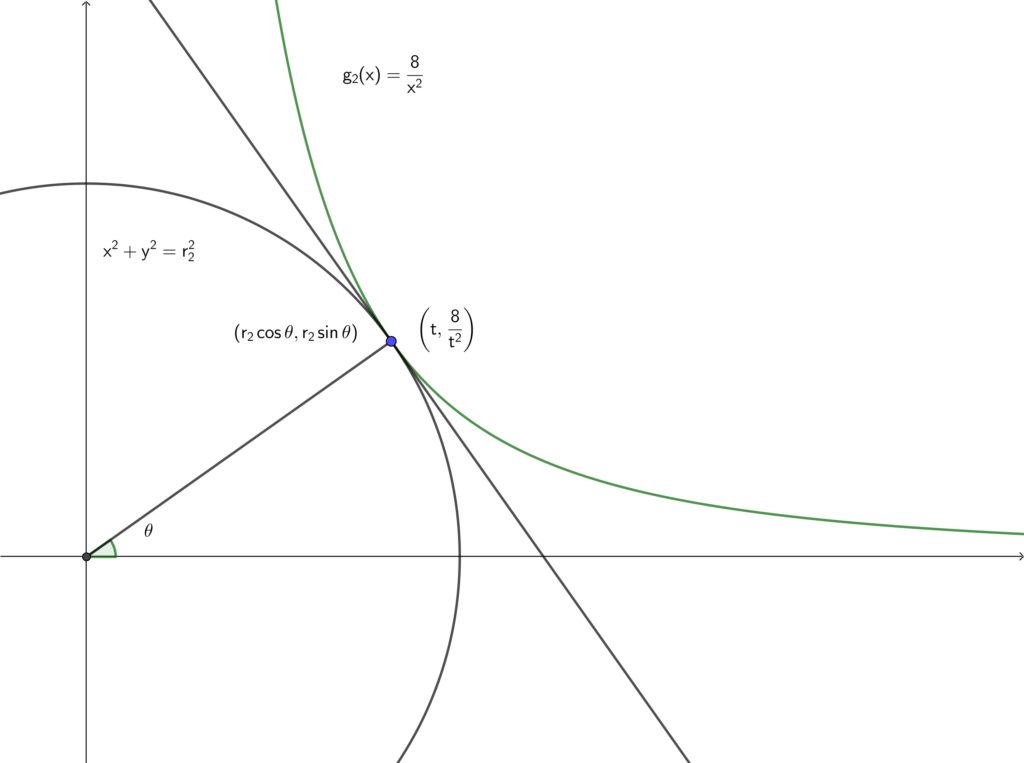
\(C_2\) と \(\displaystyle g_2(x)=2\cdot \left(\frac{x}{2}\right)^{-2}=\frac{8}{x^2}\) の共有点を \(\mathrm{P}_2\) とおく.
まず\(,\) \(\displaystyle g_2(x)=\frac{8}{x^2}\) 上の点 \(\displaystyle \mathrm{P}_2\left(t,~\frac{8}{t^2}\right)\) における接線を求める.
\(\displaystyle g_2^{\prime}(x)=-\frac{16}{x^3}\) より接線は
\begin{align}y=-\frac{16}{t^3}(x-t)+\frac{8}{t^2}\end{align}
\begin{align}y=-\frac{16}{t^3}x+\frac{24}{t^2}\end{align}
\begin{align}16x+t^3y-24t=0~~~~\cdots ①\end{align}
次に\(,\) \(C_2\) 上の点 \(\mathrm{P}_2(r_2\cos \theta,~r_2\sin \theta)\) における接線を求めると\(,\)
\begin{align}(r_2\cos \theta)x+(r_2\sin \theta)y=r_2^2~~~~\cdots ②\end{align}
① と ② は一致するので\(,\)
\begin{align}\frac{t^3}{16}=\frac{r_2\sin \theta}{r_2\cos \theta}\end{align}

quandle
直線が一致するということは\(,\) 傾きが等しいということです.
傾きが等しいということは \(x\) の係数と \(y\) の係数の比が等しいということです.
\begin{align}\tan \theta=\frac{t^3}{16}~~~~\cdots ③\end{align}
また接点 \(\mathrm{P}_2\) も一致するため\(,\)
\begin{align}t=r_2\cos \theta,~\frac{8}{t^2}=r_2\sin \theta~~~~\cdots ④\end{align}
であることから\(,\) 辺々割り算して\(,\)
\begin{align}\frac{r_2\sin \theta}{r_2\cos \theta}=\cfrac{\cfrac{8}{t^2}}{t}\end{align}
\begin{align} \tan \theta =\frac{8}{t^3}~~~~\cdots ⑤\end{align}
③ ⑤より
\begin{align}\frac{8}{t^3}=\frac{t^3}{16}\end{align}
\begin{align}t^6=2^7\end{align}
\begin{align}t=2^{\frac{7}{6}}\end{align}
④ に代入して\(,\)
\begin{align}r_2\cos \theta =2^{\frac{7}{6}},~r_2\sin \theta =\frac{2^3}{2^{\frac{7}{3}}}=2^{\frac{2}{3}}\end{align}
\begin{align}\sin \theta =\frac{2^{\frac{2}{3}}}{r_2},~\cos \theta =\frac{2^{\frac{7}{6}}}{r_2}\end{align}
\(\sin^2{\theta}+\cos^2{\theta}=1\) より
\begin{align}\frac{2^{\frac{4}{3}}}{r_2^2}+\frac{2^{\frac{7}{3}}}{r_2^2}=1\end{align}
\begin{align}r_2^2=2^{\frac{4}{3}}+2^{\frac{7}{3}}=(1+2)\cdot 2^{\frac{4}{3}}=3\cdot 2^{\frac{4}{3}}\end{align}
よって\(,\)
\begin{align}r_2=2^{\frac{2}{3}}\cdot \sqrt{3}.\end{align}
(4) の解答

quandle
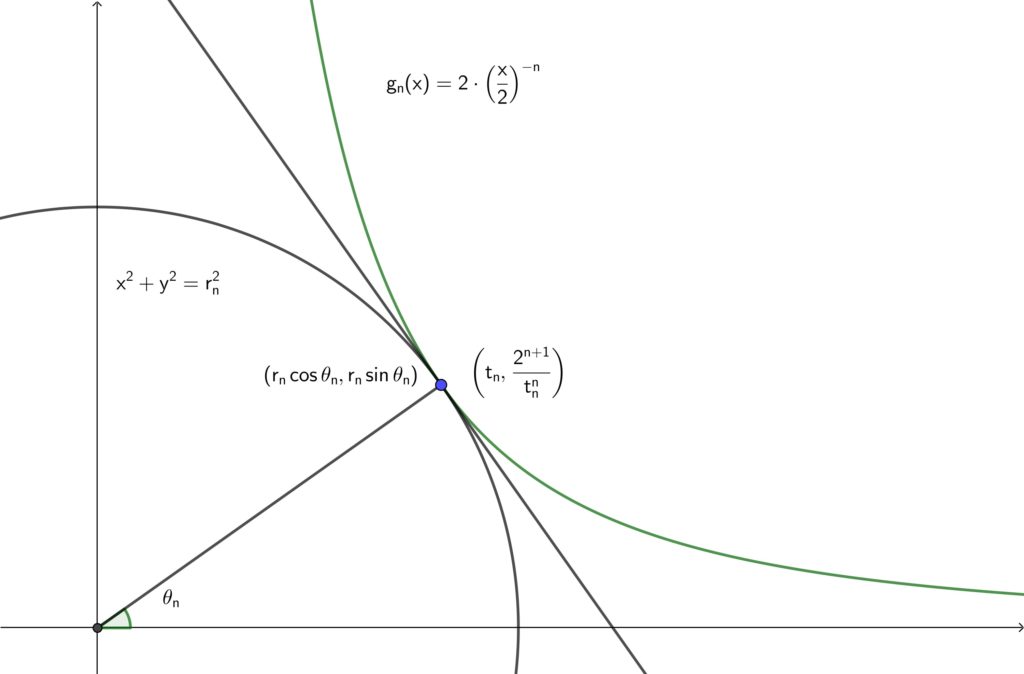
(3) でやったことを一般の場合でもやってみます. 変数を \(r_n,~t_n,~{\theta}_n\) に変えれば\(,\) まったく同じ流れで \(r_n\) が求まるはずです.
\(r_n\) は \(n\) の式でかけるはずですが\(,\) 現地点ではどんな形になるか見通しが立たないので\(,\) 一旦 \(r_n\) を出すことに注力します. 最大値をどうやって求めるかは形を見て再度考察することになります.
\begin{align}g_n^{\prime}(x)=-n\left(\frac{x}{2}\right)^{-n-1}\end{align}
より\(,\) \(y=g_n(x)\) 上の点 \(\displaystyle \mathrm{P}_n\left(t_n,~2\cdot \left(\frac{t_n}{2}\right)^{-n}\right)\) における接線は
\begin{align}y=-n\left(\frac{t_n}{2}\right)^{-n-1}(x-t_n)+2\cdot \left(\frac{t_n}{2}\right)^{-n}\end{align}
\begin{align}y=-n\left(\frac{t_n}{2}\right)^{-n-1}x+2(n+1)\cdot \left(\frac{2}{t_n}\right)^n~~~~\cdots(ア)\end{align}
\(C_n\) 上の点 \(\mathrm{P}_n(r_n\cos{\theta}_n,~r_n\sin{\theta}_n)\) における接線は
\begin{align}(r_n\cos{\theta}_n)x+(r_n\sin{\theta}_n)y=r_n^2~~~~\cdots (イ)\end{align}
(ア)と(イ)は一致するため
\begin{align}-\frac{r_n\cos{\theta}_n}{r_n\sin{\theta}_n}=-n\left(\frac{t_n}{2}\right)^{-n-1}\end{align}
\begin{align}\tan{\theta}_n=\frac{1}{n}\left(\frac{t_n}{2}\right)^{n+1}~~~~\cdots (ウ)\end{align}
また接点 \(\mathrm{P}_n\) も一致するため
\begin{align}r_n\cos{\theta}_n=t_n,~r_n\sin{\theta}_n=2\cdot \left(\frac{t_n}{2}\right)^{-n}~~~~\cdots (エ)\end{align}
\begin{align}\tan{\theta}_n=\cfrac{2\cdot \cfrac{2^n}{t_n^n}}{t_n}=\left(\frac{2}{t_n}\right)^{n+1}~~~~\cdots (オ)\end{align}
(ウ)と(オ)より
\begin{align}\left(\frac{2}{t_n}\right)^{n+1}=\frac{1}{n}\left(\frac{t_n}{2}\right)^{n+1}\end{align}
\begin{align}n\cdot 2^{2n+2}=t_n^{2n+2}\end{align}
\begin{align}\left(\frac{t_n}{2}\right)^{2n+2}=n\end{align}
\begin{align}t_n=2n^{\frac{1}{2n+2}}\end{align}
(エ)に代入して
\begin{align}r_n\cos{\theta}_n=2n^{\frac{1}{2n+2}},~r_n\sin{\theta}_n=2\left(\frac{2n^{\frac{1}{2n+2}}}{2}\right)^{-n}=2n^{-\frac{n}{2n+2}}\end{align}
\begin{align}\cos{\theta}_n=\frac{2n^{\frac{1}{2n+2}}}{r_n},~\sin{\theta}_n=\frac{2}{r_n\cdot n^{\frac{n}{2n+2}}}\end{align}
\(\sin^2{\theta}_n+\cos^2{\theta}_n=1\) より
\begin{align}\frac{4}{r_n^2\cdot n^{\frac{n}{n+1}}}+\frac{4n^{\frac{1}{n+1}}}{r_n^2}=1\end{align}
\begin{align}4+4n=n^{\frac{n}{n+1}}r_n^2\end{align}
\begin{align}r_n^2=\frac{4(n+1)}{n^{\frac{n}{n+1}}}\end{align}

quandle
\(r_n\) の最大値を考えたいです. よくある手法は\(\displaystyle \frac{r_{n+1}}{r_n}\) が 1 より大きくなる \(n\) を見つけるというものですが\(,\) やってみたところうまく行きそうにありませんでした.
そこで一旦整数ではなく実数に範囲を拡張することで関数とみることができ\(,\) 微分ができるようになります.
実数の範囲で最大値をとる \(x\) の値が出せればその周辺の自然数で最大値をとるはずという考え方です.
ここで実数 \(x\) に関する関数
\begin{align}h(x)=\frac{x+1}{x^{\frac{x}{x+1}}}\end{align}
について考える.

quandle
\(x^x\) のような「関数の関数乗」を微分したいときは対数微分法を利用しましょう!
\(x>0\) としてよい. このとき \(h(x)\) は明らかに正の値をとる.
\begin{align}\log{h(x)}=\log{(x+1)}-\frac{x}{x+1}\log x\end{align}
\begin{align}\frac{h^{\prime}(x)}{h(x)}=\frac{1}{x+1}-\left\{\frac{1}{(x+1)^2}\log x+\frac{1}{x+1}\right\}=-\frac{1}{(x+1)^2}\log x\end{align}
\begin{align}h^{\prime}(x)=-\frac{\log x}{x^{\frac{x}{x+1}}(x+1)}\end{align}
\begin{array}{c|c|c|c|c}x & 0 & \cdots & 1 & \cdots \\ \hline h^{\prime}(x) & {} & + & 0 & – \\ \hline h(x) & {} & \nearrow & 2 & \searrow \\ \end{array}
増減表より\(,\) \(x=1\) のとき \(h(x)\) は最大値 2 をとる.
このとき \(r_n\) も最大値をとるから\(,\) \(n=1\) のとき\(,\) 最大値 \(r_1=2\sqrt{2}\).

quandle
今回はたまたま \(h(x)\) の最大をとる \(x\) が整数値で出たのでそのまま \(r_n\) に代入すればいいのですが \(,\) もし \(x=\sqrt{3}\) で \(h(x)\) が最大をとった場合\(,\) \(r_n\) が最大になる \(n\) はどうなるでしょうか. \(\sqrt{3}\) に最も近い整数である \(n=1\) と \(n=2\) について \(r_n\) を求め\(,\) より大きい方が最大となります.
(5) の解答
\begin{align}(f_n\circ g_n)(x)=2\left\{\frac{2\cdot \left(\frac{x}{2}\right)^{-n}}{2}\right\}^{-\frac{1}{n}}=x\end{align}
\begin{align}(g_n\circ f_n)(x)=2\left\{\frac{2\cdot \left(\frac{x}{2}\right)^{-\frac{1}{n}}}{2}\right\}^{-n}=x\end{align}
より\(,\) \(y=f_n(x)\) と \(y=g_n(x)\) は互いに逆関数の関係になっているので\(,\) \(y=x\) に関して対称である. また\(,\) 円 \(C_n\) も \(y=x\) に関して対称であるから\(,\) 求める面積は上図の赤色部分である.
上図のように \(Q_n,~R_n,~T_n,~U_n\) をおく. また\(,\) \(y=g_n(x),\) 線分 \(\mathrm{R_nT_n},\) 線分 \(\mathrm{P_nQ_n},\) \(x\) 軸によって囲まれる部分の面積を \(A\) とする.
求める面積 \(S_n\) は
\begin{align}S_n=2(A+\triangle \mathrm{OR_nT_n}-~扇型~\mathrm{OU_nP_n}-\triangle \mathrm{OP_nQ_n})\end{align}
以下それぞれの項の面積を求めていく.
\begin{align}A=\int_2^{t_n}2\left(\frac{x}{2}\right)^{-n}dx\end{align}
\begin{align}=\biggl[\frac{4}{1-n}\left(\frac{x}{2}\right)^{1-n}\biggr]_2^{t_n}=\frac{4}{1-n}\left\{\left(\frac{t_n}{2}\right)^{1-n}-1\right\}\end{align}
\begin{align}=\frac{4}{1-n}\left\{\frac{t_n}{2}\cdot \frac{1}{2}\cdot 2\left(\frac{t_n}{2}\right)^{-n}-1\right\}=\frac{1}{n-1}(4-t_nu_n)\end{align}
\begin{align}\triangle \mathrm{OR_nT_n}=\frac{1}{2}\cdot 2\cdot 2=2\end{align}
\begin{align}扇型~\mathrm{OU_nP_n}=\frac{1}{2}r_n^2\left(\frac{\pi}{4}-\theta_n\right)\end{align}
\begin{align}\triangle \mathrm{OP_nQ_n}=\frac{1}{2}t_nu_n\end{align}
よって\(,\)
\begin{align}S_n=2\left\{\frac{1}{n-1}(4-t_nu_n)+2-\frac{1}{2}r_n^2\left(\frac{\pi}{4}-\theta_n\right)-\frac{1}{2}t_nu_n\right\}\end{align}
\begin{align}=\frac{2}{n-1}(4-t_nu_n)+4-r_n^2\left(\frac{\pi}{4}-\theta_n\right)-t_nu_n\end{align}
S_nの極限値を求めるための着眼点
\begin{align}r_n^2=t_n^2+u_n^2\end{align}
より\(,\) \(r_n\) は \(t_n\) と \(u_n\) で表されます.
\({\theta}_n\) を直接表すことは難しいですが\(,\) \(\tan{\theta}_n\) であれば\(,\)
\begin{align}\tan{\theta}_n=\frac{u_n}{t_n}\end{align}
とやはり \(t_n\) と \(u_n\) で表されています.
よって\(,\) \(S_n\) の極限値を求めるためには
\begin{align}\lim_{n\to \infty}t_n,~\lim_{n\to \infty}u_n\end{align}
が求められれば良いことがわかります.
\(t_n\) も \(u_n\) も関数の関数乗という形をしているので \(\log\) をとって極限をとると良いでしょう.
S_nの極限値以降の解答
\begin{align}\lim_{n\to \infty}\log{t_n}=\lim_{n\to \infty}\log{2n^{\frac{1}{2n+2}}}\end{align}
\begin{align}=\lim_{n\to \infty}\left(\log 2+\frac{1}{2n+2}\log n\right)=\lim_{n\to \infty}\left(\log 2+\frac{n}{2n+2}\cdot \frac{\log n}{n}\right)\end{align}
\begin{align}=\lim_{n\to \infty}\left(\log 2+\cfrac{1}{2+\cfrac{2}{n}}\cdot \frac{\log n}{n}\right)=\log 2\end{align}
よって\(,\)
\begin{align}\lim_{n\to \infty}t_n=2\end{align}
一方\(,\)
\begin{align}\lim_{n\to \infty}\log{u_n}=\lim_{n\to \infty}\log{\left(2n^{-\frac{n}{2n+2}}\right)}\end{align}
\begin{align}=\lim_{n\to \infty}\left(\log 2-\frac{n}{2n+2}\log n\right)=\lim_{n\to \infty}\left(\log 2-\cfrac{1}{2+\cfrac{2}{n}}\log n\right)=-\infty\end{align}
よって\(,\)
\begin{align}\lim_{n\to \infty}u_n=+0\end{align}
このとき\(,\)
\begin{align}\lim_{n\to \infty}r_n^2=\lim_{n\to \infty}(t_n^2+u_n^2)=2^2+0^2=4\end{align}
\begin{align}\lim_{n\to \infty}\tan{\theta}_n=\lim_{n\to \infty}\frac{u_n}{t_n}=\frac{0}{2}=0\end{align}
より\(,\)
\begin{align}\lim_{n\to \infty}{\theta}_n=0\end{align}
以上より\(,\)
\begin{align}\lim_{n\to \infty}S_n=\lim_{n\to \infty}\left\{\frac{2}{n-1}(4-t_nu_n)+4-r_n^2\left(\frac{\pi}{4}-{\theta}_n\right)-t_nu_n\right\}\end{align}
\begin{align}=0\cdot (4-2\cdot 0)+4-4\left(\frac{\pi}{4}-0\right)-2\cdot 0=4-\pi.\end{align}












コメント