問題文全文
関数 \(f(x)=\cos{2x}-3\sqrt{3}\cos x+4~~(~0\leqq x\leqq 2\pi~)\) を考える.
(1) \(f(x)\geqq 0\) となるような \(x\) の範囲は,
\begin{align}\frac{\fbox{$\hskip0.8emア\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emイ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}} \leqq x\leqq \frac{\fbox{$\hskip0.8emウエ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emオ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\end{align}
である.
(2) 曲線 \(y=f(x)\) と \(x\) 軸で囲まれた部分を, \(x\) 軸のまわりに 1 回転してできる立体の体積を \(V\) とすると,
\begin{align}V=\fbox{$\hskip0.8emカキ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}{\pi}^2+\frac{\fbox{$\hskip0.8emクケコ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\fbox{$\hskip0.8emサ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\sqrt{\fbox{$\hskip0.8emシ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\pi\end{align}
である.
(3) \(n\) を自然数とし,
\begin{align}g_n=\sum_{k=1}^nf\left(\frac{k}{12n}\pi\right)\end{align}
とおく. \(\displaystyle \sin\left(\frac{1}{12}\pi\right)=\frac{\fbox{$\hskip0.8emス\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{6}-\fbox{$\hskip0.8emセ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{2}}{4}\) であるから,
\begin{align}\lim_{n\to \infty}\frac{g_n}{n}=\frac{\fbox{$\hskip0.8emソ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}{\pi}\left(\fbox{$\hskip0.8emタ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}+\fbox{$\hskip0.8emチ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emツ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}-\fbox{$\hskip0.8emテ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\sqrt{\fbox{$\hskip0.8emト\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}}\right)+\fbox{$\hskip0.8emナ\hskip0.8em\Rule{0pt}{0.8em}{0.4em}$}\end{align}
となる.
(1) の解答
\begin{align}\cos{2x}-3\sqrt{3}\cos x+4\geqq 0\end{align}
\begin{align}\Leftrightarrow 2\cos^2x-3\sqrt{3}\cos x +3\geqq 0\end{align}
\begin{align}\Leftrightarrow (\cos x-\sqrt{3})(2\cos x-\sqrt{3})\geqq 0\end{align}
\(-1\leqq \cos x\leqq 1\) より, \(\cos x-\sqrt{3}<0\) であるから,
\begin{align}2\cos x-\sqrt{3}\leqq 0\Leftrightarrow \cos x\leqq \frac{\sqrt{3}}{2}\Leftrightarrow \frac{\pi}{6}\leqq x\leqq \frac{11}{6}\pi.\end{align}

quandle
\(\cos x-\sqrt{3}<0\) であることを利用して両辺を割っています. 0 でないと断言できるものはどんどん割ってしまいましょう.
(2) の着眼点
① 体積を求めるのに、必ずしも正確なグラフは必要ありません. 今回の場合曲線と \(x\) 軸で囲まれる部分さえわかれば積分計算ができます.
② (1) の結果から\(\displaystyle\frac{\pi}{6}\leqq x\leqq \frac{11}{6}\pi\) に対して回転体の体積公式に代入すれば求められます.
③ \(\cos{2x}\) が周期 \(\pi\), \(\cos x\) が周期 \(2\pi\) なので, その和である \(f(x)\) の周期は \(2\pi\) になります. \(\displaystyle \frac{11\pi}{6}-\frac{\pi}{6}=\frac{5\pi}{3}\) ですから, 定義域内に一つの山ができるグラフになることが予想されます.
④ ③の山は対称性がある三角関数の和によってできているので対称性があると思われます. 恐らく \(\displaystyle \frac{\pi}{6}\) と \(\displaystyle \frac{11\pi}{6}\) の中点である \(x=\pi\) が対称な軸になるはずです. まずはそれを示しましょう.
⑤ ④であることを示すには, \(f(x-\pi)=f(x+\pi)\) を示せばいいです.これが示せれば求める体積は \(\displaystyle \frac{\pi}{6}\) から \(\pi\) までを積分したものを 2 倍すればいいことになります. 代入するものが \(\pi\) に変わるので計算も楽になります.
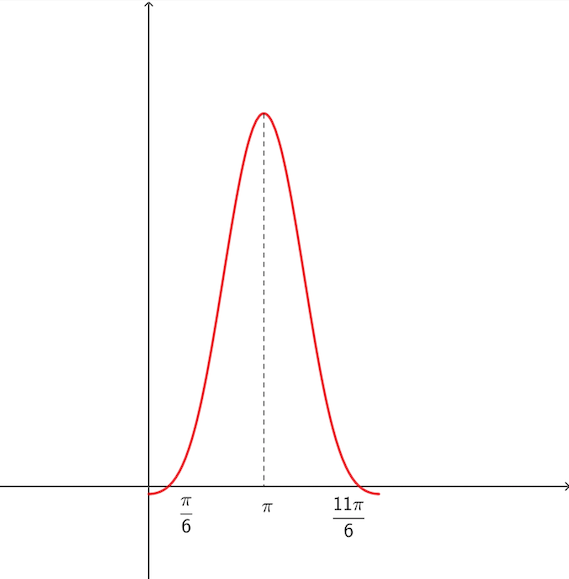
参考までにグラフは以下のようになります.
(2) の解答
(1) より, \(\displaystyle\frac{\pi}{6}\leqq x\leqq \frac{11}{6}\pi\) において \(f(x)\geqq 0\) であるから, \(\displaystyle\frac{\pi}{6}\leqq x\leqq \frac{11}{6}\pi\) における \(f(x)\) のグラフを \(x\) に関して 1 回転させればよい.
ここで,
\begin{align}f(\pi-x)=\cos{2(\pi-x)}-3\sqrt{3}\cos{(\pi-x)}+4=\cos{2x}+3\sqrt{3}\cos x+4\end{align}
\begin{align}f(\pi+x)=\cos{2(\pi+x)}-3\sqrt{3}\cos{(\pi+x)}+4=\cos{2x}+3\sqrt{3}\cos x+4\end{align}
であるから, \(f(x)\) は \(x=\pi\) に関して対称なグラフである. よって求める体積 \(V\) は,
\begin{align}V=2\pi\int_{\frac{\pi}{6}}^{\pi}\{f(x)\}^2dx=2\pi\int_{\frac{\pi}{6}}^{\pi}(\cos{2x}-3\sqrt{3}\cos x+4)^2dx\end{align}
\begin{align}=2\pi\int_{\frac{\pi}{6}}^{\pi}(\cos^2{2x}+27\cos^2x+16-6\sqrt{3}\cos{2x}\cos x-24\sqrt{3}\cos x+8\cos{2x})dx\end{align}
\begin{align}=2\pi\int_{\frac{\pi}{6}}^{\pi}\left\{\frac{1+\cos{4x}}{2}+27\cdot \frac{1+\cos{2x}}{2}+16-3\sqrt{3}\cos{3x}\cos x-24\sqrt{3}\cos x+8\cos{2x}\right\}dx\end{align}
\begin{align}=2\pi\int_{\frac{\pi}{6}}^{\pi}\left(\frac{1}{2}\cos{4x}-3\sqrt{3}\cos{3x}+\frac{43}{2}\cos{2x}-27\sqrt{3}\cos x+30\right)dx\end{align}
\begin{align}=2\pi\biggl[\frac{1}{8}\sin{4x}-\sqrt{3}\sin{3x}+\frac{43}{4}\sin{2x}-27\sqrt{3}\sin x+30x\biggr]_{\frac{\pi}{6}}^{\pi}\end{align}
\begin{align}=2\pi\left\{30\pi-\left(\frac{\sqrt{3}}{16}-\sqrt{3}+\frac{43\sqrt{3}}{8}-\frac{27\sqrt{3}}{2}+5\pi\right)\right\}\end{align}
\begin{align}=2\pi\left(\frac{145\sqrt{3}}{16}+25\pi\right)=50{\pi}^2+\frac{145\sqrt{3}}{8}\pi.\end{align}
(3) の解答
加法定理より
\begin{align}\sin{\frac{\pi}{12}}=\sin{\left(\frac{\pi}{3}-\frac{\pi}{4}\right)}=\frac{\sqrt{3}}{2}\cdot \frac{\sqrt{2}}{2}-\frac{1}{2}\cdot \frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}.\end{align}
\begin{align}\lim_{n\to \infty}\frac{g_n}{n}=\lim_{n\to \infty}\frac{1}{n}\sum_{k=1}^nf\left(\frac{k}{12n}\pi\right)\end{align}

quandle
区分求積法の形をしていますね. ちなみに公式は
\begin{align}\lim_{n\to \infty}\frac{1}{n}\sum_{k=1}^nf\left(\frac{k}{n}\right)=\int_0^1f(x)dx\end{align}
です. 代入して計算するだけです.
\begin{align}=\int_0^1f\left(\frac{\pi}{12}x\right)dx=\int_0^1\left(\cos{\frac{\pi}{6}x}-3\sqrt{3}\cos{\frac{\pi}{12}x}+4\right)dx\end{align}
\begin{align}=\biggl[\frac{6}{\pi}\sin{\frac{\pi}{6}x}-\frac{36\sqrt{3}}{\pi}\sin{\frac{\pi}{12}x}+4x\biggr]_0^1=\frac{3}{\pi}-\frac{36\sqrt{3}}{\pi}\cdot \frac{\sqrt{6}-\sqrt{2}}{4}+4\end{align}
\begin{align}=\frac{3}{\pi}(1+3\sqrt{6}-9\sqrt{2})+4.\end{align}






コメント