2月3日に理工学部(数学科・物理学科・情報科学科・応用生物学科・経営工学科)の入試が行われました. 受験された方お疲れ様でした.
微積分以外の解答速報はtwitterにアップしていますのでよろしければ下記からご覧ください.
問題文全文
\(e\) を自然対数の底とし\(,\) \(f(x)=xe^{-2x}\) とおく. \(\mathrm{O}\) を原点とする座標平面上の曲線 \(y=f(x)\) を \(C\) とおく. \(C\) 上の点 \((t,~f(t))\) における接線の傾きを \(a(t)\) とおく.
(1) \(a(t)\) を求めよ.
\(a(t)\) が最小となるときの \(t\) を \(t_1\) とおく.
(2) \(t_1\) を求めよ.
\(C\) 上の点 \(\mathrm{P}(t_1,~f(t_1))\) における法線を \(\ell\) とおく. \(\ell\) と \(x\) 軸の交点を \(\mathrm{Q}\) とおく.
(3) \(\mathrm{Q}\) の \(x\) 座標を求めよ.
(4) 線分 \(\mathrm{OQ},~\mathrm{QP}\) および曲線 \(C\) で囲まれた部分の面積を求めよ.

入試基礎レベルです. 言われている通りに計算すればいいので\(,\) 今回は着眼点は特にありません.
(1) の解答
(2) の解答
\(4e^{-2t}>0\) であるから\(,\) \(a^{\prime}(t)\) の符号は \(t-1\) の符号だけで決まる.
よって増減表は以下のようになる.
\begin{array}{c|c|c|c} t & \cdots & 1 & \cdots \\ \hline a^{\prime}(t) & – & 0 & + \\ \hline a(t) & \searrow & 最小 & \nearrow \end{array}
増減表より\(,\)
(3) の解答
\(f^{\prime}(1)=-e^{-2}\) より\(,\)
\(y=0\) のとき\(,\)
よって\(,\) \(\mathrm{Q}\) の \(x\) 座標は
(4) の解答
\(a^{\prime}(t)=f^{\prime\prime}(t)\) であるから\(,\) (2) により\(,\)
\(e^{-2x}>0\) であるから\(,\) \(f^{\prime}(x)\) の符号は \(1-2x\) の符号だけで決まり\(,\) \(f^{\prime\prime}(x)\) の符号は (2) の \(a^{\prime}(t)\) の符号に一致するから\(,\) 増減表は以下のようになる.
\begin{array}{c|c|c|c|c|c}x & \cdots & \displaystyle \frac{1}{2} & \cdots & 1 & \cdots \\ \hline f^{\prime}(x) & + & 0 & – & – & – \\ \hline f^{\prime\prime}(x) & – & – & – & 0 & + \\ \hline f(x) & \cap \nearrow & \displaystyle \frac{1}{2e} & \cap \searrow & \displaystyle \frac{1}{e^2} & \cup \searrow\end{array}

解説なので凹凸や極限まで調べてますが\(,\) 実際は面積を求めるだけなので凹凸も極限も不要です.
よって\(,\) グラフは以下のようになる.
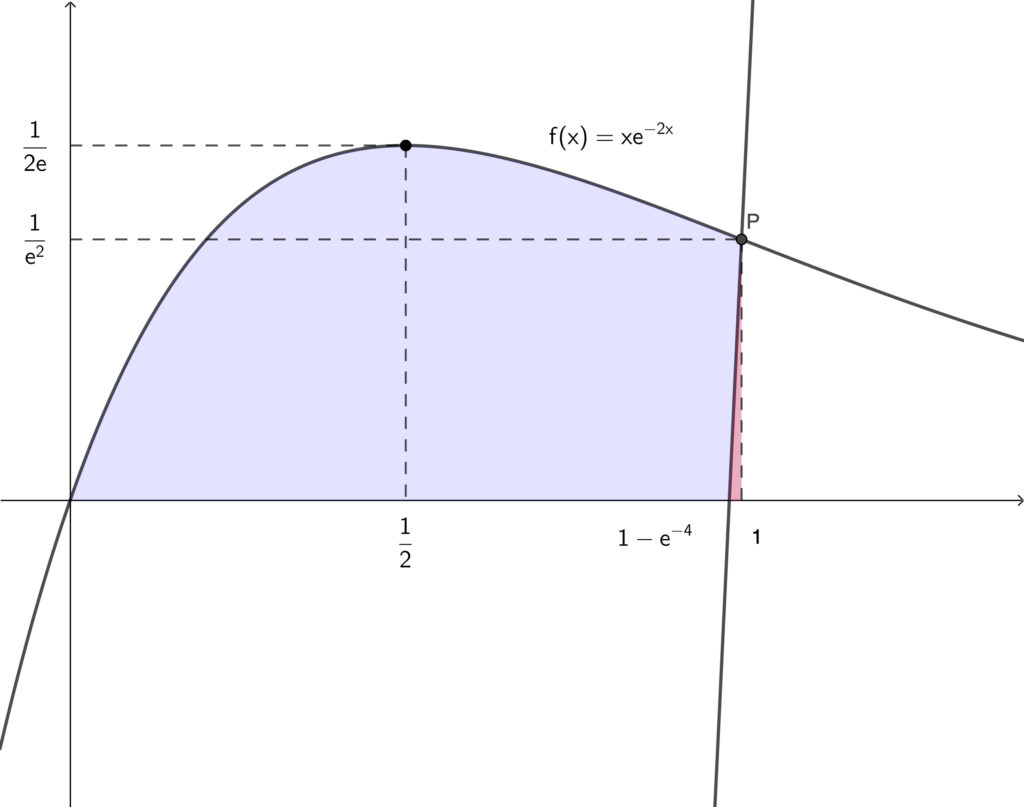
求める面積 \(S\) は


2021年第3問-120x68.jpg)

コメント