問題文全文
定数 \(a\) に対し\(,\)
\begin{align}f(x)=a\sin{2x}-\tan{x}~~\left(0\leqq x < \frac{\pi}{2}\right)\end{align}
とおく.
(1) \(\displaystyle a>\frac{1}{2}\) であるとする. 実数 \(\theta\) を\(,\) \(\displaystyle 0 < \theta < \frac{\pi}{2}\) かつ \(f(\theta)=0\) を満たすものとするとき\(,\) \(\cos{\theta}\) を \(a\) を用いて表せ.
(2) 不定積分
\begin{align}\int f(x)dx\end{align}
を求めよ.
(3) \(\displaystyle \frac{1}{2}< a<1\) であるとする. このとき\(,\)
\begin{align}\int_0^{\frac{\pi}{4}}|f(x)|dx+\log{a}\end{align}
を \(a\) の \(1\) 次式で表せ. ただし\(,\) \(\log\) は自然対数を表す.
(1) の解答
\begin{align}a\sin{2\theta}-\tan{\theta}=0\end{align}
\begin{align}2a\sin{\theta}\cos{\theta}-\frac{\sin{\theta}}{\cos{\theta}}=0\end{align}
\begin{align}\sin{\theta}(2a\cos^2{\theta}-1)=0\end{align}
\(\displaystyle 0<\theta <\frac{\pi}{2}\) より\(,\) \(\sin{\theta}\neq 0\) であるから\(,\)
\begin{align}2a\cos^2{\theta}-1=0\end{align}
\(a\neq 0\) より\(,\)
\begin{align}\cos^2{\theta}=\frac{1}{2a}\end{align}
\(\displaystyle 0<\theta <\frac{\pi}{2}\) より\(,\) \(\cos{\theta}>0\) であるから\(,\)
\begin{align}\cos{\theta}=\frac{1}{\sqrt{2a}}~~~~\cdots \fbox{答}\end{align}
(2) の解答
\begin{align}\int (a\sin{2x}-\tan{x})dx\end{align}
\begin{align}=-\frac{a}{2}\cos{2x}+\log{|\cos{x}|}+C~~~~\cdots \fbox{答}\end{align}

quandle
\begin{align}\int \tan{x}dx=-\log{|\cos{x}|}+C\end{align}
は要暗記です!もちろん導出の仕方も押さえておきましょう.
\begin{align}\int \tan{x}dx=\int \frac{\sin{x}}{\cos{x}}dx\end{align}
と変形して微分接触形です.
\begin{align}=\int -\frac{(\cos{x})^{\prime}}{\cos{x}}=-\log{|\cos{x}|}+C\end{align}
ですね.
(3) の着眼点
被積分関数に絶対値がついています. \(f(x)\) が正なのか負なのかによって絶対値の外れ方が違います.
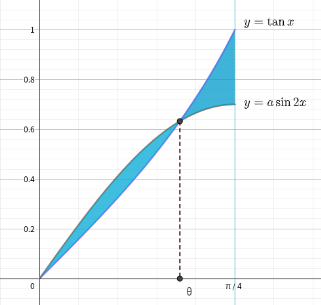
まずは\(,\) \(y=a\sin{2x}\) のグラフと \(y=\tan{x}\) のグラフをかいて上下関係を調べてみましょう.
\(\displaystyle \frac{1}{2}<a<1\) ですから\(,\) \(0<a\sin{2x}<1\) です.
このことを意識しながらグラフをかくとある \(1\) 点で交わることがわかります.
この交点の \(x\) 座標は\(,\) \(a\sin{2x}=\tan{x}\) を満たすはずです.
これはもちろん (1) で求めた \(\theta\) のことですね!
(3) の解答
\(f(x)\) の原始関数の \(1\) つを \(F(x)\) とおく.
\begin{align}\int_0^{\frac{\pi}{4}}|f(x)|dx+\log{a}\end{align}
\begin{align}=\int_0^{\theta}f(x)dx-\int_{\theta}^{\frac{\pi}{4}}f(x)dx+\log{a}\end{align}
\begin{align}=\biggl[F(x)\biggr]_0^{\theta}-\biggl[F(x)\biggr]_{\theta}^{\frac{\pi}{4}}+\log{a}\end{align}
\begin{align}=2F(\theta)-F(0)-F\left(\frac{\pi}{4}\right)+\log{a}\end{align}
\begin{align}=-a\cos{2\theta}+\log{\cos^2{\theta}}-\left(-\frac{a}{2}\right)-\left(-\frac{1}{2}\log{2}\right)+\log{a}\end{align}
\begin{align}=-a(2\cos^2{\theta}-1)+\log{\left(\frac{1}{2a}\right)}+\frac{a}{2}+\frac{1}{2}\log{2}+\log{a}\end{align}
\begin{align}=-a\left(\frac{2}{2a}-1\right)-(\log{2}+\log{a})+\frac{a}{2}+\frac{1}{2}\log{2}+\log{a}\end{align}
\begin{align}=\frac{3}{2}a-\frac{1}{2}\log{2}-1~~~~\cdots \fbox{答}\end{align}


2015年第3問のコピー.jpg)
2021年第3問-120x68.jpg)

コメント